Linear Regression(선형 회귀)

• 데이터의 경향성을 가장 잘 설명하는 하나의 직선을 예측하는 것

Linear Hypothesis

• H(x) = Wx + b

어떤 선, 모델이 우리 가설에 잘 맞을까?
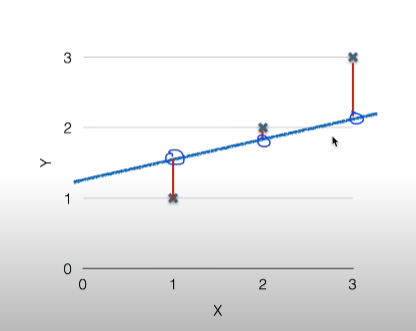
각각의 실제 데이터와 우리의 가설(일차방정식)의 차이가 적을수록 좋음

• 예시
  -국어 성적과 수학 성적, 키와 몸무게, 치킨 판매량과 맥주판매량 같은 2개의 데이터에 대한 경향성 예측

Cost function

• 데이터의 경향성을 가장 잘 설명하는 하나의 직선과 각 데이터의 차이를 잔차라고함
• 실제 데이터와 직선에서 가장 적은 거리값이 뭔지 계산하는 것을 cost function(=loss function)
• so, cost function = how fit the line to our (training) data
• (H(x)-y)^2으로 계산하는데 그 이유는 데이터가 음수 일때 영향을 덜 받을 수 있고 제곱이기때문에 차이가 적을때보다 차이가 클때 패널티를 줄 수 있음

회귀의 목표: cost를 최소화 하는 것

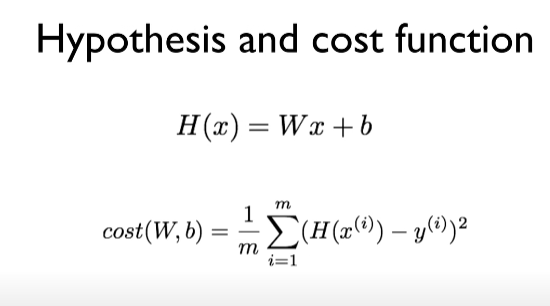
Gradient descent algorithm

• cost funtin 최소화
• 경사 하강 알고리즘은 함수의 기울기(경사)를 구하고 경사의 절댓값이 낮은 쪽으로 계속 이동시켜 극값에 이를때까지 반복시키는 것

어떻게 작용하나?

• 아무 값에서 시작함
• W를 바꿔서 코스트를 줄임
• 경사도를 계산함
• 위의 방법을 반복함
• 경사도를 구하는 법은 미분을 통해서!
  

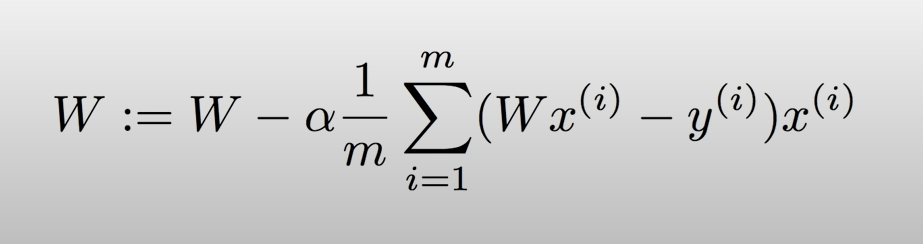
왜 머신러닝에서 쓰일까?

• 실제 분석에서 보게 되는 함수들은 형태가 굉장히 복잡해서 미분계수와 그 근을 계산하기 어려운 경우가 많음
• 미분계수 계산 과정을 컴퓨터로 구현하는 것보다 경사하강법을 구현하는 것이 훨씬 쉬움
• 데이터의 양이 매우 큰 경우에 경사하강ㅂ버과 같은 순차적인 방법이 계산량 측면에서 훨씬 효율적