
순전파
- 입력층에서 입력된 신호가 은닉층의 연산을 거쳐 출력층에서 값을 내보내는 과정
- 입력층, 은닉층, 출력층
- 퍼셉트론: 가중치, 활성화 함수
손실함수
- 예측값이 실제 값과 얼마나 유사한지 판단하는 기준이 필요한데 그게 바로 손실함수
- loss를 줄이는 방향으로 학습진행
분류에 쓰이는 손실함수
1.Binary cross entropy
2.categorical crossentropy(001, 010, 100)
3.sparse_categorical_crossentropy(0,1,2)
*categorical, sparse_categorical 차이: label이 정수일때 원핫 인코딩의 차이
cross entropy

출처: https://stackoverflow.com/questions/41990250/what-is-cross-entropy
실제 분포 q(x)에 대해서 알지 못하는 상황에서 모델링을 통해서 구한 분포인 P(x)를 통해 q(x)를 예측하는 것
그래서 크로스 엔트로피에서 실제값=예측값이면 0으로 수렴하고
실제값=!예측값이면 값이 커진다.
Binary cross entropy: 이진분류에 사용되는 방식
예) true/false, 양성/음성
- 2개의 class를 분류할 때 사용하기 때문데 예측값이 0 또는 1의 값이 나옴
Categorical cross entropy: 분류해야할 클래스가 3개 이상인 경우
- one hot encoding 형태로 사용됨(정답은 1이고 나머지는 모두 0)
- 여러 클래스중 가장 적절한 하나의 class를 분류하는 문제의 손실함수로 사용하기 적합
역전파
- 순전파와 반대방향으로 손실(loss & error) 정보를 전달해주는 과정
- 역전파는 구해진 손실정보를 출력층 => 입력틀까지 전달하고 각 가중치를 얼마나 업데이트 해야할지를 구하는 알고리즘
손실을 줄이는 방법으로 가중치를 계산됨
옵티마이저
경사를 내려가는 방법 결정
- 경사하강법 GD:모든데이터 사용->데이터가 커질수록 느림
- 확률적 경사하강법 SGD: 1개 데이터 사용 -> 빠름/불안정한 경사하강
- 미니 배치 GD: n개 데이터
배치 사이즈: 크면 클수록 안정적, 2의 배수
of data = Batch_size * iteraion
- iteration: 순전파+역전파까지하는것
- 이터레이션이 작으면 역전파의 가중치 업데이트가 낮아지게 됨
- 1에포크: 전체 데이터를 학습
경사하강법(Gradient Decent)
- 가중치의 수정방향을 결정하는 것 즉 손실을 줄이는 방법으로 가중치 업데이트 > 경사하강법
- 가중치 수정 방향을 결정(기울기가 어떻게 생겼냐에 따라 계산이 달라짐)
- 계산 방법은? 손실함수의 미분값(기울기)
- 경사하강법은 함수의 최소값(=미분값)을 찾는 문제에 활용됨
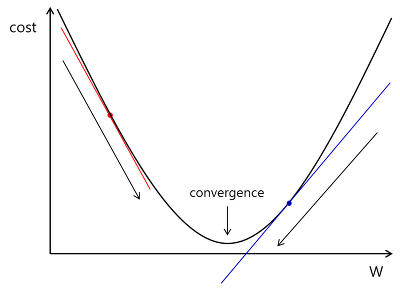
출처:https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=tgif2002&logNo=221488835758
양의 기울기(파랑색)은 기울기 0이 되는 지점으로 가깝게 음의 방향으로 기울기를 줄여나감
음의 기울기(빨간색)은 기울기 0이 되는 지점으로 가깝게 양의 방향으로 기울기를 줄여나감
*기울기가 0이되는 지점은 파란, 빨간 막대가 수평인 모습
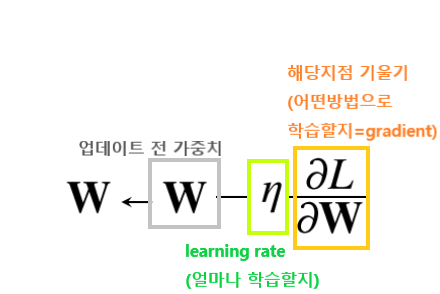
가중치를 수정할때는 weights-(learning*gradient) = new weights 이런 방식으로 진행함
but 경사하강법의 문제점
- 에러를 구할때 전체데이터를 고려해서 구하는데 전체 데이터를 1회 학습했을 때 1epoch라고 부르는데 전체 데이터가 많아지면 전체를 고려해서 한번씩 가중치를 수정해야함
이게 왜 문제냐면?
작은데이터에선 문제되지 않는데 1억건의 데이터를 하나씩 가중치를 수정하는게 시간낭비임
이문제를 해결하기 위해 "확률적 경사 하강법"이 나옴
*로컬 미니멈의 문제도 있긴한데..이건 확률적 경사 하강법에서도 나타나는 문제임 그래서 모델을 다시 돌리던 다른 방향을 모색해야함
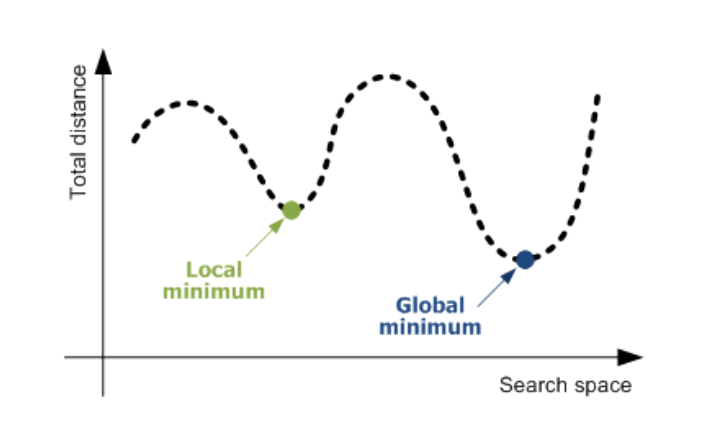
출처: https://wjddyd66.github.io/dl/NeuralNetwork-(3)-Optimazation2/
확률적 경사하강법
- 전체 데이터에서 하나의 데이터를 뽑아서 신경망에 입력한 후 손실을 계산하고 그 손실정보를 역전파해서 신경망의 가중치를 업데이트

출처: https://thebook.io/080263/ch04/02/03-03/장점: 가중치를 빠르게 업데이트 할 수 있음
단점: 불안정한 경사하강
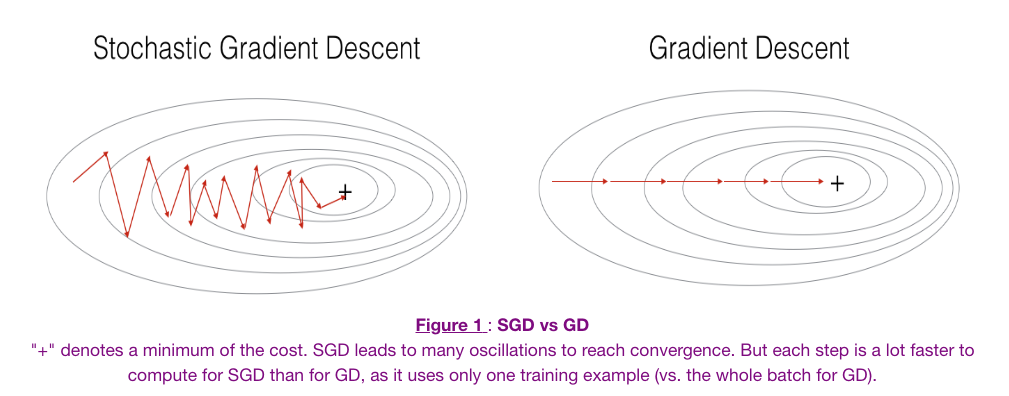
출처: https://yngie-c.github.io/deep%20learning/2020/03/19/training_techs/
그림 오른쪽을 보면 완전 지그재그로 가고 있음= 불안정하게 찾아간다는 것
미니 배치 경사하강법
- 확률적 경사하강법의 단점인 불안정한 경사하강을 해결해줌
- 한개가 아닌 n개의 데이터로 미니 배치를 구성하여 해당 미니 배치를 신경망에 입력한 후 이 결과를 바탕으로 가중치를 업데이트 함
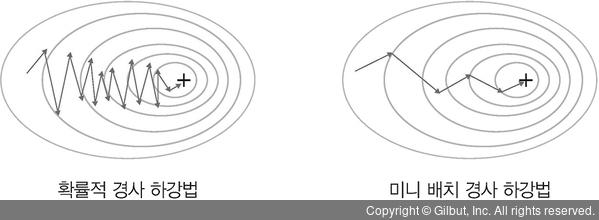
출처: https://thebook.io/080263/ch04/02/03-05/
순전파-손실함수-역전파 일상용어 예시
예시: 공무원 시험 준비 중이고 매뉴얼대로 공부를 했는데 역사에서 점수가 낮게 나왔다.(순전파)
역사의 원래 맞아야하는 점수와 내 점수를 비교했더니 일제강점기 부분에서 많이 틀렸음(손실함수)
일제강점기 부분을 좀더 보완해서 공부하고 시험점수를 높임(역전파)