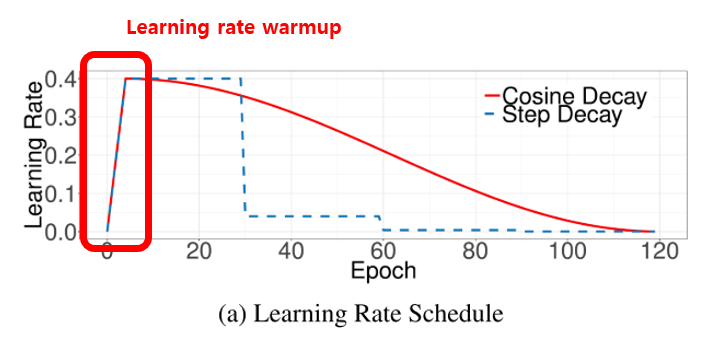
🎯 학습률(Learning Rate)

• 매 가중치에 대해 구해진 기울기 값을 얼마나 경사하강법에 적용할 지 결정하는 하이퍼 파라미터

⏳ 학습률

• 기울기가 감소하는 방향으로 얼마나 이동할지를 조정하는 하이퍼 파라미터(=보폭을 결정)
  
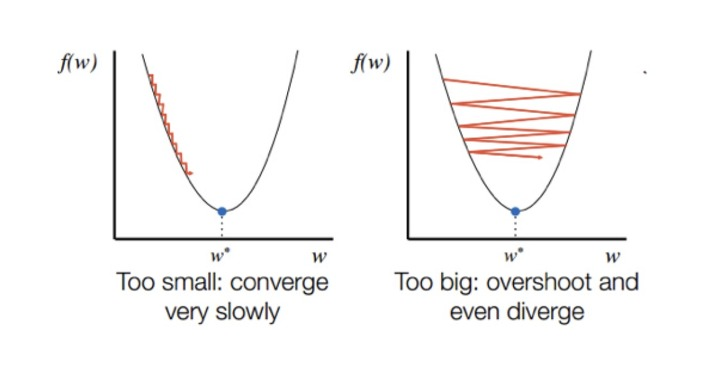
  출처: https://brunch.co.kr/@namujini/23

❓학습률이 너무 낮으면?(왼쪽 그림)

• 최적점에 이르기까지 너무 오래걸림
• 주어진 iteration내에서 최적점에 도달하는데 실패

❓학습률이 너무 높으면?(오른쪽 그림)

• 경사하강과정에서 발산하면서 모델이 최적값을 찾을 수 없게됨

📊 학습률 감소/계획법

1. 학습률 감소(learning rate decay)

• 옵티마이저 적용(adagrad, rmsprop, adam) => .exterminal 내부함수로 설계 가능
• 웜업방식의 학습방법
• 학습률을 높였다가 낮췄다가같이 다양한 학습률로 로컬미니멈을 빠져나오도록 장치하는 방법

출처: https://hoya012.github.io/blog/Bag-of-Tricks-for-Image-Classification-with-Convolutional-Neural-Networks-Review/

코사인 감소(cosine decay)

• 크게 시작하고 작게 만듦
• 일반 선형함수를 사용하기보다 cosine함수를 사용하는 것이 더 좋은 퍼포먼스를 보임

2. 가중치 초기화(weight initialization)_초기 가중치 설정과 관련

• 학습의 성공 유무를 결정하는 중요한 요소
• 옵티마이저: 산을 내려가는 경사를 내려가는 방법
• 가중치 초기화: 산의 어느지점부터 내려갈지 결정하는 방법

⚠️ 만약 잘못된 가중치 초기화를 하면 "역전파 알고리즘 진행간에 2가지 문제가 생긴다.

1. 그래디언트 소실(Vanishing gradient)

• 깊이가 깊은 심층 신경망에서 역전파 알고리즘이 layer를 통해 입력층 방향으로 진행될수록 그래디언트 값이 점점 사라져 가중치 매개변수가 업데이트 되지 않는 현상
  (활성화 함수 출력이 -1, 1로 집중되서 기울기가 0이 된다)

2. 그래디언트 폭주(explioding gradient)

• 매개 변수가 급격히 커지게 되어 학습이 어려운 현상
  ( ReLU는 입력 절대값이 클 경우 문제가 발생한다. 음수면 dead ReLU, 양수면 그래디언트 폭주)

1) 표준 편차를 1인 정규분포로 가중치를 초기화 할때 각 층의 활성화 값 분포

• 잘 사용하지 않음
• 활성화 값이 0,1에 분포 되어있음
  
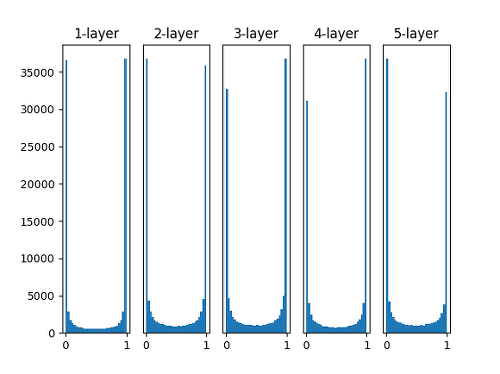
  출처: https://reniew.github.io/13/

2) Xavier 초기화

• 표준편차가 고정값이 정규분포로 초기화 했을때 문제점을 해결하기 위해 등장
• 이전층 노드 n개를 현재층의 가중치를 표준현차가 1/√n인 정규 분포로 초기화함

• keras Xavier는 좀 다름
  : 이전층 노드 n, 현재층의 노드 m 현재층 가중치를 표준편차가 1/√n+m인 정규 분포로 초기화

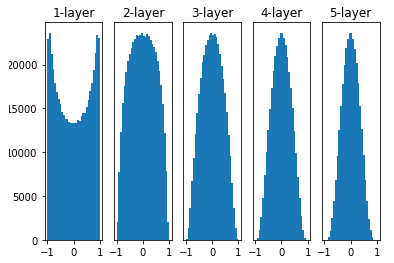
출처: 코드스테이츠

🚫문제점

• 활성화 함수가 시그모이드인 신경망 모델에서 잘 작동한다.
  ReLU에는 층이 지날수록 활성화 값이 고르지 않는다.

3) He 초기화

• 이전층의 노드가 n개 있을때 , 현재층의 가중치를 표준편차가 2/√n
  인 정규분포로 초기화
• ReLU 사용할때 사용

---

🎯 과적합 방지하는 방법

1. Weight Decay(가중치 감소)

• 과적합은 가중치가 클때 주로 발생하기 때문에 가중치 값이 커지지 않게 제약 조건을 추가
  1) L1 regularization(Lasso)
• 가중값의 절댓값의 합
  2) L2 regularization(Ridge)
• 가중값을 제곱 합, 큰 가중치는 크게 낮추고 작은 가중치는 작게 낮춰서 가중치를 균등하게 만들어줌

  커널과 액티비티
  커널 :레이러 가중치에 패널티를 줌=>l2가 좀더 맞음
  액티비티: 레이어 출력에 패널티를 줌=> l1이 좀더 잘 맞음

2. Dropout

• iteration 마다 레이어 노드 중 일부를 사용하지 않으면서 학습을 진행하는 방법
• 매번 다른 노드가 학습되어 과적합을 방지해줌
  
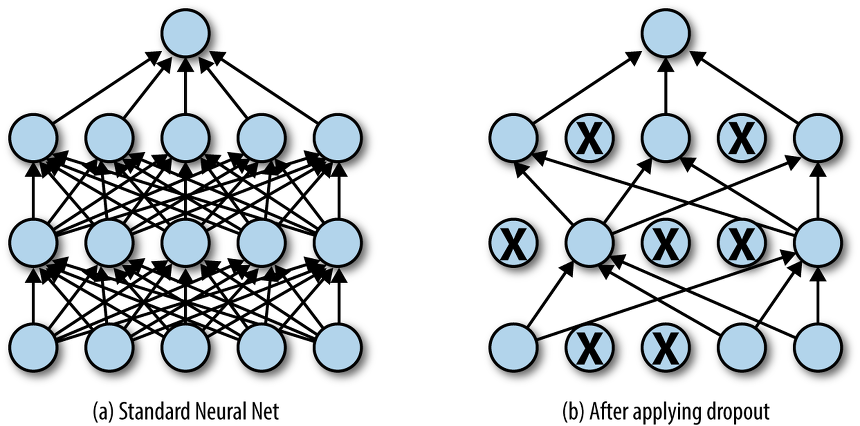
  출처: https://jjeongil.tistory.com/578

3. Early stopping

• 학습데이터에 대한 손실은 계속 줄어들지만 검증 데이터 셋에대한 손실은 증가한다면 학습을 종료
  즉, 검증데이터가 증가하는 시점에서 학습을 멈춰서 과적합을 방지하는 방법