합성곱(convolution)

• 두 함수를 곱해서 합한다

채널(channel)

• 컬러 사진은 각 픽셀을 RGB 3개의 실수로 표현한 3차원 데이터
• 흑백은 2차원 데이터 1개의 채널

필터(filer)

• 커널(kernel)이라고도 함
• 필터는 이미지의 특징을 찾아내기 위한 공용 파라미터
• 학습 대상의 필터 파라미터
• 입력 데이터를 지정된 간격으로 순회하며 채널별로 합성곱을 하고 모든 채널(컬러의 경우 3개)의 합성곱의 합을 피처맵으로 만듦

스트라이드(stride)

• 필터가 입력 데이터를 지정된 간격으로 순회하면서 합성곱을 계산하는데 이때 필터가 순회하는 간격을 stride라고함

패딩(padding)

• 컨볼루션 레이어에 출력 데이터가 줄어드는 것을 방지하는 방법으로 보통 0으로 채워 넣음

피쳐 맵(feature map)

• 입력 데이터를 필터가 순회하여 합성곱을 통해서 만든 출력을 피쳐맵이라고 함
• 입력 데이터가 여러 채널일 경우 필터가 각 채널을 순회하여 합성곱을 계산하고 채널 별 피쳐맵을 만듦, 그리고 각 채널의 피쳐맵을 합산하여 최종 피처맵으로 반환
• 즉, 입력 데이터는 채널 수에 상관없이 필터별로 1개의 피쳐맵을 생성

액티베이션 맵(Activation map)

• 피쳐 맵 행렬에 활성화 함수를 적용한 결과 즉, 컨볼루션 레이어에 최종 출력 결과가 "액티베이션 맵"

풀링 레이어(pooling layer)

convolution layer와 비교해서

• 학습대상의 파라미터가 없음
• 풀링 레이어를 통과하면 행렬 크기 감소
• 풀링 레이어를 통해서 채널 수 변경이 없음

일반적으로 pooling 크기와 stride를 같은 크리로 설정하여 모든 원소가 한번 씩 처리되도록 설정

풀링을 하는 이유

=> output feature map의 모든 데이터가 필요하지 않음

풀링 효과

• 파라미터를 줄여서 네트워크의 표현력이 줄어들어 과적합이 방지됨
• 파라미터가 줄어서 계산이 감소하고 하드웨어에 있는 리소스가 절약되는 동시에 속도가 증가함

Convolution layer의 출력 데이터 크기 산정

• 입력 데이터 높이: H
• 입력 데이터 폭: W
• 필터 높이: FH
• 필터 폭: FW
• stride 크기: S
• 패딩 사이즈: P

출력 데이터 크기 계산

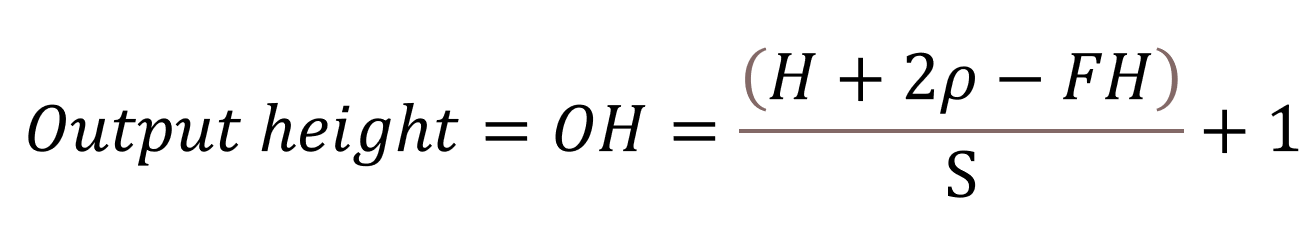
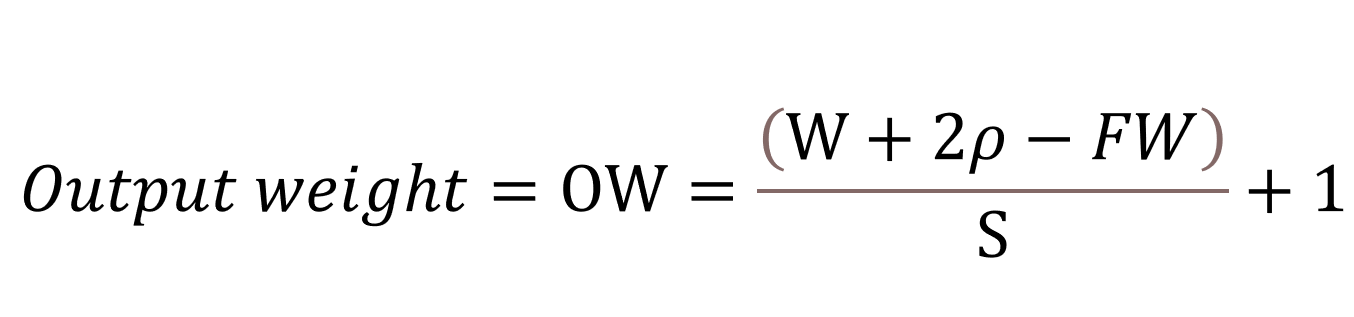
• 식의 결과는 자연수여야함
• convolution layer 다음에 pooling layer가 온다면 피쳐맵의 행, 열크기가 pooling크기의 배수여야함
  ex) 만약 풀링 사이즈가 (3,3)이라면 위 식의 결과느 자연수이고 3의 배수여야함
  즉, 이조건을 만족하도록 필터의 크기, stride의 간격, 풀링 크기 및 패딩크기를 조절

Pooling layer 출력 데이터 크기 산정

• 풀링 사이즈를 stride 같은 크기로 만들어서 모든 요소가 한번 씩 풀링되도록 만듦
• 즉, 풀링 레이어의 출력 데이터의 크기는 행과 열의 크기를 풀링 사이즈로 나눈 몫임
  
  

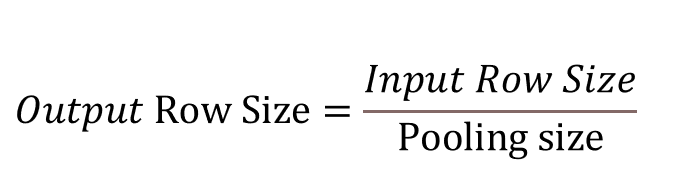
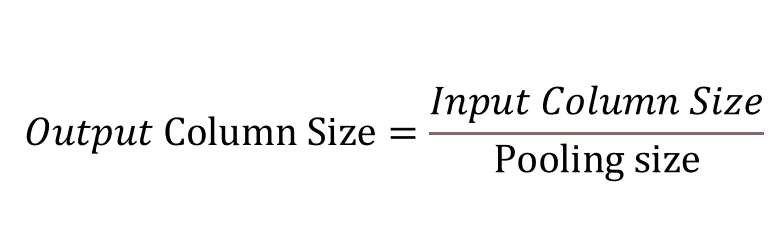
Fully Connected Layer

1. convolution/pooling layer

• 이미지를 형상으로 분할하고 분석

conv layer

• 필터는 이미지를 통과하여 한 번에 몇 픽셀을 스캔하고 각 형상이 속하는 클래스를 예측하는 형상 맵을 만듦

pooling layer

• 가장 중요한 정보를 유지하는 동시에 각 피처의 정보량을 줄임

2. FC layer

• 이미지를 분류/설명 하는데 적합하게 예측

1. 2차원 배열 형태의 이미지를 1차원 배열로 평탄화
2. 활성화 함수(Relu, Leaky Relu, Tanh등) 뉴런을 활성화
3. 분류기(softmax)함수로 분류
   1~3과정을 Fully Connected layer라고 말할 수 있음

개인적으로 헷갈린 것들 정리

• (128,128,3) = (세로 픽셀, 가로 픽셀, 컬러 채널)