문제
처음에 이 문제를 접했을 때에는 dfs를 통해 가능한 모든 경로를 탐색하면서 목적지에 도착할 때마다 ans 값에 +1을 해주어 해당 값을 답으로 출력해주려고 했다.
초기 코드
n = int(input())
graph = [list(map(int,input().split())) for _ in range(n)]
ans = 0
def dfs(a,b):
global ans
dx = [1,0]
dy = [0,1]
for i in range(2):
nx = a + dx[i]*graph[a][b]
ny = b + dy[i]*graph[a][b]
if 0<=nx<n and 0<=ny < n:
if graph[nx][ny] == 0:
ans += 1
else:
dfs(nx,ny)
else:
continue
dfs(0,0)
print(ans)이렇게 해서 테스트케이스에 대한 답은 출력했지만 시간초과라는 문제가 발생했다.
아무리 생각해도 dfs로 푸는 문제같은데 시간초과가 발생하여 당황스러웠다..
그래서 구글링을 해본결과 대부분의 사람들이 dp를 통해 이 문제를 해결해주었다는 것을 알게되었다.
dp로 해결해볼 생각은 못해봤는데....
아무튼 dp를 적용하여 문제를 해결 해준 코드는
정답 코드
n = int(input())
graph = [list(map(int,input().split())) for _ in range(n)]
ans = 0
dp = [[0]*n for _ in range(n)]
dp [0][0] = 1
def sol():
for i in range(n):
for j in range(n):
k = graph[i][j]
if k == 0 or dp[i][j] == 0:
continue
#아래쪽으로 이동하는 경우
if i + k < n:
dp[i+k][j] += dp[i][j]
#오른쪽으로 이동하는 경우
if j+k < n :
dp[i][j+k] += dp[i][j]
return dp[-1][-1]
print(sol())이렇게 해결 해주었다.
dp를 통해서 갈 수 있는 경로 마다 경우의 수를 더해주면서 체크해주는 방법이다
그리고 이때 시작지점을 1로 해주고 (0,0) 인 시작지점에서 갈 수 있는 곳의 dp를 1로 바꾸어주면 계속해서 해당 좌표에서 갈 수 있는 경로에 해당되는 좌표만 더해지게 되는 것이다
그러므로 dp가 0인부분은 점프 규칙상 도달할 수 없는 곳이므로 제외처리를 해주면 된다. 물론 목적지에 도달했을 때도 더이상 계산할 것이 없으므로 같이 제외처리 해주면된다.
그리고 (i,j) 좌표에서 주어진 수에 해당되는 만큼 오른쪽이나 아래쪽으로 갈 수있는 좌표에 해당되는 부분은 dp를 더해주어 이 좌표가 몇개의 경로에 포함되는 지를 계산해주는 것이다.
dp[-1][-1] 을 return 해주는 이유는 dp의 해당 좌표(목적지)에 몇개의 경우의 수로 갈 수 있는 지가 저장되어있기 때문이다.
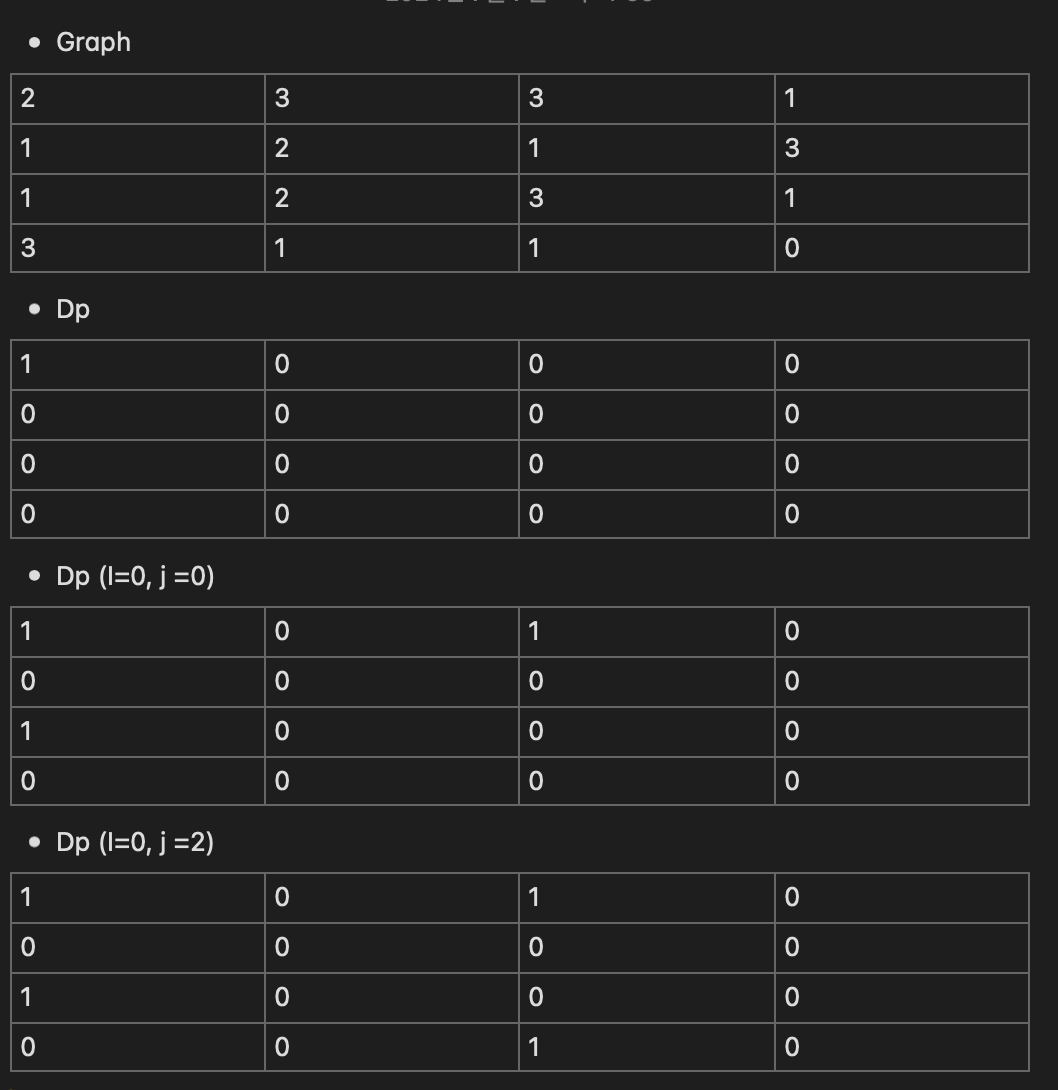
그림으로 설명해보자면 이렇게 된다.
계속 해서 규칙에 따라 갈 수 있는 좌표에 해당 좌표가 몇개의 경로에 포함되는 지를 dp에 저장해주는거라고 보면 된다.
