자료구조의 개념
1.컴퓨터 시스템
(1) 시스템의 정의
컴퓨터 언어에서는 다양한 자료를 보다 효율적으로 처리하기 위해 자료형(data type)이라는 개념을 사용하는데, 자료형에는 문자형, 정수형, 실수형, 복소수형, 레코드형, 구조체형 등이 제공되는데, 언어에 따라 지원되는 자료형의 종류와 자료를 취급하는 방법은 약간의 차이가 있다.
(2) 시스템의 구성 요소
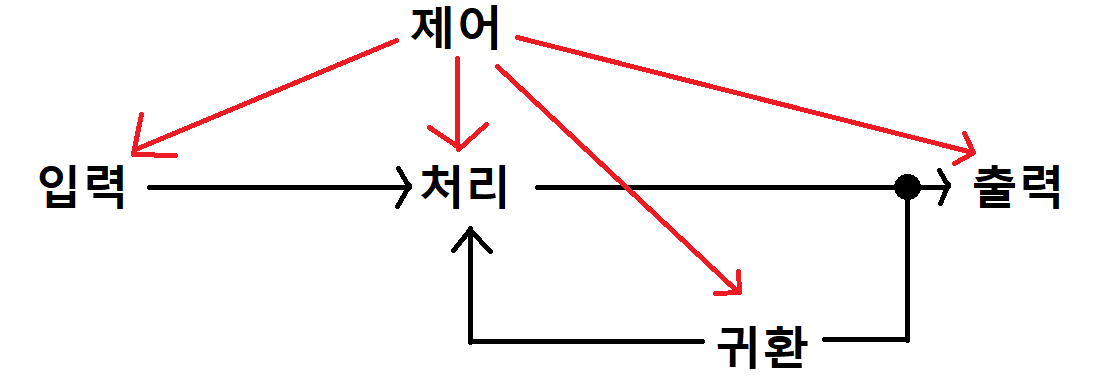
- 입력(input): 처리할 자료 및 처리 방법을 시스템 안으로 입력한다.
- 처리(processing): 입력된 자료와 처리 방법에 따라 자료를 가공한다.
- 출력(output): 처리된 결과를 와부로 출력
- 제어(control): 시스템의 목적을 달성하기 위한 모든 과정을 제어한다.
- 귀환(feed back): 처리된 결과를 다시 입력 자료로 사용한다.
2.자료와 정보
(1) 정의

I = P(D) [I(Information), P(Process), D(Data)], 데이터는 정보와 같지 않다.
정보가 유용성을 갖기 위해서는 정확성과 현재성을 갖고 있어야 함.
(2) 자료(Data)
- 현실 세계로부터 단순한 관찰이나 츠정을 통해서 수집된 사실이나 값이다.
- 사람이나 컴퓨터가 인식하고 처리하는 데 알맞은 형태로 존재하며, 평가되진 않는다.
- 원시적이고 처리되지 않은 사실이나 통계이다. 이것들 자체로는 큰 의미가 없다.
(3) 정보(information)
1.자료가 처리되어 특정 문맥에서 유용하게 사용될 수 있는 형태이다. 정보는 의사결정에 도움이 되도록 설계되어야 한다.
2.어떤 상황에 대한 적절한 의사 결정을 할 수 있게 하는 데이터의 유효한 해석(interpretation)이나 상호관계(relationship)이다.
- 발전 단계: Data → Informatin → Knowledge → Intelligence
3. 자료의 단위
(1) 비트(bit)
- 0 또는 1을 의마하는 자료의 최소 단위이다. binary digit의 약어이다.
- 하나의 비트는 서로 다른 2가지 종류의 데이터만을 표현할 수 있다.
- 컴퓨터는 내부적으로 2진수로 데이터가 처리된다.
(2) 니블(nibble)
- nibble은 4비트를 의마한다.
- 10진수 한 자리를 표현하는 단위로 사용할 수 있다.
(3) 바이트(byte)
- 8bit의 한 묶음으로 1문자를 나타낸다.
- 하나의 문자를 나타낼 수 있는 단위
(4) 워드(word)
- CPU에서 처리되는 명령의 단위이다.
- half word = 2bytes, full word = 4bytes, double word = 8bytes 등으로 나뉜다.
- 컴퓨터에서 자료가 연산되는 단위로, 컴퓨터가 한번에 처리할 수 있는 자료의 양을 의미한다.
- 컴퓨터의 모든 명령은 기본적으로 워드 단위로 수행된다. 워드 길이는 CPU를 구성하는 레지스터 크기와 같다. 64비트 컴퓨터는 CPU가 한꺼번에 64비트씩 처리할 수 있는 컴퓨터이다.
(5) 필드(field) 또는 항목(item)
- 레코드를 구성하는 항목으로 파일(file)을 구성하는 단위 중 최소의 논리적 단위
- 같은 종류의 data가 기록되는 항목으로 최소한의 문자집합
- 필드는 데이터베이스 테이블의 열(column)을 구성하는 요소로, 특정한 유형의 데이터(예: 이름, 나이, 주소 등)를 포함하고 있다. 각 필드는 일반적으로 데이터베이스 내의 각 레코드에서 특정한 값을 갖게 된다.
- 예를 들어, '학생'이라는 테이블이 있다면, 그 테이블의 각 필드는 '학번', '이름', '학년', '학과' 등을 나타낼 수 있다. 이때 '학번' 필드에는 학번에 해당하는 값들, '이름' 필드에는 이름에 해당하는 값들이 저장되는 것이다.
(6) 레코드(record)
- 서로 관련된 field또는 item의 집합으로 프로그램 상에서 자료의 처리 및 기록 단위 → 논리적 단위, 내부에서 처리되는 단위이다.
- 필드의 집합으로 데이터베이스에서 실제로 정보를 처리할 때 기본이 되는 단위
- 배열은 데이터 원소의 크기와 데이터 타입이 동일한 반면, 레코드는 데이터 원소의 크기와 데이터 형(타입)이 서로 다르다.
- 레코드는 데이터베이스 테이블의 행(row)을 구성하는 요소로, 특정 항목에 대한 모든 필드의 값을 포함하고 있다. 간단히 말해, 레코드는 관련된 여러 필드들의 집합이라고 볼 수 있다.
- 앞서 들었던 '학생' 테이블 예제를 계속 사용한다면, 각 레코드는 한 학생에 대한 모든 정보(학번, 이름, 학년, 학과 등)를 포함하게 될 것이다.
이처럼 필드는 데이터의 유형이나 카테고리를 정의하는 반면, 레코드는 그러한 카테고리에 따라 분류된 개별 데이터를 나타낸다. 이 둘은 데이터베이스에서 데이터를 조직화하고 관리하는 데 중요한 역할을 한다.
(7) 파일(file)
물리적 구조가 같은 레코드의 집합으로 기억매체에 저장되는 단위가 같다.
(8) 데이터베이스(database)
여러 응용 분야에서 여러 사람들이 공동으로 사용할 수 있도록 조작 관리되고 있는 자료의 모임이다.
자료 단위
- bit → byte → word → record → block → file → database → data bank
- bit → byte → field(item) → record → file → database → data bank
용량 단위
- bit → byte → KB → MB → GB → TB
연산 속도 단위
- (느림)ms → μs → ns → ps → fs → as(빠름)
4. 데이터 구조
(1) 정의
- 데이터 객체에 적용될 연산(operation)의 종류와 기능을 결정하고, 그 연산이 실제로 어떻게 이루어지는가를 기술함으로써 데이터 구조가 정의된다.
- 수학적인 모델 또는 논리적인 모델을 컴퓨터 내부에 표현하는 것이다.
- 컴퓨터 기억공간에서 자료처리를 위한 데이터의 표현법, 자료간의 상호 관계를 파악하여 작업을 수행하기 위한 알고리즘을 연구하는 학문이다.
자료구조
자료구조란, 컴퓨터에서 처리할 데이터를 효율적으로 저장하고 관리하는 방법을 말한다. 여기서 '효율적'이란 데이터를 처리하는데 필요한 시간과 공간을 최소화하는 것을 의미한다.
- 스택(Stack): 스택은 마지막에 들어간 데이터가 먼저 나오는 LIFO(Last In, First Out) 구조를 가진다. 스택에 데이터를 넣는 것을 'push', 꺼내는 것을 'pop'이라고 한다. 스택은 함수 호출, 괄호 검사, 후위 표기법 등에서 사용된다.
- 큐(Queue): 큐는 먼저 들어간 데이터가 먼저 나오는 FIFO(First In, First Out) 구조를 가진다. 큐에 데이터를 넣는 것을 'enqueue', 꺼내는 것을 'dequeue'라고 한다. 큐는 너비 우선 탐색, CPU 스케줄링, 대기열 관리 등에서 사용된다.
- 리스트(List): 리스트는 순차적인 데이터를 저장하며, 각 요소는 다음 요소를 가리키는 방식으로 연결되어 있다. 리스트는 단일 연결 리스트(Singly Linked List), 이중 연결 리스트(Doubly Linked List), 원형 연결 리스트(Circular Linked List) 등 여러 종류가 있다.
- 그래프(Graph): 그래프는 노드와 그 노드들을 연결하는 간선으로 이루어진 구조다. 그래프는 연결된 요소 간의 관계를 모델링하는 데 사용되며, 사회 네트워크, 웹 페이지의 링크 구조, 도로 네트워크 등 다양한 상황에서 사용된다.
- 트리(Tree): 트리는 노드들이 계층적으로 연결된 그래프 구조다. 각 노드는 자식 노드를 가질 수 있고, 한 개의 부모 노드를 가진다. (단, 루트 노드는 부모 노드가 없다.) 트리는 파일 시스템, HTML 문서의 DOM, 데이터베이스 관리 등에서 사용된다. 특히, 이진 트리(binary tree)는 컴퓨터 과학에서 매우 중요한 자료 구조로, 효율적인 검색과 정렬에 활용된다.
| 일상생활에서의 예 | 해당하는 자료구조 |
|---|---|
| 그릇을 쌓아서 보관 | 스택 |
| 마트 계산대 줄 | 큐 |
| 버킷 리스트 | 리스트 |
| 지도 | 그래프 |
| 컴퓨터의 디렉토리 구조 | 트리 |
(2) 자료의 형태에 따른 분류
1.단순 구조: 정수, 실수, 문자, 문자열 등의 기본 자료형
2.선형 구조: 자료들 간의 앞뒤 관계가 1:1의 선형관계
예) 리스트, 연결리스트, 스택, 큐, 데크 등
3.비선형 구조: 자료들 간의 앞뒤 관계가 1:다, 또는 다:다의 관계
예) 트리, 그래프 등
4.파일 구조: 레코드의 집합인 파일에 대한 구조
예) 순차파일, 색인파일, 직접파일 등
선형구조
-
배열(Array): 배열은 같은 유형의 데이터를 순차적으로 저장하는 가장 기본적인 자료 구조이다. 각 요소에는 인덱스를 통해 접근할 수 있으며, 모든 요소는 메모리 상에서 연속적인 위치에 저장된다. 배열의 크기는 생성 시 결정되며, 그 후에는 변경할 수 없다. (물리적 연속성, 검색연산↑, 기록밀도↑, 수정연산↑, 삼입·삭제연산↓, 정적구조, 외부단편화 발생)
-
연결 리스트(Linked List): 연결 리스트는 각 요소가 다음 요소를 가리키는 포인터를 가지고 있는 선형 자료 구조이다. 배열과 달리 연결 리스트의 요소들은 메모리 상의 임의의 위치에 저장될 수 있다. 연결 리스트는 노드의 추가 및 삭제가 자유롭지만, 특정 인덱스에 있는 요소에 접근하려면 첫 노드부터 순차적으로 접근해야 한다. (논리적 연속성, 검색연산↓, 기록밀도↓, 수정연산↑, 삼입·삭제연산↓, 동적구조, 외부단편화 미발생)
비선형 구조
-
트리(Tree): 트리는 계층적인 자료 구조로, 각 노드가 두 개 이하의 자식 노드를 가지는 경우를 일반적으로 가리킨다. 트리의 노드는 부모-자식 관계를 가지며, 루트(root) 노드에서 시작해서 잎(leaf) 노드로 뻗어나갑니다. 트리는 이진 트리, B-트리, 힙 등 다양한 형태가 있다. (사이클 허용하지 않음, 그래프의 특수한 형태)
-
그래프(Graph): 그래프는 노드들이 간선을 통해 서로 연결된 비선형 구조다. 그래프는 순환적인 구조(사이클 허용)를 가질 수 있으며, 하나의 노드가 여러 개의 노드와 연결될 수 있다. 그래프는 방향성을 가질 수도 있고(방향 그래프) 가지지 않을 수도 있다(무방향 그래프).
각 자료 구조는 서로 다른 특징과 장단점을 가지며, 이에 따라 상황에 맞는 자료 구조를 선택하는 것이 중요하다.
- 검색연산(Search Operation): 검색 연산은 주어진 집합에서 특정한 값을 찾는 연산이다. 예를 들어, 배열에서는 인덱스를 사용하여 O(1)의 시간 복잡도로 원하는 값을 찾을 수 있다. 반면에 연결 리스트에서는 원하는 값을 찾기 위해 처음부터 끝까지 탐색해야 하므로 최악의 경우 O(n)의 시간 복잡도를 가진다.
- 기록밀도(Record Density): 기록 밀도는 데이터 저장 공간에 대한 효율성을 나타낸다. 배열은 고정된 공간을 할당받아 사용하기 때문에 메모리 사용이 효율적이다. 하지만 연결 리스트는 각 노드에 대한 포인터 공간이 추가로 필요하므로, 같은 수의 데이터를 저장할 경우 배열에 비해 더 많은 메모리 공간을 차지한다.
- 수정연산(Modify Operation): 수정 연산은 자료 구조에 저장된 데이터를 변경하는 연산이다. 배열과 연결 리스트 모두 특정 위치의 값을 수정하는 연산은 O(1)의 시간 복잡도를 가진다. 하지만, 배열에서는 크기 변경이 불가능하기 때문에 배열의 크기를 변경하려면 새 배열을 만들어 모든 데이터를 복사해야 한다.
- 삽입삭제연산(Insertion and Deletion Operation): 삽입 및 삭제 연산은 자료 구조에 데이터를 추가하거나 제거하는 연산이다. 배열에서는 삽입 또는 삭제를 위해 모든 데이터를 이동해야 하므로 O(n)의 시간 복잡도를 가진다. 반면에 연결 리스트에서는 삽입 및 삭제가 O(1)의 시간 복잡도로 이루어진다. (단, 삭제를 위해선 탐색이 필요하므로 실제로는 O(n)의 시간 복잡도를 가진다)
- 정적구조(Static Structure) vs 동적구조(Dynamic Structure): 정적 구조는 자료 구조의 크기가 고정되어 있고, 실행 중에 변경할 수 없는 구조를 말한다. 배열이 이에 해당한다. 반면에 동적 구조는 실행 중에 크기가 변할 수 있는 구조로, 연결 리스트가 이에 해당한다.
- 외부단편화(External Fragmentation): 외부 단편화는 메모리가 연속적인 블록으로 할당될 때 발생하는 현상이다. 메모리의 여러 부분에 빈 공간이 흩어져 있어, 총량은 충분하지만 이들을 합치지 않으면 큰 블록을 할당할 수 없는 상황을 말한다. 배열을 사용하면 이러한 외부 단편화가 발생할 수 있다. 반면에 연결 리스트는 메모리의 임의 위치에 노드를 할당할 수 있으므로 외부 단편화를 피할 수 있다.
(3) 자료구조 선택 시 고려사항
- 데이터 양과 접근 빈도(access frequency), 접근시간(access time)
- 데이터 성격(잦은 변경을 요구하는 데이터인가?, 일정한 형태를 유지하는가?)
- 사용되는 컴퓨터의 기억장치 용량(메모리 허용도)
- 프로그램 작성의 용이성
- 데이터의 사용 빈도 · 저장방식
(4) 데이터 객체
- 프로그래밍 언어에서 자료를 표현할 때는 정수형, 실수형, 문자형 등으로 자료형을 정의하고 이에 맞는 변수를 사용
- '데이터 객체'는 자료형의 실체를 구성하는 원소의 집합이다.
예) 자연수 N의 데이터 객체 = { 1, 2, 3, 4, 5, 6, .....}
정수형 D의 데이터 객체 = { ..., -3, -2, -1, 0, +1, +2, +3, ...}
추상 데이터 타입(ADT)
1. 추상 데이터 타입(Abstract Data Type, ADT)
(1) 정의
- 데이터 타입(data type)은 객체(object)와 그 객체 위에 작동하는 연산(operation)의 집합이다. 추상 데이터 타입(ADT, abstract data type)은 객체의 명세와 그 연산의 명세가 그 객체의 표현과 연산의 구현으로부터 분리된 데이터 타입이다.
- 어떤 프로그래밍 언어에서는 명세와 구현 사이를 구별하는 기법을 명시적으로 제공함. 예를 들어, Ada에는 package라는 개념이 있고, C++에는 class라는 개념이 있다. 이들 모두 프로그래머가 추상 데이터 아입을 구현하는 것을 돕는다.
- C언어에서는 추상 데이터 타입을 명시적으로 구현하는 기법을 갖지는 않지만, 같은 개념을 사용해서 데이터 타입을 설계하는 것은 가능하고 바람직함.
- ADT연산의 명세는 그 연산의 구현과 어떻게 다른가? 명세는 모든 함수의 이름, 그 함수의 매개변수 타입, 그리고, 함수의 결과 타입으로 구성된다. 그리고 함수가 수행하는 기능에 대한 기술이 있어야 한다.
- 그러나 내부적인 표현이나 구현의 독립에 대한 자세한 설명은 필요 없다. 이러한 요건들은 매우 중요하며, 이것은 추상 데이터 타입이 구현에 독립적임을 의미한다.
- 데이터의 표현이나 연산의 구현은 제외하고 데이터와 연산의 본질에 대한 명세만 정의하는 것이다.
추상화와 추상 데이터 타입
-
추상화(Abstraction): 추상화는 복잡한 시스템을 더 간단하고 이해하기 쉬운 개념으로 변환하는 과정입니다. 이는 불필요한 세부 정보를 숨기고 중요한 정보에만 초점을 맞추는 것을 의미한다. 프로그래밍에서 추상화는 코드의 복잡성을 관리하고, 유지 관리를 간편하게 하며, 코드의 재사용성을 높이는 데 도움이 된다.
-
추상 데이터 타입(Abstract Data Type, ADT): 추상 데이터 타입(ADT)는 추상화 개념을 데이터 구조에 적용한 것이다. ADT는 데이터와 그 데이터에 적용할 수 있는 연산들을 정의하지만, 데이터의 구현이나 연산의 구체적인 알고리즘은 명시하지 않는다. 이렇게 하면 프로그래머는 세부 구현에 신경 쓰지 않고도 데이터 타입을 효과적으로 사용할 수 있다.
예를 들어, 스택 ADT는 스택의 개념을 정의한다. 스택의 ADT는 "push", "pop", "peek", "is_empty"와 같은 연산을 포함하지만, 이 연산들이 어떻게 구현되는지, 즉 데이터가 배열이나 연결 리스트 등으로 구현되는지는 정의하지 않는다. 이렇게 ADT는 사용자가 구현 세부 사항에 신경 쓰지 않고도 데이터 구조를 효과적으로 사용할 수 있도록 한다.
(2) 특징
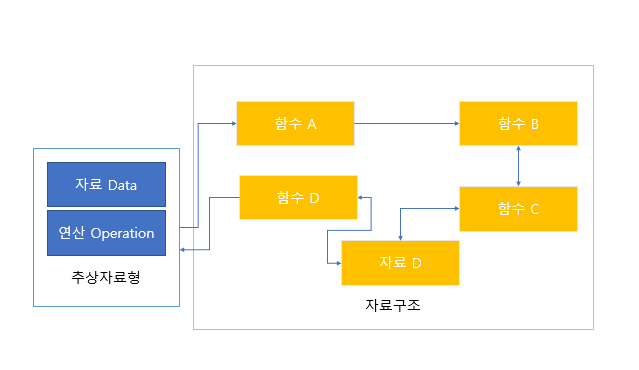
- 추상 자료형은 복잡한 자료형을 정의할 때, 복잡한 세부 구현 내용은 생략하고, 앞으로 변경될 가능성이 적은 대표적이면서도 핵심적인 내용만을 간략히 기술한다. 즉, 추상 자료형은 각 연산이 어떤 기능을 하며 입력값과 출력값이 무엇인지만을 노출하고 있고, 연산 내부의 세부적이고 복잡한 것을 생략하고 있다.
- 이러한 추상 자료형의 특성과 추상 자료형과 자료구조와의 관계를 그림으로 나타내면 다음과 같다
(3) 조건
- 자료형과 연산에 대한 정의가 한 곳에서 가능
- 자료형과 연산이 하나로 묶인 자료형에 대한 프로그램의 접근을 제한할 수 있어야 한다.
(4) 구현 방법
- 자료와 그에 관련된 연산들의 기본적인 특징을 기술
- 이미 존재하는 자료형을 이용하여 기술된 내용을 구현
- 기술 내용과 구현 결과가 일치함을 확인한다.
추상(abstraction) & 연산에 필요한 추상
- 추상화는 복잡한 문제나 시스템을 더 간단하고 이해하기 쉬운 형태로 만드는 과정입니다. 이는 다양한 세부 정보 중에서 중요하고 공통적인 부분만을 추출하여 문제를 단순화하는 작업이라고 할 수 있다.
- 예를 들어, 만약 자동차를 운전한다고 생각해 보자. 자동차의 동작 원리를 완벽하게 이해하지 못하더라도, 여러분은 스티어링 휠을 돌리면 차가 방향을 바꾸고, 페달을 밟으면 차가 움직이거나 멈추는 것을 알고 있다. 이처럼 운전자는 자동차의 동작 원리에 대한 "추상화"를 이해하고 있고, 이를 통해 복잡한 기계를 운전할 수 있다.
- 컴퓨터 과학에서 이 개념은 함수나 객체 지향 프로그래밍의 클래스, 추상 데이터 타입 등에 적용된다. 함수를 사용할 때, 우리는 함수가 무엇을 하는지 (즉, 함수의 입력과 출력이 무엇인지) 알지만, 그 함수가 어떻게 그 결과를 계산하는지에 대해서는 몰라도 된다. 이것이 바로 '연산에 필요한 추상'이라는 개념이다. 우리는 연산의 결과에만 초점을 맞추며, 그 연산이 어떻게 수행되는지는 상세히 알지 못해도 그 연산을 사용할 수 있다. 이러한 추상화는 코드의 복잡성을 관리하고, 코드를 더 이해하기 쉽게 만드는데 중요한 역할을 한다.
- 즉, 연산에 필요한 추상이란 무엇(what)이 수행되는지는 알지만 어떻게(how) 수행되는지는 몰라도 좋다는 것이다.
(5) 추상 데이터 타입(ADT)의 구성 요소
1.구조 이름
2.객체(data)의 정리
3.함수(연산)의 정리
- 데이터 구조는 크기 3부분으로 나눌 수 있다. S = (D, F, A)
- 여기서, S는 표현하려는 데이터 구조, D는 데이터 구조의 정의영역(domain) 집한, F는 함수의 집합으로 데이터 구조에 적용되는 연산의 종류이며, A는 공리(axiom)의 집합으로 연산을 의미한다. 그리고 S와 D는 S∈D의 관계가 된다.
4.NaturalNumber 추상 데이터 타입 예시
ADT NaturalNumber
objects: 0에서 시작해서 컴퓨터상의 최대 정수 값(INT_MAX)까지 순서화된 정수의 부분 범위이다.
functions:
Nat_Number의 모든 원소x, y 그리고 Boolean의 원소
TRUE, FALSE에 대해, 여기서 +,-,< 그리고 ==는 일반적인 정수 연산자이다.
NaturalNumber Zero() ∷= 0
Boolean IsZero(x) ∷= if(x) return FALSE
else return TRUE
Boolean Equal(x,y) ∷= if(x==y) return TRUE
else return FALSE
NaturalNumber Successor(x) ∷= if(x==INT_MAX) return x
else return x + 1
NaturalNumber Add(X,y) ∷= if((x+y)<=INT_MAX) return x + y
else return INT_MAX
NaturalNumber Subtract(x,y) ∷= if(x<y) return o
else return x - y알고리즘과 복잡도
1.알고리즘(Algorism)
(1)정의
- 알고리즘이란 특정한 일을 수행하는 명령어들의 유한 집합이며, 주어진 문제를 하결하기 위한 수행과정을 논리적으로 표현한 것이다.
- 알고리즘은 간단히 말해 어떤 값이나 값의 집합을 입력으로 받아 또 다른 값이나 값의 집합을 출력하는 잘 정의된 계산 절차를 말한다. 따라서 알고리즘은 어떤 입력을 어떤 출력으로 변환하는 일련의 계산 과정이라 할 수 있다.
- 알고리즘은 주로 추상 데이터 타입을 처리하는 반면에 프로그램은 완전히 잘 정리된 데이터 타입만을 처리한다.
- 수행해야 할 작업의 내용과 순서가 명령문으로 완전하고 명확하게 명세되어야 한다.
- 순수하게 알고리즘이 지시하는 그대로 실행하기만 하면 의도한 결과가 얻어져야 한다.
(2)알고리즘의 표현 방법
- 알고리즘에는 입력은 없어도 되지만 출력은 반드시 하나 이상 있어야 하고, 모소한 방법으로 기술된 명령어들의 집합은 알고리즘이라 할 수 없다.
- 또한 실행할 수 없는 명령어(예를 들면 0으로 나누는 연산)를 사용하면 역시 알고리즘이 아니고, 무한히 반복되는 명령어들의 집합또한 알고리즘이 아니다.
- 알고리즘을 기술하는 데는 다음과 같은 4가지 방법이 존재한다.
㉠한글이나 영어같은 자연어: 자연어로 알고리즘을 설명하는 것은 가장 간단하고 직관적인 방법이다. 하지만 자연어는 모호성이 있고, 이해하기에 따라 해석이 달라질 수 있으므로, 정밀한 알고리즘 표현에는 한계가 있다.
㉡의사코드(Pseudocode):의사코드는 일반적인 프로그래밍 언어의 형식을 따르지만, 실제로 컴퓨터에서 실행할 수 있는 코드는 아닌 형태로 알고리즘을 표현하는 방법이다. 의사코드는 알고리즘의 논리를 명확하게 표현하면서도 구체적인 프로그래밍 언어의 문법에 얽매이지 않기 때문에 알고리즘을 이해하고 설계하는 데 유용하다.
㉢흐름도:흐름도는 알고리즘의 각 단계를 도형으로 표현하고, 이 도형들 사이의 흐름을 화살표로 나타내는 방법이다. 흐름도는 알고리즘의 실행 흐름을 시각적으로 표현하므로 이해하기 쉽지만, 복잡한 알고리즘에는 적합하지 않을 수 있다.
㉣형식 언어(Formal Language): 알고리즘을 정확하게 표현하기 위해 특정 프로그래밍 언어나 수학적 언어를 사용하는 방법이다. 이 방법은 알고리즘이 실행될 실제 환경을 반영하므로 정확성과 효율성을 검증하는 데 유용하지만, 특정 언어에 대한 이해가 필요하다.
(3) 요구 조건
- 입력(input): 외부에서 제공되는 데이터가 0개 이상 있다.
- 출력(output): 적어도 하나의 결과를 생성한다.
- 명확성(definition): 각 명령들은 명확하고 모호하지 않아야 한다.
- 유한성(finiteness): 알고리즘의 명령대로 수행하면, 어떤 경우에도 한정된 수의 단계 뒤에는 반드시 종료한다.
→ 프로그램은 반드시 유한성 조건을 만족하는 것이 아니다. 이러한 무한한 프로그램의 한 예로서 운영 체제를 들 수 있다. 운영 체제는 시스템 붕괴하기 전에는 종료하지 않고 다른 작업이 입력될 때 까지 대기 루프를 돌고 있다. - 유효성(effectiveness): 원칙적으로 모든 명령들은 종이와 연필만으로 수행될 수 있게 기본적이어야 한다. 이것은 각 연산이 명확하기만 해서는 안 되고, 반드시 실행 가능해야 한다.
(4) 분석 기준
- 작업량(작업 수행량): 알고리즘을 수행하는 데 걸리는 수행횟수(최선, 최악, 펑균)
- 점유공간의 크기(소요 공간): 차지하는 메모리의 양을 측정
- 단순성(simplicity): 알고리즘 표현의 용이성
- 정확성(correctness): 알고리즘의 논리적 정확도를 측정
- 최적성(optimality): 실행시간의 평균과 최악이 같을 때
2.알고리즘의 복잡도(성능 분석)
(1) 정의
- 프로그램의 공간 복잡도(space complexity)는 프로그램을 실행시켜 완료하는데 필요로 하는 공간의 양이다. 프로그램의 시간 복잡도(time complexity)는 프로그램을 실행시켜 완료하는데 필요한 컴퓨터의 시간의 양을 의미한다.
- 수행시간은 작업 시간에서 완료까지 수행에 걸리는 시간으로 짧을수록 성능이 우수하다.
- 자원의 점유는 프로그램 수행에 필요한 자원의 양으로 점유량이 적을수록 우수하다.
(2) 알고리즘 복잡도와 종류
1) 공간 복잡도(space complexity)
- 프로그램 실행에 필요한 메모리의 양으로 표현한다.
- 프로그램이 필요로 하는 공간은 고정 공간과 가변 공간 요소의 합이 된다.
㉠ 고정 공간 요구: 프로그램 입출력의 횟수나 크리와 관계없는 공간 요구를 의미한다. 고정 공간 요구는 명령어 공간(코드 저장을 위한 공간), 단순 변수, 고정 크기의 구조화 변수(struct과 같은), 그리고 사수들을 위한 공간을 포함한다.
㉡ 가변 공간 요구: 이는 풀려는 문제의 특정 인스턴스 I에 의존하는 크기를 가진 구조화 변수들을 위해 필요로 하는 공간들로 구성된다. 이것은 함수가 순환 호출을 할 경우 요구되는 추가 공간을 포함한다. - 프로그램의 공간 복잡도를 분석할 때는 보통 가변 공간 요구에 대해서만 관심을 둔다. 이것은 특히 여러 프로그램의 공간 복잡도를 비교하려 할 때 유효하다.
공간 복잡도를 분석할 때 주로 가변 공간 요구에 초점을 맞추는 이유는, 입력의 크기가 증가함에 따라 가변 공간 요구가 기하급수적으로 증가할 수 있기 때문이다. 즉, 큰 입력에 대해 알고리즘이 얼마나 효율적으로 동작하는지를 파악하는 데 중요한 역할을 하기 때문이다.
반면 상수 공간 요구는 입력의 크기와 관계없이 일정하므로, 전체 메모리 사용량에 대한 영향은 상대적으로 작다. 따라서 일반적으로 알고리즘의 공간 복잡도를 분석할 때는 주로 가변 공간 요구에 대한 분석을 진행하게 된다.
2) 시간 복잡도(time complexity)
개요
- 프로그램에 의해 소요되는 시간은 컴파일 시간(compile time)과 실행(run 또는 execution) 시간 을 합한 것이다. 컴파일 시간은 인스턴스 특성에 의존하지 않기 때문에 고정 공간 요구와 유사하다.
- 또한 프로그램이 일단 정확히 수행되는 것이 검증되면, 그 프로그램을 다시 컴파일하지 않고도 여러 번 수행할 수 있다. 그렇기 때문에 프로그램의 실행 시간만 염두 해두면 된다.
- 특정 하드웨어나 소프트웨어를 고려하지 않는 알고리즘의 추상적인 실행시간이다.
- 알고리즘을 이루는 명령어들이 몇 번이나 실행되는지, 그 실행횟수에 의해 결정된다. 그리고 알고리즘 수행시 사용되는 기본 연산의 빈도수를 차수(degree)로 표현한 것이다.
특징
- 프로그램 분석의 표현은 명령문이 실제 수행되는 데 소요되는 시간과 수행되는 빈도수를 곱해서 나타낸다. 프로그램의 계산 차수가 여러 개의 항목으로 되어 있다면 그중 가장 높은 항을 택하여 계산 차수로 사용한다.
- 프로그램의 수행 시간은 알고리즘 구조, 프로그램에 대한 입력, 컴퓨터의 메모리 크기 및 사용자 수 등에 영향을 받기 때문에 정확한 산출은 어렵다. 그러므로 Ο, Ω, Θ와 같은 근사적 분석법을 이용하여 대략적인 차수로 복잡도를 나타낸다.
프로그램 단걔(Program Step)
- 프로그램 단계(Program Step)는 실행 시간이 인스턴스 특성에 구문적으로 또는 의미적으로 독립성을 갖는 프로그램의 단위이다.
- 단계 수를 구할 때, 테이블 방식(tabular method)을 이용할 수 있다. 이는 단계 수 테이블을 만들기 위해서는 먼저 명령문에 대한 단계 수를 결정해야 한다. 이를 'steps/execution' 줄여서 's/e'라 한다.
- 그리고 명령문이 수행되는 횟수, 즉, 빈도수(frequency)를 계산해야 한다. 비실행 명령문의 빈도수는 0이다. 이에 s/e를 곱하면, 각 명령문에 대한 총 단계 수(total steps)를 구할 수 있다. 이 총계를 전부 합하면 전체 함수의 단계 수가 된다.

프로그램 단계 명령문 실행 시간
- 유의할 점은 프로그램 세그먼트에 의해 표현되는 계산양은 다른 세그먼트에 의해 표현되는 계산 양과 다르다는 것이다. 즉, 프로그램의 서로 다른 부분들이 각각 다른 양의 계산을 수행한다는 것을 의미한다. 어떤 프로그램은 매우 많은 양의 계산을 수행하는 세그먼트를 가질 수 있고, 다른 프로그램은 간단한 계산만 수행하는 세그먼트를 가질 수 있다. 따라서, 프로그램의 전체 시간 복잡도를 계산할 때는 각 세그먼트에서 어떤 계산이 수행되고, 그 계산이 얼마나 많이 수행되는지를 고려해야 한다. 예를 들어, 알고리즘 내에 반복문이 있는 세그먼트와 그렇지 않은 세그먼트가 있다면, 반복문이 있는 세그먼트는 같은 코드라도 반복문이 실행되는 횟수에 따라 더 많은 계산을 수행하게 된다. 따라서 이 세그먼트의 계산양은 반복문이 없는 세그먼트와 비교하여 크게 증가하게 된다. 이런 차이들이 프로그램 전체의 시간 복잡도를 결정하는 데 중요한 역할을 한다.
- 유의할 점은 프로그램 세그먼트에 의해 표현되는 계산양은 다른 세그먼트에 의해 표현되는 계산 양과 다르다는 것이다. 즉, 어떤 프로그램은 매우 많은 양의 계산을 수행하는 세그먼트를 가질 수 있고, 다른 프로그램은 간단한 계산만 수행하는 세그먼트를 가질 수 있다. 따라서, 프로그램의 전체 시간 복잡도를 계산할 때는 각 세그먼트에서 어떤 계산이 수행되고, 그 계산이 얼마나 많이 수행되는지를 고려해야 한다.
예를 들어, 알고리즘 내에 반복문이 있는 세그먼트와 그렇지 않은 세그먼트가 있다면, 반복문이 있는 세그먼트는 같은 코드라도 반복문이 실행되는 횟수에 따라 더 많은 계산을 수행하게 된다. 따라서 이 세그먼트의 계산양은 반복문이 없는 세그먼트와 비교하여 크게 증가하게 된다. 이런 차이들이 프로그램 전체의 시간 복잡도를 결정하는 데 중요한 역할을 한다. - 예를 들어, a = 2와 같은 간단한 지정문을 한 단계로 간주할 수 있고, a = 2b + 3c/d - e + f/g/a/b/c 와 같이 좀 더 복잡한 연산문 역시 한 단계로 간주할 수도 있다. 이때 요구되는 점은, 한 단계로 간주되는 각 명령문을 실행하는데 필요한 시간이 인스턴스 특성에 독립적이어야 한다는 것이다.
알고리즘의 시간 복잡도(Time Complexity)는 알고리즘이 어떤 문제를 해결하는 데 얼마나 많은 시간이 걸리는지를 측정한 것이다. 이를 분석함으로써 알고리즘의 효율성을 평가하고, 다른 알고리즘과의 성능을 비교할 수 있다.
시간 복잡도는 일반적으로 입력 데이터의 크기에 따라 얼마나 많은 계산 단계가 필요한지를 나타낸다. 예를 들어, 배열에서 특정한 원소를 찾는 알고리즘의 경우, 최악의 시나리오는 배열의 모든 원소를 확인해야 하는 경우일 것이다. 이때, 입력 데이터의 크기(즉, 배열의 길이)가 n일 때, 알고리즘은 n단계가 필요하므로 이 알고리즘의 시간 복잡도는 O(n)이 된다.
이렇게 시간 복잡도를 나타낼 때는 보통 빅 오(Big O) 표기법을 사용한다. 빅 오 표기법은 알고리즘의 최악의 경우를 나타내며, n이 증가함에 따라 어떻게 성능이 변화하는지를 나타내는 방법이다.
예를 들어, O(1)은 입력 데이터의 크기와 상관없이 항상 일정한 시간이 걸리는 알고리즘을, O(n)은 입력 데이터의 크기에 비례하여 시간이 걸리는 알고리즘을, O(n^2)는 입력 데이터의 크기의 제곱에 비례하여 시간이 걸리는 알고리즘을 나타낸다.
다만, 빅 오 표기법은 최악의 경우의 시간 복잡도를 나타내기 때문에, 실제로 알고리즘이 동작하는데 걸리는 시간을 정확하게 반영하지는 않는다. 이는 알고리즘의 성능을 과대평가하거나 과소평가할 수 있음을 의미한다. 따라서 시간 복잡도는 알고리즘의 효율성을 대략적으로 추정하는 도구일 뿐, 성능을 정확하게 예측하는 척도는 아니다.
(3) 점근적 표기법(asymptotic notations)
알고리즘 수행시 연산의 빈도수를 결정하려는 것은 같은 기능을 수행하는 두 프로그램의 시간 복잡도를 비교하거나 인스턴스 특성의 변화에 따라 실행시간의 증가를 예측하기 위한 것이다.
예) 18n^3 + 34n^2 + 3n + 2 에서 수행 성능은 n^3항에 의해 좌우된다.
1) Big oh 함수(O)
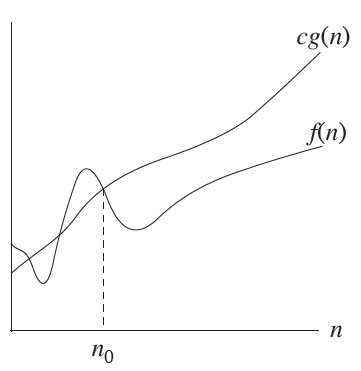
- big oh 함수 O는 어떤 식의 최고 차수의 상한을 나타내는 것이다.
- n ≥ n0 를 만족하는 모든 n에 대하여 f(n) ≤ cg(n)인 조건을 만족하는 두 양의 상수 c와 n0가 존재하기만 하면f(n) = O(g(n))에 사용된 기호 '='는 좌우가 '동등하다'의 의미가 아니라 '~이다' 라는 의미이다.
- 함수 f(x) = ax^2 + bx + c는 a, b, c의 값에 따라 상수식이 될 수도 있으니 이차식 이하이다. f(x)가 이차식 이하라는 것을 나타내기 위해서 f(x) = O(x^2)으로 표현한다. 즉, 어떠한 상황에서도 프로그램의 수행시간은 x^2의 상수배 이하가 된다.
- 알고리즘 시간 복잡도 O(1)은 알고리즘의 수행시간이 입력 데이터 수와 관계없이 일정하다는 것을 의미하낟.
- 일반적으로 메모리를 많이 사용하면 수행시간이 짧게 되고, 적게 사용하면 수행시간은 길어진다. 따라서 알고리즘 성능은 수행되는 데 필요한 시간과 공간에 대한 함수로 살펴볼 수 있다.
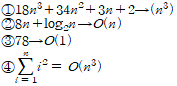
①은 O(x^4)도 가능하다.
2) Omega함수(Ω)
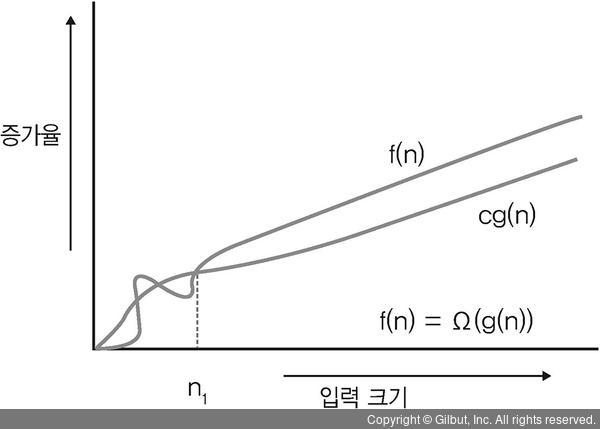
- Omega 함수 Ω는 O와 반대로 어떤 식의 최고 차수의 하한을 나타내는 것이다.
- n ≥ n0 를 만족하는 모든 n에 대하여 f(n) ≥ cg(n)인 조건을 만족하는 두 양수 상수 c와 n0가 존재하면 f(n) = O(g(n))이다.
- 함수를 Ω로 나타낼 때 최고차항의 차수 이외는 모두 무시할 수 있다는 것은 O와 마찬가지이다. 최고차수의 상한이 아닌 하한이라는 점이 다르다.
1.함수 f(x) = 18x^2 + 15x + 25이라는 수식에서 f(x) = Ω(x), f(x) = Ω(x^2)는 모두 다 성립하지만, f(x) = Ω(x^3), f(x) = Ω(x^4)등은 성립하지 않음을 의미한다.
2.f(n)=2n+1이면, n>1에 대하여 2n+1>n이므로, f(n) = Ω(n) 이다.
3.Omega함수(Ω)에서의 하한 설정은 어떤 알고리즘을 수행하기 위한 최소 시간을 의미한다.
3) Theta함수(θ)
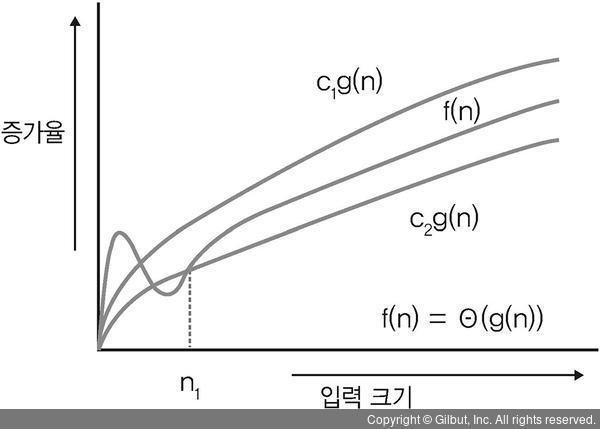
- Theta함수 θ는 빅오 함수와 오메가 함수를 합쳐놓은 것이다.
- n ≥ n0 를 만족하는 모든 n에 대하여 c1g(n) ≤ f(n) ≤ c2g(n)인 조건을 만족하는 세 양의 상수 c1, c2와 n0가 존재하기만 하면 f(n) = θ(g(n))이다.
- 어떤 함수에서 최고차수의 상한과 최고차수의 하한을 동시에 지정함으로써 함수의 정확한 최고 차수를 나타낼 수 있다.
- 임의의 두 함수 f(n)과 g(n)에 대한 f(n) = θ(g(n))이면 f(n) = O(g(n)), f(n) = Ω(g(n))이고 그 역도 성립한다.
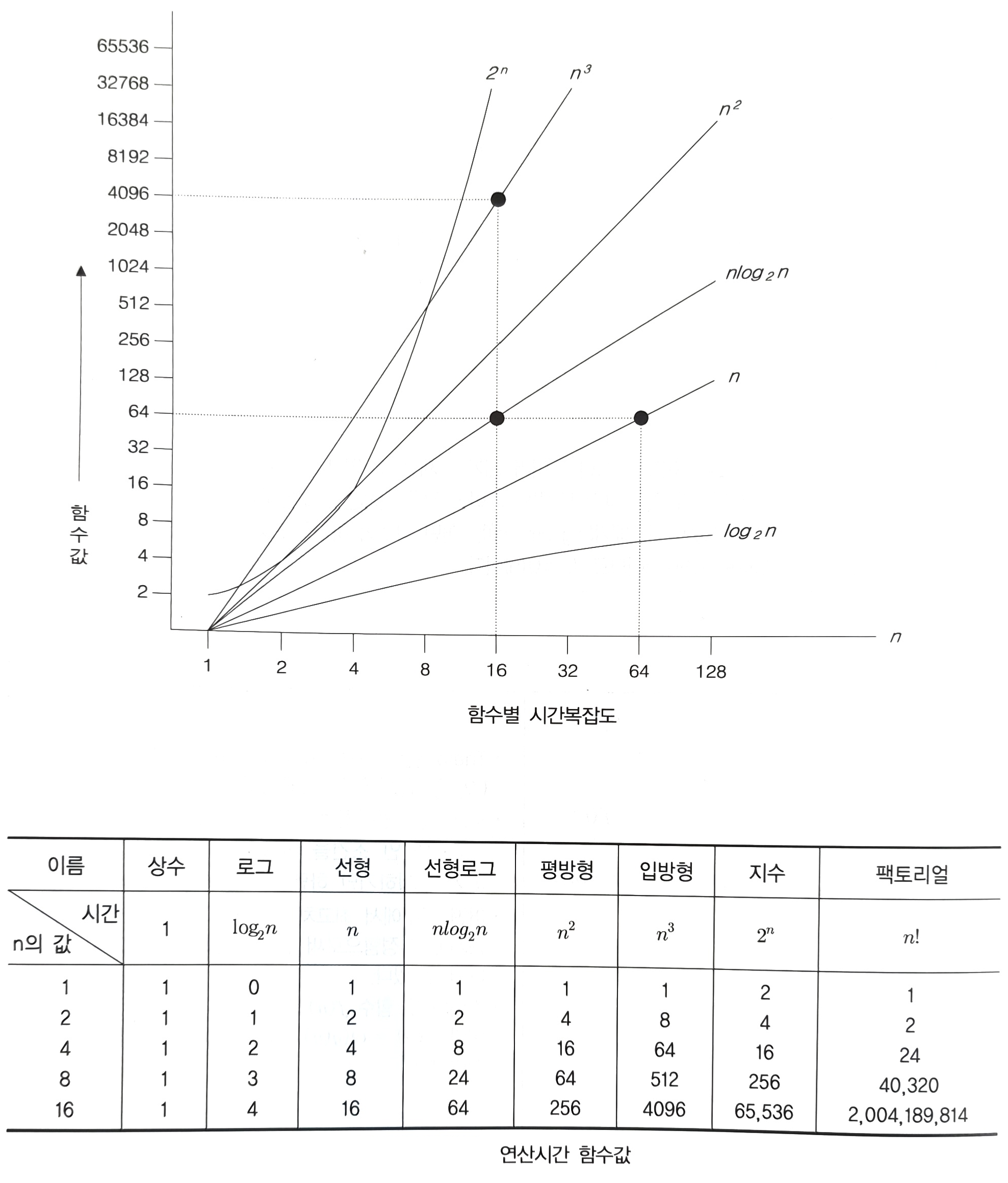
- 위 그림과 표에서 볼 수 있듯이 n이 증가항에 따라 로그보다 지수일때 더욱 빠르게 증가하는 것을 안 수 있다. 어떤 알고리즘의 연산시간은 n이 충분히 클 때, 아래와 같은 관계를 가진다.
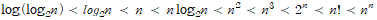

빅-오 함수로 시간 복잡도를 표시하는 이유는 몇 가지가 있다.
1. 추상화: 시간 복잡도를 빅-오 표기법으로 나타내면, 세부적인 구현 세부 사항이나 하드웨어, 프로그래밍 언어 등에 의존하지 않고 알고리즘의 효율성을 쉽게 비교하고 이해할 수 있다. 따라서 빅-오 표기법은 알고리즘의 상대적인 성능을 측정하는 데 매우 유용한 도구다.
2. 최악의 경우 분석: 빅-오 표기법은 알고리즘의 최악의 경우 성능을 설명한다. 이를 통해 프로그래머는 알고리즘이 데이터가 매우 클 때나 조건이 최악일 때 얼마나 잘 동작하는지를 평가할 수 있다.
3. 입력 크기에 대한 성능 분석: 빅-오 표기법은 입력 데이터의 크기에 따른 알고리즘의 성능을 예측하는데 사용된다. 이것은 주어진 문제를 해결하는 데 얼마나 많은 시간이나 공간이 필요할지 예상하는 데 중요하다.
4. 스케일링: 대규모 데이터 세트에서의 알고리즘 성능을 이해하는 데 특히 유용하다. 예를 들어, 데이터 크기가 두 배로 증가했을 때 알고리즘의 실행 시간이 어떻게 변하는지를 예측할 수 있다.
3.알고리즘 설계 기법
(1) 분할 정복(divide and conquer)기법
1) 순환적 프로그램의 3단계
- 분할 단계: 현재의 문제를 같은 문제를 다루는 다수의 부분 문제로 분할한다.
- 정복 단계: 부분 문제를 재귀적으로 풀어서 정복한다. 부분 문제의 크기가 충분히 작으면 직접적인 방법으로 푼다.
- 결합(연합)단계: 부분 문제의 해를 결합하여 원래 문제의 해가 되도록 만든다.
2) 사례
- 분할 단계와 정복 단계만 수행하는 예: 퀵 정렬, 이진검색, 순환프로그램, Hanoi(하노이) 등
- 모든 단계(연합단계까지 포함)를 수행하는 예: 2-way-merge 정렬
(2) 동적 계획(dynamic programming) 기법
1) 정의
- Bottom Up접근방식으로, 작은 단계의 문제를 해결하고, 그 답을 저장한 후 계속 그것을 이용하여 더 큰 문제를 해결해 나간다.
2) 사례
- 방향 그래프에서 모든 쌍의 최단 경로를 찾는 알고리즘(Dijkstra 알고리즘, Bellman and Ford알고리즘)
- 방향 그래프에서 이행적 폐쇄를 구하기 위한 알고리즘(A*, A+)
(3) 탐욕(greedy) 기법(희망적인 전략기법)
1) 정의
- 최적의 해를 구하기 위해 선택할 당시 가장 최고인 것처럼 보이는 선택을 하지만, 지역적으로 최적이 항상 전체적으로 최적일 수 없기에 알고리즘이 최종적으로 최적의 해를 주는지 확인해야 한다.
2) 사례
- 무방향 그래프에서 최소 비용 신장트리를 찾기 위한 알고리즘으로 Kruskal의 알고리즘과 Prim의 알고리즘이 있다.
- 방향 그래프에서는 단일 출발점에서 최단 경로를 찾기 위한 Dijkstra의 알고리즘을 이용한다.
(4) 되추적(backtracking)기법
1) 정의
- 어떤 노드에서 해당이 나올 가능성을 점검한 후, 해답이 나올 가능성이 업삳고 판단되면 그 노드의 이전 노드로 되돌아가서("backtracking") 다른 노드로부터 해답을 다시 찾으려는 기법
2) 사례
- 트리(tree), 그래프(graph)의 운행(traversal)
순환적 프로그램
1. 순환적 프로그램(Recursive Program)의 개념
(1) 기본 개념
1) 정의
- 순환(recursion, 재귀)이란 어떤 알고리즘이나 함수가 자기 자신을 호출하여 문제를 해결하는 프로그램 기법이다. 프로그램에서 한 procedure가 어떤 procedure를 반복적으로 호출하는 경우 문제 자체에 내재된 순환적인 특성을 이용한다.
- 문제를 형태가 유사한 여러 개의 작은 문제들로 나누고 각각 동일한 해결기법을 계속적으로 적용한 다음 그 결과들을 연합하여 문제를 해결하는 기법이다.
- 문제를 해결하기 위해서 분할 및 정복(divide-and-conquer)방식을 따른다.
2) 특징
- 문제해결에서 반복문 이용 분야와 순환문 이용 분야를 구별하지는 않는다.
- 순환함수는 단계를 진행함에 따라 종료 조건에 접근해 가야하며, 입력 값이 완료 조건에 만족할 때 자신을 호출하지 않고 출력 값을 계산한다.
- 재귀적 접근 방법은 하나의 문제를 여러 개의 작은 문제들로 나누는 방법이다. 이때 작은 문제는 모두 같은(Type)이어야 한다는 제약이 있다.
- 재귀적 접근 방법의 또 다른 특성으로 종료조건(Terminate Condition)을 들 수 있다.
→ 순환 알고리즘은 자기 자신을 순환적으로 호출하는 부분과 순환 호출을 멈추는 부분으로 구성되어 있다. 만약 순환 호출을 멈추는 부분이 없다면, 시스템 스택을 다 사용할때까지 순환적으로 호출되다가 결국 오류를 내면서 멈출 것이다.
mystery(n)
{
if(n <= 1)
mystery(n) = 1
else
mystery(n) = mystery(n-1) + mystery(n-2)
}- 위 예제에서 mystery(4)을 계산하기 위하여 순환 기법을 사용하면 다음과 같다.
mystery(4) = mystery(3) + mystery(2)
= mystery(2) + mystery(1) + mystery(2)
= mystery(1) + mystery(0) + 1 + mystery(2)
= 1 + 1 + 1 + mystery(1) + mystery(0)
= 1 + 1 + 1 + 1 + 1
= 5
3) 장점
- 프로그램을 읽기가 쉽고 정확성을 증명하기가 쉽다.
- 문제자체가 순환적으로 정의되어 있는 경우, 순환적 프로그램의 작성이 간단해진다.
- 이진트리 2개의 동일성 비교(equality testing)는 순환적 프로그램으로 작성하기에 아주 적절하다.
4) 단점
- 순환 함수는 반복 함수보다 실제로 단계 수가 더 작다. 통상적으로 순환 함수가 작은 단계 수를 가지더라도 반복 함수보다 실행속도는 더 느리다.
- 왜냐하면 순환 함수의 단계가 반복 함수의 단계보다 활성화 레코드 생성, 필요한 정보 설정 등 실행환경을 만드는 데 시간이 평균적으로 더 많은 시간이 걸리기 때문이다.
- 모든 지역 변수와 인수, 복귀 주소 등을 할당할 수 있는 스택 공간이 있어야 한다.
- 순환적 프로그램을 사용하면, 스택이 필요하므로 알고리즘의 공간 복잡도(space complexity)는 보통 더 증가한다.
재귀호출의 내부적 구현
프로그래밍 언어에서 하나의 함수가 자기 자신을 다시 호출하는 것은 다른 함수를 호출하는 것과 동일하다. 즉 복귀주소가 시스템 스택에 저장되고 호출되는 함수를 위한 매개변수(parameter)와 지역 변수를 스택으로부터 할당받는다. C, PASCAL, C++, Java등의 현대적인 프로그래밍 언어에서 순환을 지원하지만 FORTRAN, COBOL과 같은 고전적인 언어에서는 지역변수가 없거나 있더라도 정적으로 할당되므로 순환이 불가능하다. 즉, 함수호출마다 새로운 지역변수를 만들지 못하면 이전 호출과 구분할 수가 없어서 순환 호출이 불가능하다.
(2) 순환적 프로그램의 고려사항
- 순환 호출을 끝낼 수 없다면 순환 방법을 사용하지 말 것
- 프로그램의 특성이 순환구조에 의해 간단해 질 경우 순환 방법이 적합하다.
- 한 procedure가 어떤 procedure를 반복적으로 호출하는 경우 순환방법을 적용한다.
- 프로그램을 단순화시키고자 할 때 사용한다.
- 복귀를 위한 정보의 저장과 탐색에 별도의 스택 기억공간이 필요하며, 호출한 프로그램을 수행하기 위한 많은 시간이 소요된다.
- 순환의 깊이가 너무 깊으면 활성화레코드의 생성으로 인해 할당할 메모리가 부족하여 프로그램 실행이 중단되는 문제도 발생할 수 있다.
(3) 순환적 알고리즘을 반복구조로 변환
- 순환적 알고리즘에는 반드시 초기조건이 명시되어 있다 (순환함수의 경계조건으로부터 반복구조의 초기조건을 구할수 있다.)
- 순환적 알고리즘의 현재 값과 다음 값의 관계로부터 다음 값을 구하는 관계식을 얻는다.
- 위에서 얻은 관계식을 반복 구조 문장으로 나타낸다.

순환의 종류
1. 직접 순환(direct recursion):함수가 직접 자신을 호출
2. 간접 순환(indirect recursion): 다른 제 3의 함수를 호출하고, 그 함수가 다시 자기 자신을 호출
(4) 순환적 프로그램의 종류
1) 팩토리얼(Factorial) 계산
- 정수 n에 대한 n! 계싼은 순환적 알고리즘에 의해 계산될 수 있다
- 팩토리얼 계산식: factorial(n) = n * factorial(n-1)
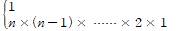
2) 피보나치 수열
- 피보나치 수열은 첫 번째 항과 두 번째 항에 대해서는 각각 값이 0,1이지만, 세 번 째항 이상에 대해서는 이전 두 항을 더한 값으로 정의되는 수열이다.
2 피보나치 수열
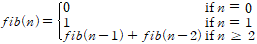
3) 하노이 탑
- 재귀호출을 통하여 문제를 쉽게 해결할 수 있는 가장 대표적인 예 중 하나로 '하노이의 탑(The Tower of Hanoi)'문제가 있다. 하노이의 탑 문제는 원판을 옮기는 문제이다. 원판들을 옮길 때, 다음과 같은 제약사항이 있다.
- 한번에 하나의 원판만 이동할 수 있다.
- 맨 위에 있는 원판만 이동할 수 있다. → 중간에 있는 원판을 억지로 뺴낼 수 없다는 의미
- 크기가 작은 원판 위에 큰 원판이 있을 수 없다 → 크기가 큰 원판 위에만 작은 원판을 놓을 수 있다.
- 중간 막대를 이용할 수 있으나, 앞의 조건 3가지를 만족해야 한다.

- 하노이 탑 알고리즘
#include <stdio.h>
void hanoi_tower(int n, char from, char tmp, char to)
{
if (n==1) printf("원판1을%c에서 %c로 옮긴다. \n", from, to);
else{
hanoi_tower(n-1, from, to, tmp);
printf("원판 %d을 %c에서 %c로 옮긴다. \n", n, from, to);
hanoi_tower(n-1, tmp, from, to); }}
void main()
{
hanoi_tower(n, 'A', 'B', 'C'): /*n개를 옮기는 경우 */2. The Master Theorem

레코드(record)
(1) 정의
- 레코드는 데이터 구성의 논리적인 단위로서 프로그램 실행 시 처리 단위가 된다.
- 서로 관계있는 여러 필드들을 한 개의 조로 묶어서 구성한 데이터 구조이다.
- 배열(array)과 레코드(record)는 여러 항목들의 데이터를 하나의 그룹 단위로 나타내는 자료구조이다.
- 레코드를 구성하는 하나의 항목을 멤버(member)또는 필드(field)라고 하며, 레코드들이 모여서 하나의 파일(file)을 구성한다.
- C언어에서는 struct라는 자료구조가, Pascal에서는 record라는 자료구조가 레코드의 기능을 제공한다.
- 배열은 데이터 원소의 크기와 데이터형이 동일한 반면, 레코드는 데이터 원소의 크기와 데이터형이 다르다.
- 레코드를 구성하는 필드는 그 필드의 이름에 의해 호출ㆍ참조된다.
되지만, 배열을 구성하는 원소는 그 원소가 저장된 위치를 가리키는 배열의 인덱스(index)에 의해 호출 ㆍ참조된다.
즉, 레코드(record)는 컴퓨터 과학에서 사용하는 기본적인 데이터 구조 중 하나로, 관련 정보의 집합을 의미한다. 레코드는 일반적으로 다른 데이터 타입의 여러 필드로 구성되며, 각 필드는 서로 다른 값을 가질 수 있다.
예를 들어, 학생 데이터베이스에서 각 학생은 별도의 레코드로 표현될 수 있고, 이 레코드는 '이름', '학번', '학년', '전공' 등의 필드를 포함할 수 있다.
student_record = {
"name": "John Doe",
"student_id": 123456,
"grade": "Sophomore",
"major": "Computer Science"
}위의 Python 예제에서 student_record는 하나의 레코드를 나타내며, 이는 여러 개의 필드로 구성된 딕셔너리이다.
레코드는 데이터베이스에서 행(row) 또는 튜플(tuple)이라고도 불리며, 프로그래밍 언어에 따라 구조체(struct), 클래스(class) 등으로도 표현된다.
레코드를 사용하면 관련 있는 정보를 하나의 단위로 그룹화하여 처리할 수 있으므로 데이터 관리가 쉬워진다. 또한 필드를 추가하거나 삭제하는 등의 구조적 변경이 수월하기 때문에 데이터의 유연성이 높아진다.
(2) 레코드의 표현
1) 고정 길이 레코드
- 레코드 삭제 시의 어려움: 고정 길이 레코드에서 특정 레코드를 삭제하면 그 자리는 공백이 되어버리고, 이 공백을 다른 레코드로 채우려면 추가적인 조작이 필요하다. 이런 비효율적인 공간 활용은 공간 낭비를 가져올 수 있다.
- 부가적인 블록 액세스 필요성: 고정 길이 레코드의 블록 크기가 데이터베이스 블록의 크기와 딱 맞지 않을 경우, 추가적인 블록 액세스가 필요할 수 있다. 예를 들어, 레코드가 블록 경계를 넘어가는 경우, 해당 레코드에 접근하기 위해 두 블록을 모두 액세스해야 할 수 있다.
2) 가변 길이 레코드가 필요한 경우
- 한 파일 내에 여러 유형의 레코드 저장: 파일 내에 다양한 유형의 레코드를 저장해야 할 경우, 각 레코드 유형의 크기가 다를 수 있다. 이런 경우 가변 길이 레코드를 사용하면 공간을 효율적으로 활용할 수 있다.
- 한 파일 내에 가변 필드를 허용하는 레코드 저장: 레코드의 일부 필드의 크기가 변할 수 있을 때(예를 들어, 문자열 길이가 다른 경우), 가변 길이 레코드를 사용하면 공간을 더 효율적으로 활용할 수 있다.
- 반복 필드 허용: 레코드 내에 일련의 값(반복 필드)이 포함될 수 있으며, 이 값의 수가 레코드마다 다를 경우, 가변 길이 레코드를 사용하면 효율적으로 데이터를 저장할 수 있다.
(3) 레코드의 구성
1) 논리적 레코드(logical record)
논리적 레코드는 사용자나 응용 프로그램이 보는 데이터베이스의 레코드를 의미한다. 이는 종종 데이터베이스를 이루는 테이블의 한 행으로 이해할 수 있다. (즉, 프로그램에서 처리되는 기본 단위로 하나의 블록을 구성하는 각 레코드) 예를 들어, 은행의 고객 데이터베이스에서 논리적 레코드는 개별 고객에 대한 모든 정보(이름, 주소, 계좌번호 등)를 포함할 수 있다.
2) 물리적 레코드(Physical Record) = 블록(block)
물리적 레코드는 데이터베이스가 실제 디스크나 다른 저장 매체에 데이터를 저장하는 방식을 의미한다. 물리적 레코드의 구조와 크기는 종종 데이터베이스 관리 시스템(DBMS) 또는 파일 시스템에 의해 결정되며, 종종 데이터를 블록 또는 페이지로 조직화하는 데 사용된다. 물리적 레코드는 하나의 논리적 레코드를 포함하거나, 여러 논리적 레코드를 포함하거나, 하나의 논리적 레코드가 여러 물리적 레코드에 걸쳐 있을 수 있다.
- 물리적 레코드는 저장 매체에 기록되는 데이터의 단위로, 디스크나 테이프 등의 보조 기억장치와 주 기억장치 간의 입출력 처리 단위이다. 이는 일반적으로 "블록"이라고도 불린다. 하나의 물리적 레코드는 하나 이상의 논리적 레코드를 포함할 수 있다.
- 하나의 물리적 레코드 또는 블록이 여러 개의 논리적 레코드를 담을 수 있고, 반대로 하나의 논리적 레코드가 여러 물리적 레코드에 분산될 수도 있다.
- 파일에서 데이터를 읽거나 쓸 때는 여러 논리적 레코드를 그룹화하여 블록 단위로 한 번에 처리하는 것이 일반적이다. 이는 입출력 연산의 효율성을 높이는 데 도움이 된다.

- IRG(Inter Record Gab): 레코드와 레코드 사이의 공간
- IBG(Inter Block Gab): 블록과 블록 사이의 공간
- 블록킹(blocking): 몇 개의 논리적 레코드를 하나의 물리적 레코드(블록)로 구성하는 작업으로, 하나의 블록을 구성하는 논리 레코드의 수를 블록킹 인수(blocking factor)라 한다.
