순서 리스트(Ordered List)

(1) 정의

• 순서리스트는 선형리스트라고도 하는데, 선형 리스트(linear list)란 어떤 순서에 의해 나열된 항목들이 유한 개 있는 데이터들의 모임으로서, 컴퓨터에서 많이 사용되는 자료구조이다. (일반적으로 값의 크기에 따라 정렬된 상태로 유지된다.)
• 리스트를 구성하는 원소 상호간에 1:1의 관계를 가지면서 명확한 선후 관계로 구성되는 자료구조이다.
• 리스트를 기억공간에 저장하는 방법으로는 각 원소들을 메모리상에 연속적(배열) 또는 불연속적(연결리스트)으로 위치한다.
• 순서리스트(ordered list)란 삽입과 삭제를 할 수 있는 순서적 자료의 집합이다. 다만, 삽입과 삭제를 하더라도, 항상 리스트가 정렬된 상태로 유지되어야 한다. 따라서 추가적인 처리가 필요하다.
• 순서리스트는 검색 작업에 효율적이다. 리스트가 정렬되어 있기 때문에 이진 탐색(binary search)같은 효율적인 검색 알고리즘을 사용할 수 있다. 이는 순서가 없는 리스트에 비해 훨씬 빠른 검색 속도를 제공한다.
• 순서리스트(ordered list)는 배열구조(연접구조)와 연결리스트가 있다.

선형 리스트(Linear List) (연접 리스트(Dense List))

(1) 정의

1. 선형 리스트가 연속적인 기억공간의 1차원 배열을 이용하여 표현되었을 때 순차리스트(sequential list)라고 한다.
2. 기억장소에 자료를 물리적으로 인접하면서 연속적으로 저장시키는 리스트로, 배열구조이다.
3. 임의의 원소에 접근할 때 포인터 없이 색인번호(index number)를 사용하여 리스트의 시작 주소로부터 원소들의 상대적인 위치를 계산할 수 있다.
4. 임의접근(random access)이 가능하여 직접파일에서 이용된다.

(2) 장점

1. 임의의 위치에 있는 원소 값을 아주 쉽게 얻을 수 있다. 즉, 검색이 용이하다.
2. 리스트구조에서 i번째 원소의 값을 수정하는 연산이 많이 일어날 경우 이 리스트를 연결리스트로 구현하는 것보다 배열로 구현하는 것이 더 좋다.
3. 고정된 수의 자료를 지정할 경우 기억공간 이용이 효율적이다

(3) 단점

1. 원소 삼입과 삭제 시 이동(repacking)시간이 많이 필요하다.
2. 컴파일러가 기억장소를 정적(Static)배당하므로 기억장소 사용 효율성이 떨어진다.
3. 물리적으로 연속된 기억공간을 필요로 하므로, 외부 단편화(fragmentation)가 발생하다.

• repacking algorithm : 저장 공간 재분배의 간단한 방법으로 스택에서 과잉상태를 해결하는 방법이다.

(4) 연접리스트에서 원소의 삽입ㆍ삭제

1) 삼입(insertion)

예) 연접리스트에서 원소 삽입을 위한 평균이동횟수(Mi)를 구하기 위한 과정

1. 리스트의 인덱스1에 원소를 삽입할 경우 (n-1)+1회 이동한다
2. 리스트의 인덱스2에 원소를 삽입할 경우 (n-2)+1회 이동한다.
3. 리스트의 인덱스i에 원소를 삽입할 경우 (n-i)+1회 이동한다.
4. 리스트의 인덱스n에 원소를 삽입할 경우 (n-n)+1회 이동한다.

• n개 원소로 구성된 연접리스트에서 임의 원소 i가 어떤 위치에 삽입될 확률은 1/n이며, 임의의 위치에 원소를 삽입하기 위한 이동횟수의 총합은 다음과 같다.

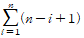
• 연접리스트에서 원소 삽입을 위한 평균 이동횟수 Mi는 다음과 같다.

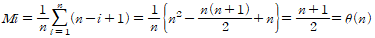
• 그러므로 길이가 n인 연결리스트에서 임의 원소를 삽입 시키기 위한 이동횟수가 원소 삽입을 위한 평균이동횟수가 된다.

2) 삭제(deletion)

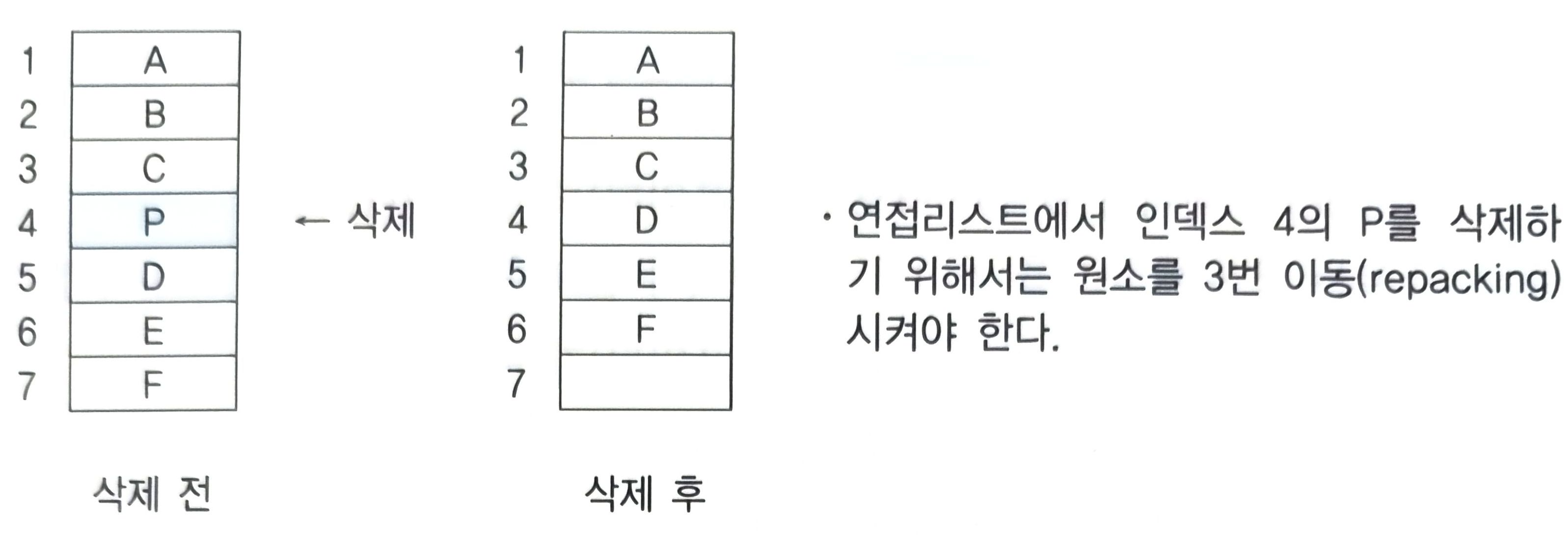
예) 연접리스트에서 원소 삭제를 위한 평균이동횟수(Md)를 구하기 위한 과정

1. 리스트에서 인덱스 1의 원소를 삭제할 경우(n-1)회 이동한다.
2. 리스트에서 인덱스 2의 원소를 삭제할 경우(n-2)회 이동한다.
3. 리스트에서 인덱스 i의 원소를 삭제할 경우(n-i)회 이동한다.
4. 리스트에서 인덱스 n의 원소를 삭제할 경우(n-n)회 이동한다.

• n개 원소로 구성된 연접리스트에서 임의의 원소 하나가 삭제될 확률은 1/n이며, 모든 원소를 삭제하기 위한 이동횟수의 총합은 다음과 같다.

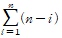
• 연접리스트에서 삭제를 위한 평균이동횟수 Md는 다음과 같다.

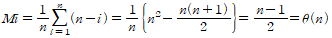
• 그러므로 길이가 n인 연접리스트에서 임의의 원소를 삭제하기 위한 이동횟수가 원소 삭제를 위한 평균이동횟수가 된다.

연결리스트(Linked List)

(1) 정의

1. 연접리스트의 문제점인 삽입과 삭제가 쉽도로 고안된 자료구조로, 삽입과 삭제가 빈번한 작업에 적합하다.
2. 연결리스트는 노드(Node)를 크게 데이터 필드와 링크 필드로 나누어 다음 노드가 기억된 공간의 주소를 이전 노드의 링크 필드에 기억시키는 방식으로 모든 노드들을 하나의 리스트로 연결한다.
3. 연결리스트는 논리적 데이터 순서와 물리적 데이터 순서가 동일하지 않으므로 후속 데이터 엑세스를 위해서는 포인터가 필요하다.
4. 노드들은 논리적으로는 순차적으로, 물리적으로는 비순차적으로 저장한다.

(2) 구조

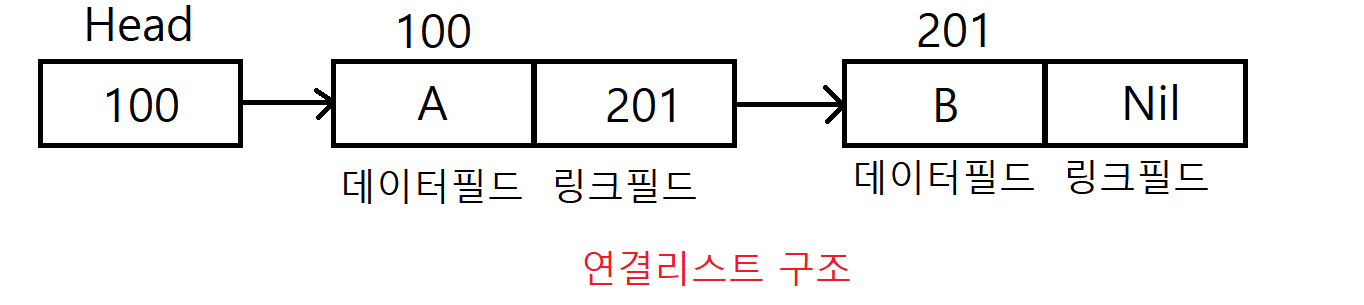
• 각 노드(node)는 데이터 필드와 링크 필드(포인터)로 구성된다.
• 데이터(Data): 정보를 저장하는 노드의 부분이다.
• 포인트(Pointer): 다음 노드의 위치를 가리키는 노드의 부분이다.
• 헤드(head): 연결 리스트는 첫 번째 노드를 가리키는 포인터다. 전체 리스트를 통제하는데 사용된다.
• 테일(Tail): 연결 리스트의 마지막 노드이다. 일반적으로 마지막 노드의 포인터는 null값(또는 nil)을 가리키며, 이는 더 이상 다음 노드가 없음을 의미한다.
• 링크 필드에는, 다음 노드가 기억된 주소(포인터)가 수록된다.
• 각 노드는 기억장소에서 서로 이웃해 있지 않아도 된다.

(3) 특징

• 연결리스트는 선형리스트의 노드 배열이 기억장치의 번지와 일치하지 않으며, 기억공간에 독립적으로 이루어진 리스트이다.
• 각 노드를 유용한 저장 공간 위치에 상관없이 저장시키고, 각 노드 사이의 관련성을 노드에 보관하여 1차원 배열관계를 유지하도록 함으로써 중간 노드의 삽입과 삭제를 용이하게 하는 리스트이다.
• 자료의 배열이 기억장소의 주소와 일치하지 않으며, 기억공간이 독립적이다. 즉, 물리적으로 연속성이 없다.
• 각 노드는 기억 장소에서 서로 이웃해 있지 않아도 되므로, 기억공간을 효율적으로 활용할 수 있다.
• 새로운 노드가 필요하면 기억장소를 동적 할당한다.

(4) 연결리스트의 장점

• 동적 크기: 연결 리스트는 실행중에 크기르 변경할 수 있다. 이는 배열과는 대조적으로, 배열은 고정된 크기를 갖는다.
• 노드를 연속적으로 저장하지 않아도 된다. 즉, 각 노드는 메모리의 유용공간의 위치에 관계 없이 저장이 가능하다.
• 노드의 삽입ㆍ삭제가 쉽다. 즉, 리스트의 연결(combine)과 분리(split)가 용이하다.
• 정적인 파일보다는 다양하고 변화 있는 파일에서 효과적으로 사용된다.
• 외부단편화(fragmentation)가 발생하지 않아 전체 기억공간의 사용 효율성이 좋다.
• 여러 개의 리스트를 한 개의 리스트로 쉽게 만들 수 있다. (합병이 용이)

(5) 연결리스트의 단점

• 추가 메모리 오버헤드: 포인터의 저장을 위한 기억장소가 요구되므로 기록밀도가 배열구조보다 낮다.
• 임의의 원소의 값을 수정하는 연산이 일어날 경우 많은 탐색시간을 필요로 한다.
• 무작위 접근이 비효율적: 임의의 문자를 접근하기 위해서는 처음부터 순차 탐색을 해야만 한다. 즉, 배열과 달리 무작위 접근이 비효율적이다.
• 알고리즘 구현이 복잡하다.