알고리즘 연습 방법

• 알고리즘을 잘 작성하기 위해서는 잘 작성된 알고리즘을 이해하고, 스스로 만들어봐야 함
  • 모사! 그림을 잘 그리기 위해서는 잘 그린 그림을 모방하는 것부터 시작

이번 챕터부터 알고리즘 시작이다!

1. 연습장과 펜을 준비
2. 알고리즘 문제를 읽고 분석
3. 간단하게 테스트용으로 매우 간단한 경우부터 복잡한 경우 순서대로 생각해보면서, 연습장과 펜을 이용하여 알고리즘을 생각해본다.
4. 가능한 알고리즘이 보이면, 구현할 알고리즘을 세부 항목으로 나누고, 문장으로 세부 항목을 나누어 적어본다.
5. 코드화하기 위해, 데이터 구조 또는 사용할 변수를 정리하고
6. 각 문장을 코드 레벨로 적는다.
7. 데이터 구조 또는 사용할 변수가 코드에 따라 어떻게 변하는지 손으로 적으면서, 임의 데이터로 코드가 정상 동작하는지를 연습장과 펜으로 검증한다.

정렬 (sorting) 이란?

• 정렬 (sorting): 데이터를 특정한 기준에 따라 순서대로 나열하는 알고리즘이다.
• 정렬은 프로그램 작성시 빈번하게 필요로 함
• 다양한 정렬 알고리즘이 존재하며, 각기 다른 상황에 적합하고 서로 다른 시간 복잡도와 공간 복잡도를 가진다.

다양한 정렬 알고리즘 이해를 통해, 동일한 문제에 대해 다양한 알고리즘이 고안될 수 있음을 이해하고,
각 알고리즘간 성능 비교를 통해, 알고리즘 성능 분석에 대해서도 이해할 수 있음

1. 버블 정렬 (Bubble Sort): 인접한 두 요소를 검사하여 정렬하는 방법이다. 가장 간단하지만, 가장 비효율적인 정렬 알고리즘 중 하나로 시간 복잡도는 $O(n^2)$이다.
2. 선택 정렬 (Selection Sort): 가장 작은(또는 가장 큰) 요소를 선택하여 앞으로 이동시키는 방식으로 정렬하는 알고리즘입니다. 버블 정렬과 마찬가지로 비효율적인 방식으로, 시간 복잡도는 $O(n^2)$이다.
3. 삽입 정렬 (Insertion Sort): 각 요소를 적절한 위치에 삽입하는 방식으로 정렬하는 알고리즘이다. 데이터가 거의 정렬되어 있는 경우에는 매우 효율적일 수 있지만, 일반적으로는 $O(n^2)$의 시간 복잡도를 가진다.
4. 퀵 정렬 (Quick Sort): 분할 정복 방법을 사용하여 리스트를 정렬하는 효율적인 알고리즘이다. 피벗을 기준으로 작은 요소와 큰 요소를 나눈 후 재귀적으로 정렬한다. 평균 시간 복잡도는 $O(n log n)$이지만, 최악의 경우 $O(n^2)$가 될 수 있다.
5. 병합 정렬 (Merge Sort): 리스트를 절반으로 나누어 정렬하지 않은 리스트를 만든 후, 다시 병합하면서 정렬하는 방법입니다. 병합 정렬은 항상 $O(n log n)$의 시간 복잡도를 가진다.
6. 힙 정렬 (Heap Sort): 이진 힙 자료구조를 사용하여 정렬하는 알고리즘이다. 힙을 구성한 후, 가장 큰(또는 가장 작은) 요소를 제거하고 재구성하는 과정을 반복하여 정렬합니다. 시간 복잡도는 $O(n log n)$이다.

각 정렬 알고리즘은 그 특성에 따라 사용되는 곳이 다르며, 어떤 데이터에 대해 가장 효율적인지는 알고리즘의 특성과 데이터의 상태에 따라 다르다.

버블 정렬 (bubble sort) 란?

두 인접한 데이터를 비교해서, 앞에 있는 데이터가 뒤에 있는 데이터보다 크면, 자리를 바꾸는 정렬 알고리즘

버블 정렬(Bubble Sort)은 가장 간단하면서도 가장 기본적인 정렬 알고리즘 중 하나이다. 이름에서 알 수 있듯이, 이 알고리즘은 정렬되지 않은 각 요소를 "버블"처럼 목록의 상단으로 이동시키는 방식으로 작동한다.

버블 정렬의 작동 원리는 다음과 같습다.

1. 리스트의 처음부터 시작하여 인접한 두 개의 요소를 비교한다.
2. 이 두 요소가 올바른 순서(오름차순 또는 내림차순)로 정렬되어 있지 않으면 위치를 바꾼다.
3. 리스트의 끝에 도달할 때까지 이 과정을 계속 반복한다.
4. 만약 한 회전을 돌았는데도 위치를 바꾼 요소가 없다면, 그 때는 이미 모든 요소가 정렬된 상태이므로 정렬을 멈춘다.

예를 들어 [5, 3, 8, 4, 2]라는 배열을 오름차순으로 버블 정렬하면 다음과 같이 동작한다.

1. [3, 5, 8, 4, 2] - 5와 3의 위치를 바꿈
2. [3, 5, 4, 8, 2] - 8과 4의 위치를 바꿈
3. [3, 5, 4, 2, 8] - 8과 2의 위치를 바꿈
4. [3, 4, 5, 2, 8] - 5와 4의 위치를 바꿈
5. [3, 4, 2, 5, 8] - 5와 2의 위치를 바꿈
6. [3, 2, 4, 5, 8] - 4와 2의 위치를 바꿈
7. [2, 3, 4, 5, 8] - 3과 2의 위치를 바꿈

이제 모든 요소가 오름차순으로 정렬되었다.

버블 정렬은 간단하고 코드를 구현하기 쉽지만, 시간 복잡도는 O(n^2)로 비효율적이다. 이는 리스트의 모든 요소를 한 번 비교할 때마다 리스트를 한 번씩 다시 스캔해야 하기 때문이다. 그래서 데이터의 양이 많아질수록 처리 시간이 급격히 증가한다. 따라서 작은 데이터셋에 대한 정렐이나 알고리즘 학습에 주로 사용된다.

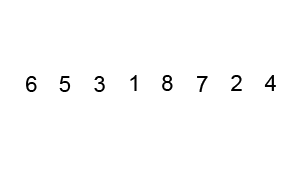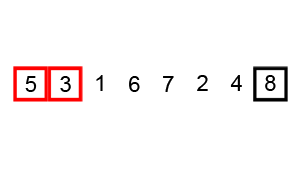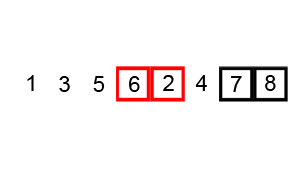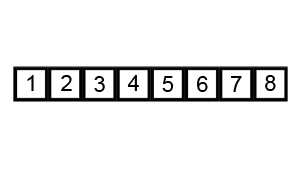
어떻게 코드로 만들까?

알고리즘 연습 방법에 기반해서 단계별로 생각해봅니다.

1. 데이터가 두 개일 때, 버블 정렬 알고리즘 방식으로 정렬해 보자.
2. 데이터가 세 개일 때, 버블 정렬 알고리즘 방식으로 정렬해 보자.
3. 데이터가 네 개일 때, 버블 정렬 알고리즘 방식으로 정렬해 보자.

• 데이터가 네 개 일때 (데이터 갯수에 따라 복잡도가 떨어지는 것은 아니므로, 네 개로 바로 로직을 이해해보자.)
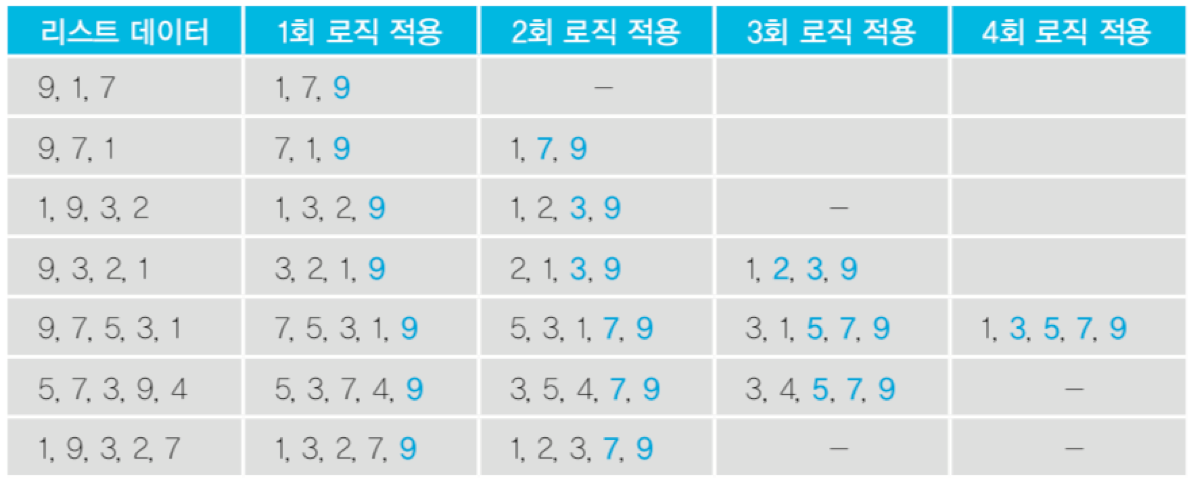
  • 예: data_list = ［1, 9, 3, 2］
    • 1차 로직 적용
      • 1 와 9 비교, 자리바꿈없음 ［1, 9, 3, 2］
      • 9 와 3 비교, 자리바꿈 ［1, 3, 9, 2］
      • 9 와 2 비교, 자리바꿈 ［1, 3, 2, 9］
    • 2차 로직 적용
      • 1 와 3 비교, 자리바꿈없음 ［1, 3, 2, 9］
      • 3 과 2 비교, 자리바꿈 ［1, 2, 3, 9］
      • 3 와 9 비교, 자리바꿈없음 ［1, 2, 3, 9］
    • 3차 로직 적용
      • 1 과 2 비교, 자리바꿈없음 ［1, 2, 3, 9］
      • 2 과 3 비교, 자리바꿈없음 ［1, 2, 3, 9］
      • 3 과 9 비교, 자리바꿈없음 ［1, 2, 3, 9］

알고리즘 구현

• 특이점 찾아보기
  • n개의 리스트가 있는 경우 최대 n-1번의 로직을 적용한다.
  • 로직을 1번 적용할 때마다 가장 큰 숫자가 뒤에서부터 1개씩 결정된다.
  • 로직이 경우에 따라 일찍 끝날 수도 있다. 따라서 로직을 적용할 때 한 번도 데이터가 교환된 적이 없다면 이미 정렬된 상태이므로 더 이상 로직을 반복 적용할 필요가 없다.

1. for num in range(len(data_list)) 반복
2. swap = 0 (교환이 되었는지를 확인하는 변수를 두자)
3. 반복문 안에서, for index in range(len(data_list) - num - 1) n - 1번 반복해야 하므로
4. 반복문안의 반복문 안에서, if data_list［index] > data_list［index + 1] 이면
5. data_list［index], data_list［index + 1] = data_list［index + 1], data_list［index]
6. swap += 1
7. 반복문 안에서, if swap == 0 이면, break 끝

def bubblesort(data):
    for index in range(len(data) - 1):
        swap = False
        for index2 in range(len(data) - index - 1):
            if data[index2] > data[index2 + 1]:
                data[index2], data[index2 + 1] = data[index2 + 1], data[index2]
                swap = True
        
        if swap == False:
            break
    return data

import random

data_list = random.sample(range(100), 50)
print (bubblesort(data_list))

알고리즘 구현2

def bubble_sort(lst):
    n = len(lst)
    for i in range(n):
        for j in range(0, n-i-1):  # 마지막 i 요소는 이미 자리에 있음
            if lst[j] > lst[j+1]:  # 앞의 요소가 더 큰 경우
                lst[j], lst[j+1] = lst[j+1], lst[j]  # 요소들의 위치를 교환
    return lst

# 예제 사용
lst = [64, 34, 25, 12, 22, 11, 90]
bubble_sort(lst)

이 코드는 주어진 리스트 lst를 버블 정렬로 정렬한다. 먼저, 리스트의 길이(n)를 계산한다. 그런 다음 각 요소에 대해 스캔을 시작하며, 매 회전마다 다음 요소와 비교하고 필요한 경우 위치를 바꾼다.

매 회전마다 가장 큰 요소(또는 가장 작은 요소, 내림차순 정렬을 선택한 경우)가 리스트의 끝으로 이동하게 된다. 이것이 버블 정렬의 핵심 원리이다.

bubble_sort 함수는 입력으로 받은 리스트를 직접 수정하며, 정렬된 리스트를 반환한다. 이 예제에서는 [11, 12, 22, 25, 34, 64, 90]이 출력된다.

알고리즘 분석

• 반복문이 두 개 O($n^2$)
  • 최악의 경우, $\frac { n * (n - 1)}{ 2 }$
• 완전 정렬이 되어 있는 상태라면 최선은 O(n)