1. 희소행렬(sparse matrix)의 정의

• 행렬의 대부분의 원소들이 0으로 되어있는 행렬을 말한다.
• 희소행렬을 배열로 표현하면 기억장소의 낭비가 심해서 비효율적이다.
  • linked list로 표현하면 기억장소를 절약할 수 있다.
    
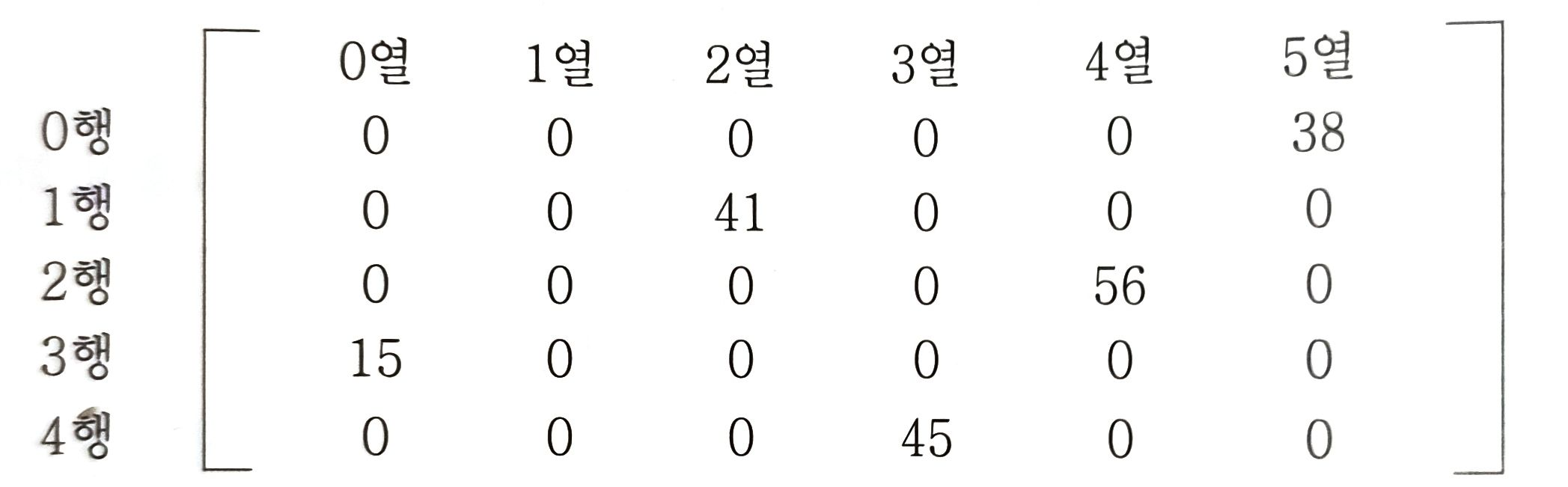
• 위의 5행 6열의 행렬을 2차원 배열로 표현하면 5Ⅹ6=30, 30개의 기억공간이 필요하다.
• 기억장소 절약을 위해서는, 행렬의 크기를 저장한 후에, 희소행렬의 원소 중에서 0이 아닌 원소만을 선택하여 그 값들과 위치(index)를 배열로 저장할 수 있다.
• 통상적으로 전체 원소 중 0이 아닌 원소가 1/3 이하인 경우에 적용하는 것이 효율적이다.
• 희소 행렬은 네트워크, 그래프 혹은 특정 계산에 관련된 데이터 등에서 자주 나타난다.

2. 희소행렬의 2차원 배열 표현

• 희소행렬의 첫 번째 행의 원소인 A(0,0), A(0,1), A(0,2)는 각각 희소행렬의 행의 수, 열의 수, 0이 아닌 원소의 수를 나타낸다.
• 희소행렬은 행의 위치i, 열의 위치j, 원소의 값v를 사용하여 (i, j, v)의 3원소로서 기억시킬 수 있다.
  
• 18개의 기억 공간으로 5행 6열의 희소행렬을 표현한다.