1. 배열(Array)

(1) 정의

• 크기와 성격이 동일한 기억장소가 메모리에 연속적으로 할당되어 데이터를 기억하는 자료구조이다.
• 배열은 서로 같은 데이터 타입을 갖는 여러 항목의 데이터들이 그룹적으로 모여서 하나의 변수이름으로 인덱스에 의해 호출되는 자료구조이며, 배열을 구성하는 항목을 원소(element 또는 member)라고도 한다.
• 배열은 메모리에서 연속적으로 기억되고 직접파일 구조와 비슷한 성격을 가진다.
• 배열의 구성 요소
  • ㉠배열구성요소의 유형 ㉡점차 하한값 ㉢배열명 ㉣배열의 차원

(2) 특징

• 배열은 인덱스와 값의 쌍(인덱스, 값)으로 구성되며, 임의 접근(random access)이 가능한 순차구조로 리스트의 길이를 구하거나, 검색 또는 수정 연산이 많을 때 효율적인 자료구조이다.
• 배열 구조는 삽입과 삭제 시에는 문제가 발생하는데 그 이유는 순차적 사상을 유지하기 위해서 항목의 이동(repacking)연산이 필요하기 때문이다.
• 자료를 저장하고 검색할 때는 각 인덱스에 대응되는 하나의 값을 참조하는 방식으로, 배열명과 첨자로 구별된다.
• 기억장소에 할당되는 배열의 요소번호는 언어에 따라 다르다.
  • 예) C언어는 0부터 시작, 코볼과 포트란은 1부터 시작
• 인덱스는 순서를 나타내는 원소의 유한집합이다.
• 기준주소(α)에서부터 시작하여 연속적인 메모리주소를 할당하여 배열의 논리적순서와메모리의 물리적 순서가 같도록 표현한 것이다.

배열에서의 자료 검색

㉠ 정렬이 안된 배열에서의 임의의 자료검색: O(n)
㉡ 정렬된 배열에서의 임의의 자료검색(이분검색): O(log₂n)
㉢ i번째 자료검색: O(1)

2.배열의 종류

(1) 1차원 배열

• 배열 중에서 가장 단순한 형태로서 벡터(vector)라고도 한다.
• 하나의 첨자를 사용하여 각각의 원소를 표현한다.
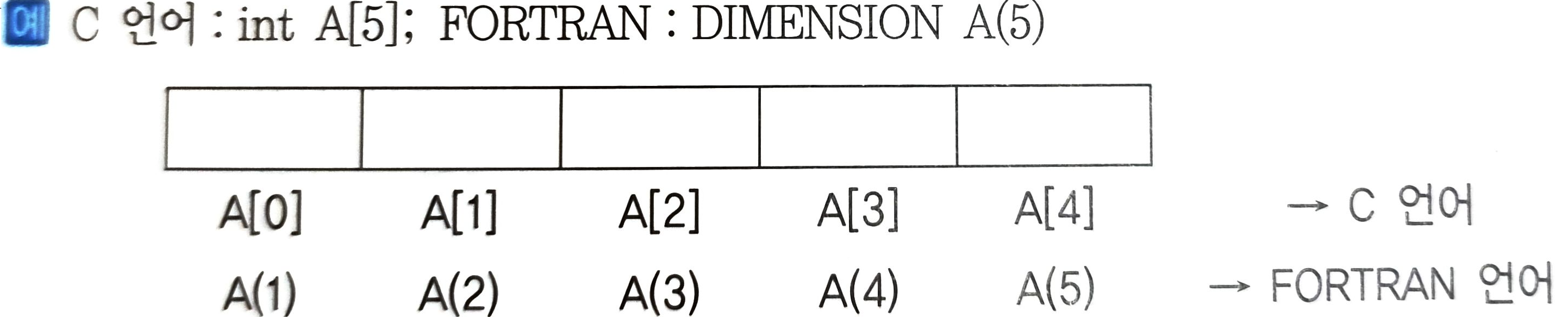
• C언어와 포트란에서 1차원 배열을 선언하는 방법과 배열요소의 관계
  • 
• 그림에서 A는 배열명, 배열을 구성하는 A(i)는 배열 요소
• 특정 배열요소에 대응하는 색인 i를 첨자라 하는데, 첨자는 포트란이나 코볼에서는 배열의 인덱스가 1부터 시작되지만, C언어에서는 0부터 시작된다.
• 참고로 베이직(Basic)에서는 intA[5]라 선언하면 A[0]~A[5]까지 6개의 배열 요소가 만들어진다.
• 일차원 배열에서 A(1)의 주소가 α라면 임의의 A(i)의 위치는 A(i) = α + (i - 1)이다. 즉, 일차원 배열에서 임의 원소의 주소 계산은 시작주소 + 원소의 위치 - 1 이다.
• 배열의 색인 범위는 하한(lower bound)과 상한(upper bound)으로 정의될 수 있는데 하한의 값이 포트란에서는 1, C에서는 0으로 고정. Pascal에서는 하한과 상한의 값을 임의 정수로 설정한다.
  • Pascal에서 배열을 선언한 예
    • Var A:Array[2..5] of Integer; 배열요소는 A[2], A[3], A[4], A[5]가 된다.
• 배열 A[l...u]의 각 원소가 k개의 기억장치 단위를 차지한다면, 이 배열의 크기는(u-l+1)k가 된다.

(2) 다차원 배열

• 이차원 이상의 배열로, 두 개 이상의 첨자를 이용하여 각 원소와 대응시키는 방법이다.
• 1차원 배열 전체가 하나의 배열요소가 될 수 있고, 배열의 배열이다.
• 1차원 배열의 물리적인 저장은 논리적 순서와 같으나 다차원 배열 저장 기법은 행 중심(row major)방식과 열 중식(column major)방식이 있다.

(3) 2차원 배열

1) 정의

• 2차원 배열은 같은 크기를 갖는 1차원 배열이 여러개 모여서 구성된 배열로서, 행렬(matrix)이라고 한다.
• 행렬에서 가로줄의 벡터를 행(row), 세로줄의 벡터를 열(column)이라고 하며, 행이 m개이고 열이 n개일 때 이 행렬의 크기는 mn이다.
  • 다음은 2행 3열 구조를 갖는 2차원 배열구조이다.

	1열	2열	3열
1행	A(1,1)	A(1,2)	A(1,3)
2행	A(2,1)	A(2,2)	A(2,3)

• 2차원 배열을 기억장소에 배치하는 방법: 행우선 방식과 열우선 방식
  • 행우선: COBOL, C, PASCAL, PL/1 등
  • 열우선: FORTRAN
    • 다음은 2차원 배열이 실제로 기억장소에 배치되는 모습이다.

행우선일때	A(1,1)	A(1,2)	A(1,3)	A(2,1)	A(2,2)	A(2,3)	→ COBOL
열우선일때	A(1,1)	A(2,1)	A(1,2)	A(2,2)	A(1,3)	A(2,3)	→ FORTRAN

2) 2차원 배열의 위치

• 2차원 배열 A[i,j]의 위치를 구하는 공식, 배열 원소: A[1:m, 1:n], α:A[1:1]의 주소
  • 행 중심 A[i, j]: α + (i-1)n + (j-1)
  • 열 중심 A[i, j]: α + (j-1)m + (i-1)
    
• 배열 A[l₁..u₁,l₂...u₂]를 나타낼 때 원소 A[i,j]의 주소 (k는 배열 구성 원소의 크기)
  • 행우선 A[i,j]:address(A[l₁,l₂]) + (i-l₁)(u₂-l₂+1)k+(j-l₂)k
  • 열우선 A[i,j]:address(A[l₁,l₂]) + (j-l₂)(u₁-l₁+1)k+(i-l₁)l
    

(4) 3차원 배열

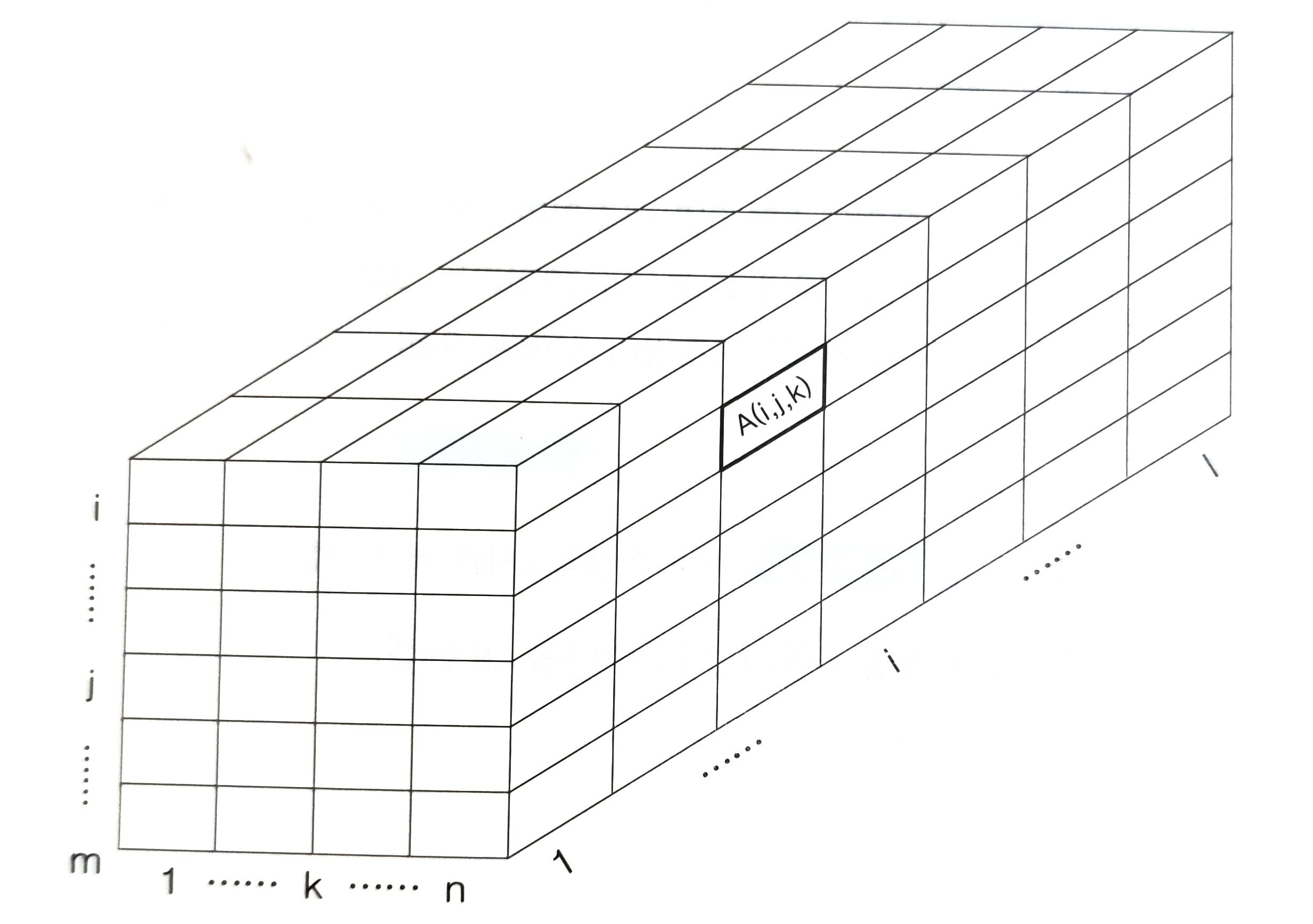
3차원 배열은 n개의 2차원 배열로 구성되며 면, 행, 열이라는 3개의 첨자를 이용하여 각각의 원소에 대응된다.

• 3차원 배열 A(l,m,n)에서 시작위치 A(1,1,1)를 α라고 할 때, A(i,j,k)의 위치를 구하는 공식
  • 행우선: α + (i-1)mn + (j-1)n + (k-1)
  • 열우선: α + (i-1)mn + (k-1)m + (j-1)
• 3차원 배열 A(l,m,n)에서 시작주소 A(0,0,0)를 α라고 할 때, A(i,j,k)의 위치를 구하는 고잇ㄱ
  • 행우선: α + imn + jn + k
  • 열우선: α + imn + kn + j
• 3차원 배열 A[l₁..u₁, l₂..u₂, l₃..u₃]은 3차원의 입체 공간이다.
  • 총 원소의 개수는 (u₁- l₁+1)(u₂- l₂+1)(u₃- l₃+1)
  • 예) 배열 A[l₁..u₁, l₂..u₂, l₃..u₃]의 일반 원소 A[p,q,r]의 주소는 다음과 같다. (k는 배열 A의 각 원소가 차지하는 기억장소의 크기이다.)
  • 행 우선일 경우: A[p,q,r]: address (A[l₁, l₂, l₃]) + (p-l₁)(u₂-l₂+1)(u₃-l₃+1)k + (q-l₂)(u₃-l₃+1)k + (r-l₃)k
  • 열 우선일 경우: A[p,q,r]: address (A[l₁, l₂, l₃]) + (p-l₁)(u₂-l₂+1)(u₃-l₃+1)k + (r-l₃)(u₂-l₂+1)k + (q-l₂)k