그래프

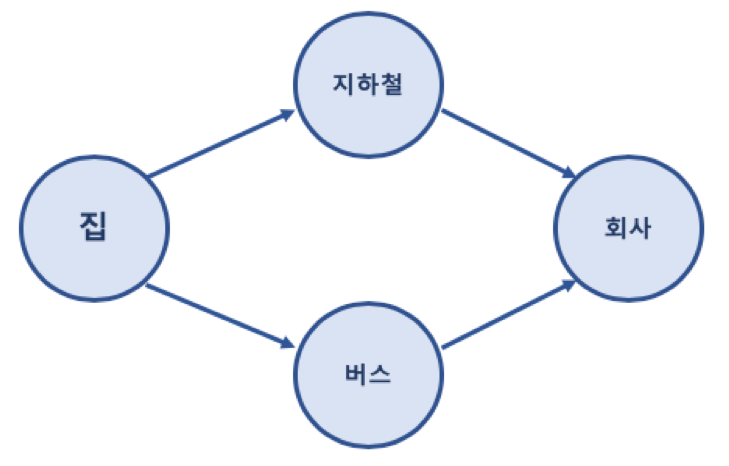
그래프는 여러 노드(Node)들이 여러 간선(Edge)에 의해 연결되어 있는 구조를 말한다. 그래프는 실제 세계의 여러 문제 상황을 모델링하기 위해 사용되며, 컴퓨터 과학 및 여러 응용 분야에서 널리 활용되고 있다.

그래프의 요소

1. 노드(Node 또는 Vertex): 그래프의 개별 요소를 나타낸다. 위치로 생각할 수 있다. 예를 들면, 도시, 컴퓨터, 정점 등을 표현할 수 있다.
2. 간선(Edge): 두 노드를 연결하는 선으로, 노드(위치) 간의 관계를 나타낸다. 간선은 가중치를 가질 수 있다.
3. 인접 정점(Adjacent Vertex): 간선으로 직접 연결된 정점(또는 노드)
4. 차수(Degree): 한 노드에 연결된 간선의 수를 나타낸다. 무방향 그래프에서 노드의 차수는 그 노드에 인접한 노드의 수와 같다.
5. 경로(Path): 두 노드를 연결하는 간선의 연속이다. 경로의 길이는 그 경로에 포함된 간선의 수를 의미한다.
6. 사이클(Cycle): 시작 노드와 끝 노드가 동일한 경로를 말한다.
7. 방향 그래프(Directed Graph 또는 Digraph): 간선에 방향이 있는 그래프다.
8. 무방향 그래프(Undirected Graph): 간선에 방향이 없는 그래프다.
9. 가중치(Weight): 간선에 할당된 값이다. 거리, 비용, 시간 등 다양한 것을 표현할 수 있다.
10. 연결 그래프(Connected Graph): 무방향 그래프에서 모든 노드 쌍에 대해 어떤 경로가 존재하면 연결 그래프라고 한다.
11. 강 연결 그래프(Strongly Connected Graph): 방향 그래프에서 모든 노드 쌍에 대해 어떤 경로가 존재하면 강 연결 그래프라 한다.
12. 서브그래프(Subgraph): 그래프의 일부 노드와 그 노드들을 연결하는 간선으로 이루어진 그래프다.

그 외에 참고할 만한 용어는 다음과 같다.

• 정점의 차수 (Degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
• 진입 차수 (In-Degree): 방향 그래프에서 외부에서 오는 간선의 수
• 진출 차수 (Out-Degree): 방향 그래프에서 외부로 향하는 간선의 수
• 경로 길이 (Path Length): 경로를 구성하기 위해 사용된 간선의 수
• 단순 경로 (Simple Path): 처음 정점과 끝 정점을 제외하고 중복된 정점이 없는 경로

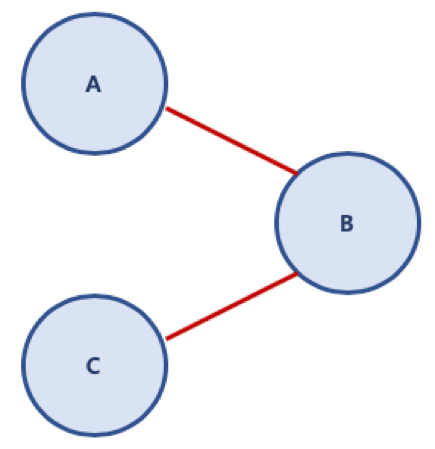
△ 단순 경로 그래프

그래프의 종류

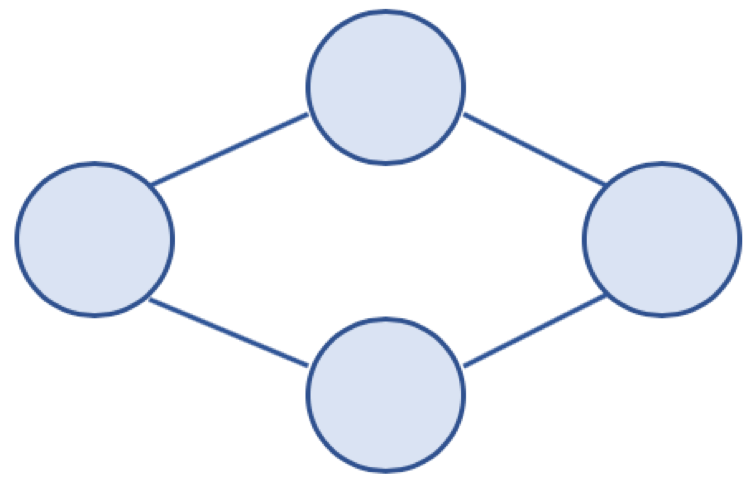
무방향 그래프(Undirected Graph)

• 간선에 방향이 없는 그래프다. 두 노드는 서로 연결되어 있다.
• 간선을 통해, 노드는 양방향으로 갈 수 있다.
• 보통 노드 A, B가 연결되어 있을 경우, (A, B) 또는 (B, A) 로 표기

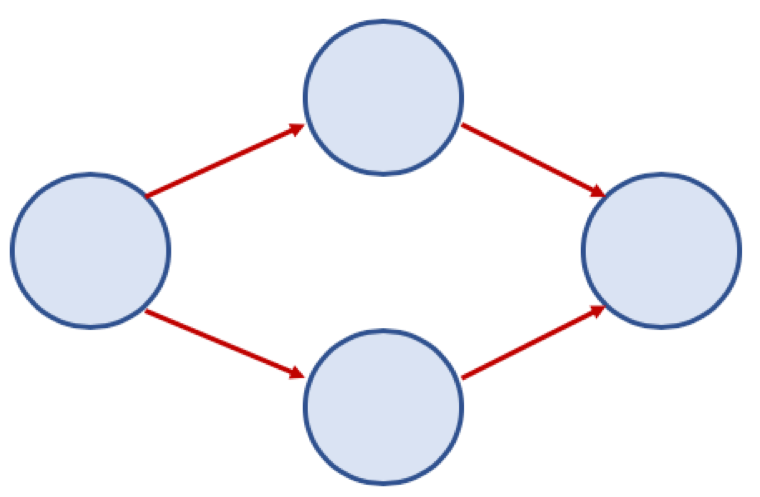
방향 그래프 (Directed Graph)

• 간선에 방향이 있는 그래프다. 간선은 시작 노드에서 끝 노드로 방향을 가진다.
• 보통 노드 A, B가 A -> B 로 가는 간선으로 연결되어 있을 경우, <A, B> 로 표기 (<B, A> 는 B -> A 로 가는 간선이 있는 경우이므로 <A, B> 와 다름)

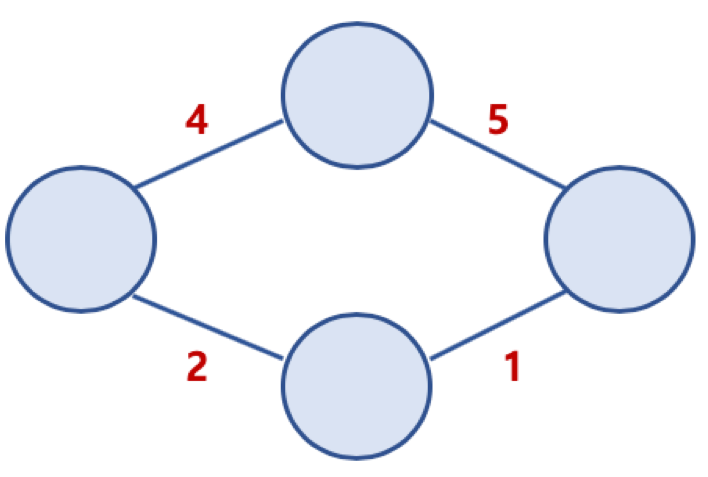
가중치 그래프(Weighter Graph) 또는 네트워크(Network)

• 각 간선에 가중치 또는 비용이 할당된 그래프를 의미한다.
• 가중치는 거리, 시간, 비용 등 다양한 것을 표현할 수 있다.

연결 그래프(Connected Graph)와 비연결 그래프(Disconnected Graph)

• 연결 그래프(Connected Graph)
  • 무방향 그래프에서 임의의 두 노드 사이에 항상 경로가 존재하면 연결 그래프라고 한다. 즉, 그래프 내의 모든 노드가 서로 연결되어 있다면 연결 그래프이다.
• 비연결 그래프(Disconnected Graph)
  • 무방향 그래프에서 임의의 두 노드 사이에 경로가 존재하지 않는 경우가 있으면 비연결 그래프라고 한다. 그래프 내의 모든 노드가 서로 연결되어 있지 않을 때를 의미한다.

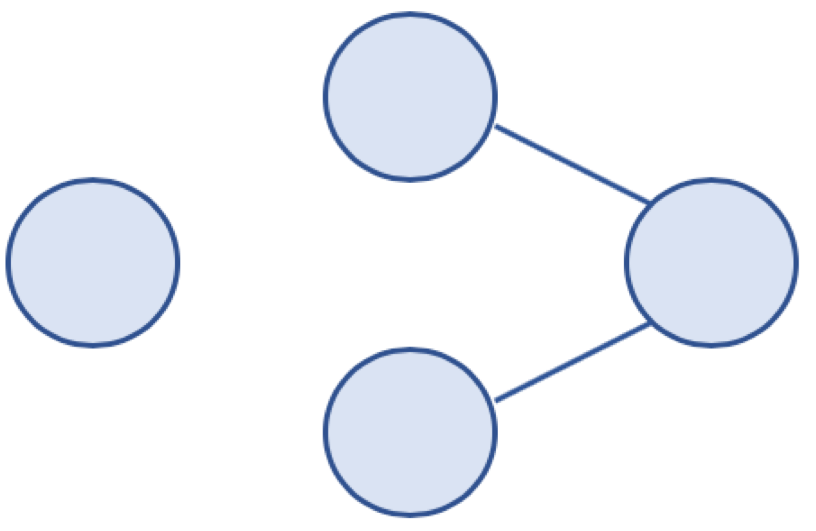
△ 비연결 그래프

사이클(Cycle)과 비순환 그래프(Acyclic Graph)

• 사이클(Cycle)
  • 단순 경로의 시작 노드와 종료 노드가 동일한 경우
• 비순환 그래프(Acyclic Graph)
  • 사이클이 없는 그래프

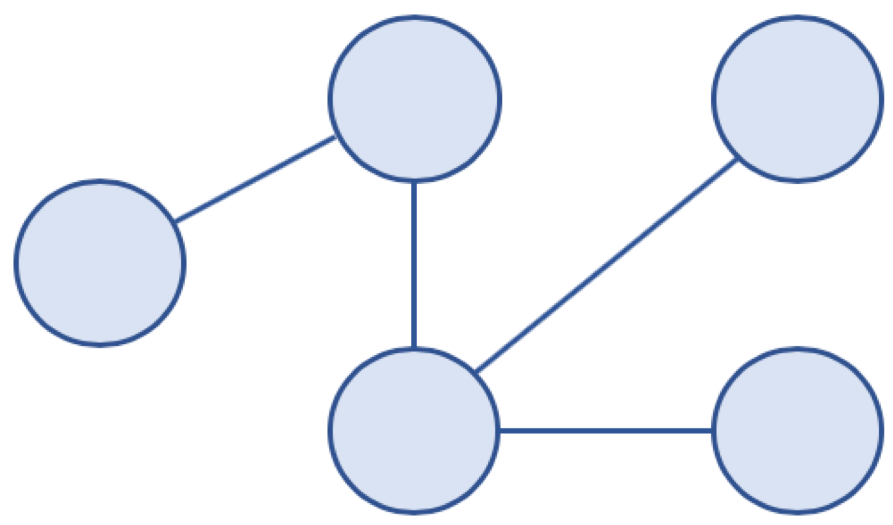
△ 비순환 그래프

완전 그래프(Complete Graph)

• 그래프의 모든 노드가 서로 연결되어 있는 그래프
• n개의 노드가 있는 완전 그래프의 간선의 수는 n(n-1)/2이다.

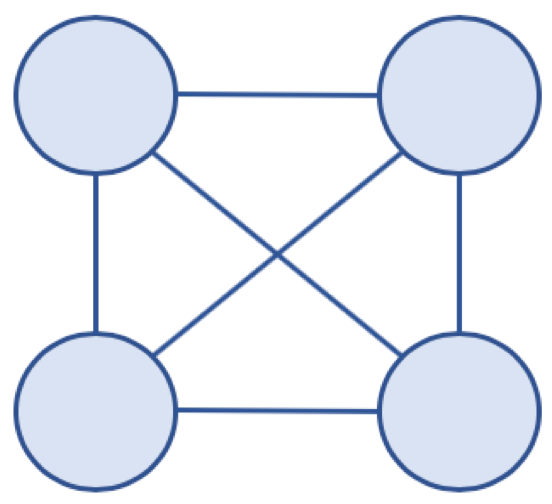
△ 완전 그래프

그래프와 트리의 차이

	그래프	트리
정의	노드와 노드를 연결하는 간선으로 표현되는 자료 구조	그래프의 한 종류, 방향성이 있는 비순환 그래프
방향성	방향 그래프, 무방향 그래프 둘다 존재함	보통 방향성을 가지며, 루트 노드에서 다른 노드들로 방향성을 가진다.
사이클	사이클 가능함, 순환 및 비순환 그래프 모두 존재함	비순환 그래프로 사이클이 존재하지 않음
루트 노드	루트 노드 존재하지 않음	루트 노드 존재함
부모/자식 관계	부모 자식 개념이 존재하지 않음	부모 자식 관계가 존재함
간선의 수	제한 없음	'n'개의 노드가 있을 때, 'n-1'개의 간선이 있다.
사용하는 곳	네트워크 모델링, 경로 찾기 등 다양한 분야에서 사용된다.	계층적 데이터를 표현할 때 사용된다. 예를 들면, 파일 시스템, DOM(Document Object Model) 구조 등에서 사용된다.