깊이 우선 탐색 (Depth-First Search)

DFS란?

깊이 우선 탐색 (Depth-First Search, DFS)은 그래프의 모든 노드를 방문하는 알고리즘 중 하나이다. DFS는 현재 노드와 인접한 노드를 재귀적으로 탐색하며, 그래프의 깊숙한 곳까지 우선 탐색한다. 이런 방식 때문에 "깊이 우선"이라는 이름이 붙었다.

DFS의 기본 원리 및 작동 방식

1. 시작 노드를 방문한다.
2. 현재 노드를 '방문 처리'한다. (일반적으로 리스트나 셋을 사용하여 방문 처리)
3. 현재 노드와 연결된 아직 방문하지 않은 인접 노드를 확인하고, 방문하지 않은 인접 노드가 있으면 그 노드를 시작 노드로 하여 위의 과정을 반복한다.
4. 모든 인접 노드를 방문했다면 (즉, 더 이상 방문할 노드가 없다면) 이전 노드로 돌아간다.
5. 위의 과정을 모든 노드를 방문할 때까지 반복한다.

DFS방식의 예제

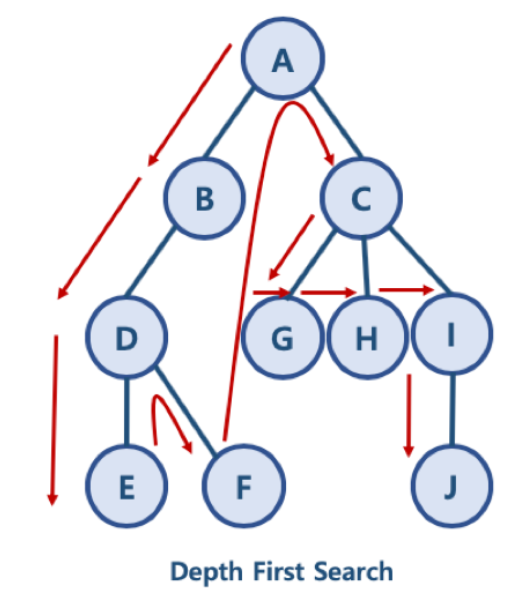
DFS방식은 한 노드의 자식을 타고 끝까지 순회한 후, 다시 돌아와서 다른 형제들의 자식을 타고 내려가며 순회한다.ㅈ

파이썬으로 그래프를 표현하는 방법

파이썬에서 제공하는 딕셔너리와 리스트 자료 구조를 홀용하여, 그래프를 포현할 수 있다.

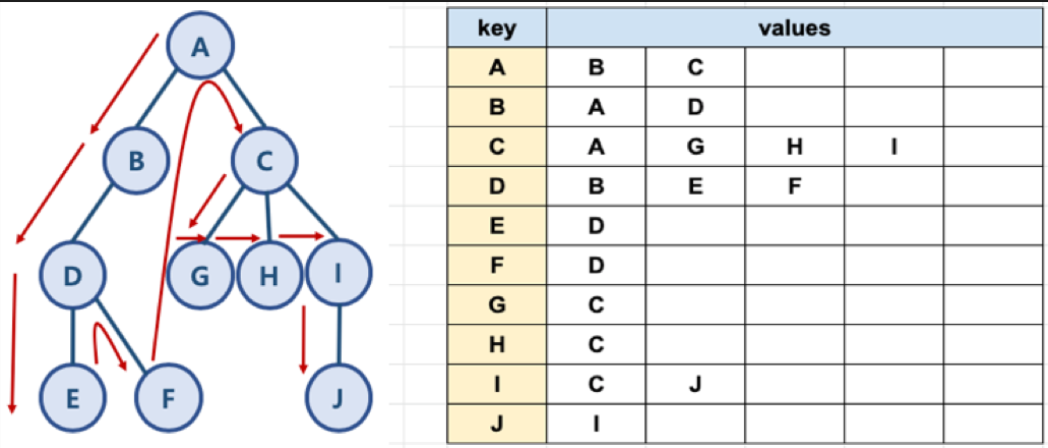
graph = dict()

graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']

graph
"""
{'A': ['B', 'C'],
 'B': ['A', 'D'],
 'C': ['A', 'G', 'H', 'I'],
 'D': ['B', 'E', 'F'],
 'E': ['D'],
 'F': ['D'],
 'G': ['C'],
 'H': ['C'],
 'I': ['C', 'J'],
 'J': ['I']}
"""

파이썬으로의 기본적인 DFS 구현 예시

DFS는 스택을 사용하여 구현될 수 있다. 재귀 함수를 사용하는 방법도 사실상 시스템 스택을 사용하는 것이므로, 재귀를 이용한 구현도 DFS의 일종이다.

def dfs(graph, v, visited):
    # 현재 노드를 방문 처리
    visited[v] = True
    print(v, end=' ')
    
    # 현재 노드와 연결된 다른 노드를 재귀적으로 방문
    for i in graph[v]:
        if not visited[i]:
            dfs(graph, i, visited)

# 각 노드가 연결된 정보를 표현 (2차원 리스트)
graph = [
    [],        # 0번 노드는 없다고 가정
    [2, 3, 8], # 1번 노드와 연결된 노드들
    [1, 7],    # 2번 노드와 연결된 노드들
    # ...
]

# 각 노드가 방문된 정보를 표현 (1차원 리스트)
visited = [False] * 9  # 인덱스 0은 사용하지 않기 위해

# 정의된 DFS 함수 호출
dfs(graph, 1, visited)

DFS 알고리즘 구현

• 자료구조 스택과 큐를 활용한다.
  • need_visit스택과 visited 큐, 두 개의 자료 구조를 생성
• 밑처럼, 간단한 파이썬 리스트를 활용하여 만들 수 도 있다.

def dfs(graph, start_node):
    visited, need_visit = list(), list()
    need_visit.append(start_node)
    
    while need_visit:
        node = need_visit.pop()
        if node not in visited:
            visited.append(node)
            need_visit.extend(graph[node])
    
    return visited

코드의 동작 방식을 단계별로 살펴보자.

1. 초기 설정
   visited: 이미 방문한 노드들을 저장하는 리스트입니다. 초기에는 빈 리스트로 시작한다.
   need_visit: 아직 방문하지 않았지만 방문해야 할 노드들을 저장하는 리스트입니다. 시작 노드가 이 리스트에 초기값으로 들어간다.
2. 탐색 시작
   need_visit 리스트에 값이 있는 동안, 즉 아직 방문해야 할 노드가 남아 있는 동안 반복문을 계속 실행한다.
3. 노드 탐색
   need_visit에서 마지막 노드를 꺼내 node 변수에 저장한다.
   만약 해당 노드가 visited 리스트에 없다면, 즉 아직 방문하지 않은 노드라면 visited 리스트에 추가한다.
4. 다음 방문 대상 탐색
   현재 노드와 직접 연결된 노드들 (인접 노드)을 need_visit 리스트에 추가한다.
   여기서 extend 함수를 사용하면, 해당 노드의 인접 노드들을 모두 need_visit 리스트에 추가하게 된다.
5. 결과 반환
   모든 노드를 방문하게 되면 while 반복문이 종료되고, visited 리스트가 반환됩니다. 이 리스트에는 탐색한 노드들이 DFS 방식에 따라 순서대로 저장되어 있다.

이러한 방식으로 DFS를 반복문을 사용하여 구현하게 되면, 재귀를 사용한 DFS에 비해 스택 오버플로우의 위험이 없으므로 대규모 그래프에 대해서도 안정적으로 탐색이 가능하다.

그러나 이 코드의 방식은 전통적인 재귀를 사용한 DFS와는 약간 다른 방식이므로, 특정 문제 상황에 따라서는 결과의 순서가 달라질 수 있다.

이 DFS 알고리즘은 노드의 수가 V, 간선의 수가E일 때, 시간 복잡도는 인접 리스트 방식으로 표현된 그래프일 경우 $O(V + E)$이다.
(코드에서, while need_visit은 V+E번 만큼 수행해야 한다.)