평균-분산 최적화(Mean-Variance Optimization)

HKK·2022년 11월 24일

Finance AI

목록 보기

2/5

Mean-Variance Optimization

n개의 자산으로 구성된 어떤 포트폴리오의 기대수익률과 분산은 아래와 같이 나타낼 수 있다.

E(R_p)=\Sigma _iw_iE(R_i),\ \ \ \ \sigma _p^2=\Sigma _i\Sigma _jw_iw_j\sigma _i\sigma _j\rho _{ij}

위와 같이 자산 i의 기대수익률을 $E(R_i)$ , 포트폴리오 가중치를 $W_i$ 라고 할때, 두가지 포트폴리오에 대해 생각해보자. 첫번째 포트폴리오A는 하나의 자산에만 투자하는 것으로 w1=1이고 나머지 n-1개의 자산의 가중치는 0이되는 경우이다. 그리고 두번째 포트폴리오B는 모든 자산의 가중치가 1/n으로 동일한 포트폴리오이다. 그리고 각각의 포트폴리오A,B는 다음과 같은 기대수익률과 분산을 가지게 된다.

E[R_A] =E[R_B]=\mu \\ Var(R_A)=\sigma ^2 \\ Var(R_B)=\sigma ^2/n

포트폴리오 A,B는 도일한 기대수익률을 가지지만 분산은 다르다. 만약 운용 매니저라면 어떤 포트폴리오를 선택할 것인가? 아마도 분산이 작은 포트폴리오 B를 선택해 리스크를 줄이고자 할 것이다. 이것이 마르코위츠가 제안한 MVO(Mean-Variance Optimization)의 핵심아이디어로 기대수익률이 동일할때 분산을 최소화 하고, 분산이 동일할때는 기대수익률을 최대화 하는 것이다.

MVO의 notation은 아래와 같은데, 앞서 말한것과 같이 분산을 최소화하는 방법과 기대수익률을 최대화 하는 방법이 있다. 그리고 이때 람다는 투자자의 위험회피성향으로 투자자가 직접 설정하는 것으로 위험회피성향이 커질수록 우리가 최대화할 목적함수는 적어진다. 왜냐하면 위험감수 능력이 떨어지는 투자자일수록 안전한 투자를 원하기 때문에 그만큼 risk premium은 적어질 수 밖에 없기 때문이다.

Minimum Variance Portfolio

\min _w^{ }\frac{\lambda }{2}w^T\Sigma w \\ subject\ to\ w^T\mu =p \\ \text{and}\ \ \ \Sigma w_i=1

\max _w^{ }\ \ \ w^T\mu -\frac{\lambda }{2}w^T\Sigma w\\ subject\ to\ \ \ \Sigma w_i=1

보편적으로는 기대수익률을 최대화 하는 경우를 MVO모델로 많이 사용하는데 해당 목적함수를 풀기 위해서는 가중치 w에 대해 미분하면 되고, MVO의 최종해는 다음과 같다.

w=(\lambda \Sigma )^{-1}\mu

MVO는 위의 notation에서 볼 수 있듯이 매우 간결한 모델이다. 물론 해당 모델은 제시되었던 1950년대에는 투자자산이 금, 채권, 주식 정도였기 때문에 유의미했다고 보지만 현대에는 자산군의 범위가 넓어졌을 뿐만 아니라 자산간 상관성도 커졌고 macro 변동성도 커졌기 때문에 앞으로 접목시키기에는 한계점이 있는것으로 보인다.

Eficient Frontier

이전 포스팅에서 평균-분산 최적화 개념을 소개한적이 있다. 해당개념은 현대 포트폴리오 이론에서 아주 기초적인 부분으로, 포트폴리오의 분산을 최적화해 리스크를 최소화 시킨다는 개념이다. 그리고, 이 개념에서 파생된 개념인 효율적 프론티어에 대해 설명하고, 이를 파이썬으로 구현하는 작업을 진행하겠다.

효율적 프론티어(Efficient Frontier)는 포트폴리오 리스크의 최대 수준을 감안할 때 포트폴리오 수익률을 최대로 하는 포트폴리오를 뜻한다. 자산들의 조합인 포트폴리오는, 자산에 따른 변동과 포트폴리오의 변동이 존재한다.

하지만, 이러한 포트폴리오 변동(리스크)은 자산을 적절하게 배분함으로써 줄일 수 있는데, 여기서 '적절한'을 찾는것이 곧 효율적 프론티어를 찾는것이고, 평규-분산 최적화 기법을 활용해서 찾을 수 있게 되는것이다. 효율적 프론티어 계산을 위해서는 각 자산의 기대수익률, 변동성 그리고 자산간의 공분산을 계산해 이들의 변동성을 최소화하고 기대수익률을 최대화 하는 가중치를 계산함으로써 우리는 효율적 프론티어를 찾을 수 있다.

포트폴리오 전체 분산(리스크)는 자산들의 variance-covariance matrix와 가중치 제곱의 합으로 계산된다.

\sigma _{PF}=w^T\Sigma w

포트폴리오 리스크를 최적화하는 문제는 목표기대수익률하에서 포트폴리오 리스크를 최소화하는 것과 동등하다.

\min _w^{ }\ \ \sigma _{PF}^2=w^T\Sigma w \\ s.t.\ \ \ w^T\mu =\sigma _{PF}

Efficient Frontier for Python

해당 실험은 두가지 파트로 나뉘는데 첫번째로는 100,000개의 서로 다른 가중치를 접목시켜 각각의 표준편차와 수익률을 찾고, volatility 최소값과 sharp ratio의 최대값을 찾는다. 그리고, 해당값들을 최적화 하는 문제를 풀어 efficient portfolio를 찾게된다.

Part1. Simulation

우선, scipy.optimize의 minimize함수를 import하고, 구성하고자 하는 포트폴리오 종목 10종목을 선정해 데이터를 만들었다.

import pandas as pd
import numpy as np
from numpy.random import random, uniform, dirichlet, choice
from numpy.linalg import inv

from scipy.optimize import minimize

import pandas_datareader.data as web
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter

!pip install yfinance
import yfinance as yf
import plotly.graph_objects as go

import pandas as pd
import numpy as np
from numpy.random import random, uniform, dirichlet, choice
from numpy.linalg import inv

from scipy.optimize import minimize

import pandas_datareader.data as web
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter

!pip install yfinance
import yfinance as yf
import plotly.graph_objects as go

ticker = ['005380.KS','005930.KS','DIS','AAPL','MSFT','SPY','NKE','035720.KS','005490.KS','008770.KS']
df = yf.download(ticker,start='2012-08-16',end = '2022-08-16')[['Close']]
df = df.dropna()
df.columns = ['현대차','삼성전자','디즈니','애플','마소','SnP','나이키','카카오','POSCO','호텔신라']
df = np.log(df).pct_change()
df = df.dropna()

그리고, 파라미터 세팅작업을 시행한다. 파라미터로는 시뮬레이션에 필요한 작업횟수 NUM_PF, 초기값 x0가 있고, 평균 수익률, covariance matrix, 무위험이자율 등은 포트폴리오 성과 측정에 필요한 파라미터이다.


#파라미터 셋팅
stocks = df.columns
n_obs, n_assets = df.shape
NUM_PF = 100000 #number of portfolios to simulate

x0 = uniform(0, 1, n_assets) #초기값
x0 /= np.sum(np.abs(x0))

#연단위 환산
periods_per_year = round(df.resample('A').size().mean())
periods_per_year #전체 기간을 1년 단위로 환산

#무위험이자율: 미국 10년 국고채
treasury_10yr = yf.download('^TNX',start='2021-08-16',end = '2022-08-16')[['Close']]
rf_rate = treasury_10yr.mean()

#평균 수익률 및 covariance-variance matrix
mean_returns = df.mean()
cov_matrix = df.cov()

#precision matrix는 covariance matrix의 inverse matrix
precision_matrix = pd.DataFrame(inv(cov_matrix), index=stocks, columns=stocks) 
precision_matrix

다음으로 시뮬레이션한 포트폴리오들의 평균, 표준편차 그리고 샤프 비율을 계산한다. 단, 평균과 표준편차를 계산할때는 연율화 작업을 진행한다.

def simulate_portfolios(mean_ret, cov, rf_rate=rf_rate, short=True):
  alpha = np.full(shape=n_assets, fill_value = .05) #alpha값은 모두 일정하게 0.05
  weights = dirichlet(alpha = alpha, size = NUM_PF) #디리클레 분포로 가중치 생성 (NUM_PF 갯수만큼)
  
  if short:
    weights *= choice([-1,1], size=weights.shape) #무작위로 가중치 선정

  returns = weights @ mean_ret.values + 1 #weights vector, mean return matrix multiplication
  returns = returns ** periods_per_year - 1 #전체 평균을 하루짜리로
  std = (weights @ df.T).std(1) #행 하나씩(weight 하나씩) std 계산
  std *= np.sqrt(periods_per_year) #연율화: 연율화는 루트 씌워야함
  sharpe = (returns - rf_rate.to_numpy()) / std

  return pd.DataFrame({'Annualized Standard Deviation': std,
                       'Annualized Returns': returns,
                       'Sharpe Ratio': sharpe}), weights
                       
simul_perf, weights = simulate_portfolios(mean_returns, cov_matrix, short=False)

이렇게 시뮬레이션된 포트폴리오의 최소 변동성(표준편차)값, 최대 샤프비율을 시각화 하면 아래와 같다. x축은 연율화한 표준편차이고, y축은 연율화한 수익률이다. 각 양 끝점에는 sharp ratio의 최대값과 volatility 최소값이 위치하고 있다. 이렇게 각각의 시뮬레이션을 통해 수익률과 표준편차를 구했으니 변동성을 최소화 하는 efficient frontier를 찾아보겠다.

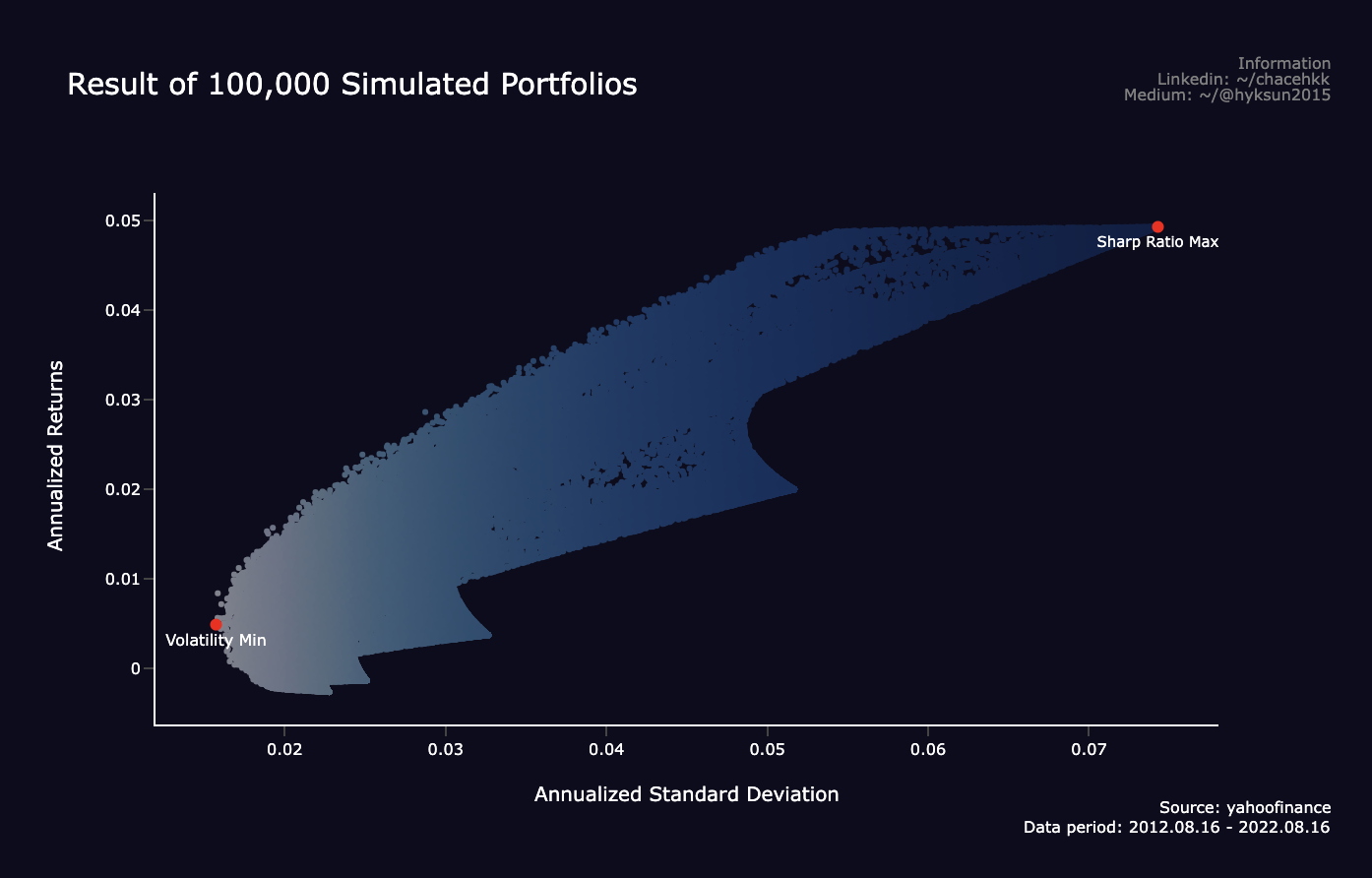
Part2. Simulation

우선, 위와 동일하게 포트폴리오 시뮬레이션을 진행합니다.
(위의 simul_perf, simul_wt 를 사용하여도 무방합니다.)

simul_perf, simul_wt = simulate_portfolios(mean_returns, cov_matrix, short=False)
simul_max_sharpe = simul_perf.iloc[:,2].idxmax()
simul_perf.iloc[simul_max_sharpe]

다음으론 포트폴리오의 최대 샤프 비율을 구합니다. 최대 샤프 비율을 구하는데는 sharp ratio의 음수를 최소화 하는 것으로 최적화를 진행하게 됩니다.

def portfolio_std(wt, rt=None, cov=None):
    return np.sqrt(wt @ cov @ wt * periods_per_year)

def portfolio_returns(wt, rt=None, cov=None):
    return (wt @ rt + 1) ** periods_per_year -1

def portfolio_performance(wt, rt, cov):
    r = portfolio_returns(wt, rt=rt)
    sd = portfolio_std(wt, cov=cov)
    return r, sd
    
#minimize function
def neg_sharpe_ratio(weights, mean_ret, cov):
    r, sd = portfolio_performance(weights, mean_ret, cov)
    return -(r - rf_rate) / sd

def max_sharpe_ratio(mean_ret, cov, short=False):
    return minimize(fun=neg_sharpe_ratio, #제약식
                    x0=x0, #초기값
                    args=(mean_ret, cov),
                    method='SLSQP',
                    bounds=((0, 1),) * n_assets, #weight가 0,1 사이에 오도록
                    constraints = {'type':'eq','fun': lambda x: np.sum(np.abs(x))-1}, #weight의 합이 1
                    options={'maxiter':1e4}) #최대 반복 횟수
                    
# get max sharpe PF
max_sharpe_pf = max_sharpe_ratio(mean_returns, cov_matrix, short=False)
max_sharpe_perf = portfolio_performance(max_sharpe_pf.x, mean_returns, cov_matrix)

그리곤, 최소분산 포트폴리오를 찾습니다. 최소분산 포트폴리오는 리스크 최소화를 가장 최우선으로 하는 포트폴리오로 시뮬레이션된 포트폴리오 중 가중치가 [0,1]로 제한되고 합이 절대적으로 1이 되는 제약조건을 만족하며 표준편차가 최소인 포트폴리오가 최소분산포트폴리오로 선정됩니다.

def min_vol(mean_ret, cov, short=False):

    return minimize(fun=portfolio_std,
                    x0=x0,
                    args=(mean_ret, cov),
                    method='SLSQP',
                    bounds = ((0, 1),) * n_assets,
                    constraints={'type':'eq','fun': lambda x: np.sum(np.abs(x))-1},
                    options={'maxiter': 1e4})
                    
#get minvol PF
min_vol_pf = min_vol(mean_returns, cov_matrix, short=False)
min_vol_perf = portfolio_performance(min_vol_pf.x, mean_returns, cov_matrix)

마지막으로 efficient frontier를 구하게 됩니다. 목표 수익률의 범위를 반복하고 대응되는 최소 분산포트폴리오를 효율적 프론티어로 계산한다. 이를 위해 포트폴리오의 리스크와 수익률의 제약조건을 가중치로 최적화 문제를 풀게된다.

def min_vol_target(mean_ret, cov, target, short=False):

    def ret_(wt):
        return portfolio_returns(wt, mean_ret)

    return minimize(portfolio_std,
                    x0=x0,
                    args=(mean_ret, cov),
                    method='SLSQP',
                    bounds = ((0, 1),) * n_assets,
                    constraints = [{'type': 'eq','fun': lambda x: ret_(x) - target}
                                   ,{'type':'eq','fun': lambda x: np.sum(np.abs(x))-1}], #합계=1
                    options={'maxiter': 1e4})
                    
def efficient_frontier(mean_ret, cov, ret_range, short=False):
    return [min_vol_target(mean_ret, cov, ret) for ret in ret_range]
    
    
#get efficient PF
ret_range = np.linspace(simul_perf.iloc[:, 1].min(), simul_perf.iloc[:, 1].max(), 50)
eff_pf = efficient_frontier(mean_returns, cov_matrix, ret_range, short=True)
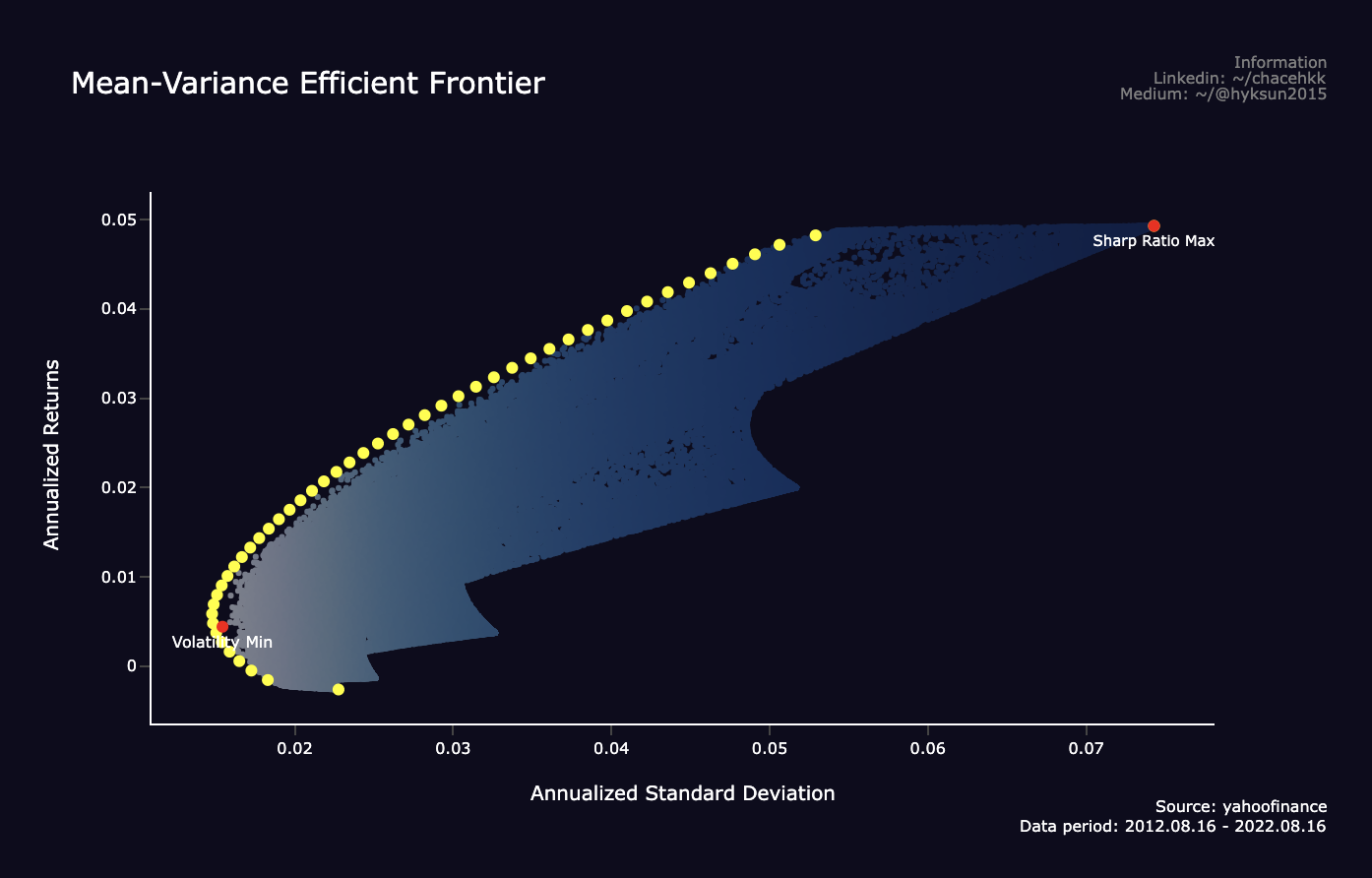
eff_pf = pd.Series(dict(zip([p['fun'] for p in eff_pf], ret_range)))

그리고 이렇게 평균수익률과 분산을 최적화 시킨 효율적 프론티어는 다음과 같이 그려진다. 그림에서 볼 수 있듯이 수익률과 변동성은 서로 트레이드 오프 관계이다. 즉, 수익률이 좋으면 리스크가 크고 리스크가 작으면 수익률이 하락한다.

이러한 트레이드 오프를 고려했을때 포트폴리오 매니저는 본인 포트폴리오 전략에 맞게 리스크를 감수하고 수익률을 극대화 하거나, 리스크를 최소화 한다던가 아니면 그 사이 어딘가에서 포트폴리오 비율을 조정하면 된다. 그러나... 그림에서 볼 수 있듯이 최대 수익률이라고 해봤자 5%정도 밖에 안되므로.. 이 경우 종목선정 자체가 잘못된것으로 생각된다... 참고로 해당 포트폴리오의 종목은 필자의 실제 투자 포트폴리오이다.