Kalman Filter
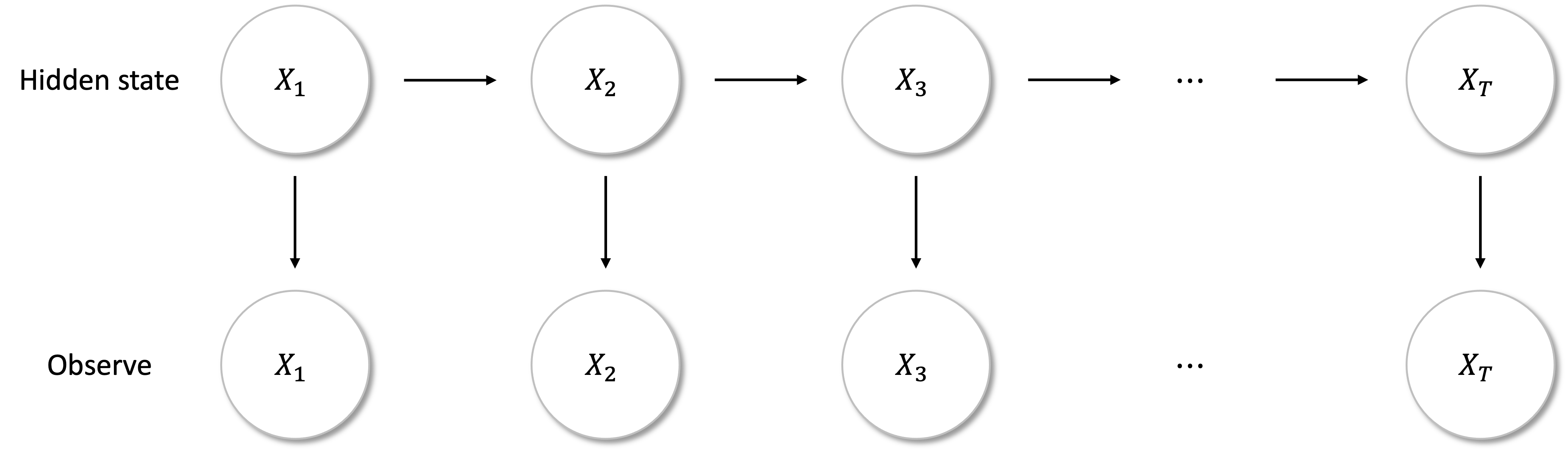
칼만필터는 확률모델을 기반으로 시계열과 같은 순차적 데이터에 대한 동적 선형 모델로 새로운 데이터를 시게열의 현재값 추정에 반영한다. 구체적으로는 시계열에 따른 관측치 Z에 대해 은닉변수 X의 사후 분포를 추정하는 베이지안 접근법을 따른다.
알고리즘의 기본 아이디어는 관측치로부터 현재 상태를 추정하고, noise가 섞인 관측치를 기반으로 더 확실한 추정치에 높은 가중을 두어 추정치를 업데이트하는 방식이다. 그리고, 칼만필터는 아래와 같은 가정을 따른다.
모델링하는 시스템은 선형방식으로 작동한다.
은닉 상태 프로세스는 마르코프 체인이으로 현시점의 은닉상태는 바로 전시점의 은닉상태에만 의존한다.
가중치 측정은 고정공분산의 가우시안, 비상관 잡음에 제약된다.
결과적으로 칼만필터는 은닉변수가 연속변수이고, 은닉과 관측변수 모두가 정규분포 𝑵(μ,𝜎)를 갖는다는 점을 제외하고는 은닉마르코프모델(HMM, Hidden Markov Model)과 유사하다.
파이썬에서 사용가능한 칼만필터 패키지의 파라미터는 다음과 같다.
- Initial state: 초기 은닉상태는 정규분포를 따르고 다음과 같은 initial_state_mean, initial_state_covariance 𝑥0 ~ 𝑵(μ0,∑0)를 가진다.
- Hidden state: 은닉상태 𝑥t+1은 전이행렬 transition_matrix 𝐴, 전이편향 transition_offset 𝑏 그리고 추가된 가우시안 noise가 전이공분산 transition_covariance 𝑄를 갖는 𝑥t+1= 𝐴t𝑥t + 𝑏t + ε1t+1, ε1t ~ 𝑵(0,𝑄)의 선형변환이다.
- Observe data: 관측치 𝑧t는 관측행렬 obaservation_matrix 𝐶, 관측편향 observation_offset 𝑑 그리고 추가된 가우시간 noise가 관측공분산 observation_covariance 𝑅을 갖는 𝑧t= 𝐶t𝑥t + 𝑑t + ε2t, ε2t ~ 𝑵(0,𝑅)의 선형변환이다.
이러한 칼만필터의 장점은 금융데이터와 같이 이분산성을 가지는 non-parametric 데이터를 유연하게 적은 한다는 것인데, 종종 금융데이터가 선형성과 가우시안 noise 가정을 위배해 확장형 칼만필터 또는 무향칼만필터를 적용하기도 한다.
이렇게 까다로운 모형 적합에도 불구하고 칼만필터는 새로운 관측치를 기반으로 더 최근의 관측치에 가중치를 더 크게 주는 방식으로 매 타임스텝마다 추정치를 적응하기 때문에, 주가추정에 자주 활용되는 이동평균 기법 대비 더 정확한 추정이 가능하다.
Kalman Filter for Python
다음으로는 칼만필터 패키지인 pykalman을 활용해 마이크로소프트의 주가의 white noise를 줄이고, 예측하는 작업을 시행해보자. 매우 간단한 연습으로 세부적인 연습은 다음에 한번 더 시행하겠다. 우선, yahoo finance api를 통해서 마이크로소프트의 2021년 8월 1일부터 2022년 8월 16일까지의 데이터를 가져온다.
from datetime import datetime
import pandas as pd
import yfinance as yf
from pykalman import KalmanFilter
ticker = yf.Ticker("MSFT")
today = datetime.today()
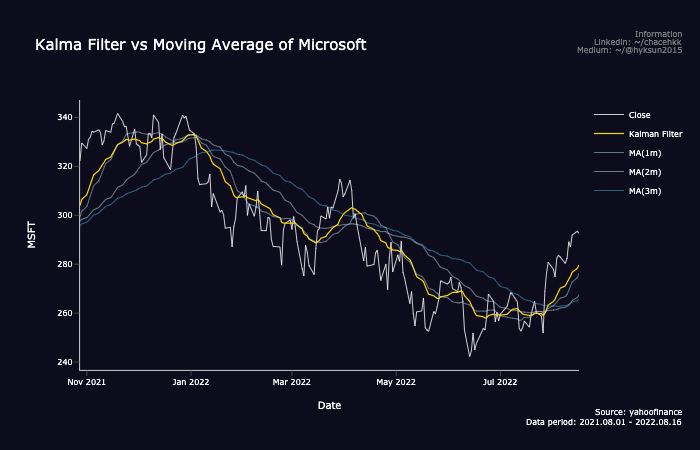
df = ticker.history(start='2021-08-01',end=today)그리곤, 칼만필터의 초기값을 설정해야 하는데 우리는 간단하게 transition matrix와 observe matrix는 단위행렬로 설정하고, initial mean은 1, covariance는 0으로 설정해, 칼만필터 패키지로 필터링 하여 이를 다시 원래 데이터셋에 맵팽하여 이동평균선과 비교해보았다.
#initial state
kf = KalmanFilter(transition_matrices = [1], #A
observation_matrices = [1], #C
initial_state_mean = 0,
initial_state_covariance = 1,
observation_covariance = 1,
transition_covariance = 0.01)
#estimate observe data
filtered_state_mean, filtered_state_covariance = kf.filter(df['Close'])
#mapping to df
df['Kalman Filter'] = filtered_state_mean
#moving average caculating
for months in [1,2,3]:
df[f'MA ({months}m)'] = (df['Close'].rolling(window=months * 21).mean())
df = df.dropna()결과적으로 다음과 같은 plot을 그릴 수 있는데, 칼만필터가 원래 시계열 자료의 white noise를 많이 줄였고, 1개월 이동평균선과 유사한 모습을 보였다. 하지만, 2022년 3월과 같이 급등한다던가 2022년 1월과 같이 급락하는 등 주가 변동성이 커졌을때는, 이동평균선보다 더 민감하게 반응한다는 것을 알 수 있었다.