Non-Parametrix VaR
지난 포스팅에서 리스크의 분포가 표준정규분포를 따른다는 가정하에 VaR을 구했었다. 하지만 이는 현실세계에 적용 불가능한 부분이 있어, 이번 포스팅에서는 Monte Carlo Simulation을 통해서 분포를 만든 후, quantile 값으로 신뢰구간을 추정할 것이다.
Monte Carlo Simulation이란, 간단하게 설명하자면 난수를 부여해서 분포를 만드는 것이다. 우리는 현실세계에 모든 데이터를 수집할 수 없고, 그 분포를 추정하는데 어려움이 있다. 그렇기 때문에 여러번 샘플링을 하여, 직접 분포를 만드는 것이다. 그리고, 이 분포에서 분위수값을 추정하게 되는데, 이는 사실 나도 이해하기 좀 어려운 부분이다...
어쨌든, 우리의 목적은 non-parametric VaR을 추정하는 것이므로, 분위수 값을 구하기 위해 누적분포 함수로부터 VaR을 아주 많이 얻어 99%, 95%, 90% 신뢰구간에 해당하는 VaR을 얻게 되는 것이다.
Monte Carlo Simulation이란, 간단하게 설명하자면 난수를 부여해서 분포를 만드는 것이다. 우리는 현실세계에 모든 데이터를 수집할 수 없고, 그 분포를 추정하는데 어려움이 있다. 그렇기 때문에 여러번 샘플링을 하여, 직접 분포를 만드는 것이다. 그리고, 이 분포에서 분위수값을 추정하게 되는데, 이는 사실 나도 이해하기 좀 어려운 부분이다...
어쨌든, 우리의 목적은 non-parametric VaR을 추정하는 것이므로, 분위수 값을 구하기 위해 누적분포 함수로부터 VaR을 아주 많이 얻어 99%, 95%, 90% 신뢰구간에 해당하는 VaR을 얻게 되는 것이다.
Non-parametric VaR for Python
파이썬으로 실습은 지난번과 비슷하다. 공분산 행렬을 통해서 포트폴리오의 분산을 추정하는 부분은 지난번과 동일하다. 하지만, monte carlo simulation을 하기 위해 표준정규분포 내에서 반복 횟수만큼의 난수를 생성해주어야 한다.
tickers = ['AAPL','MSFT','BRK-B','DIS']
w = np.array([0.24,0.3,0.15,0.3]) #포트폴리오 가중치
df = yf.download(tickers,start='2021-01-01',end = '2022-08-16')[['Close']]
df = np.log(df)
df = df.pct_change()
df = df.dropna()
df.head()N = 20
trading_days = len(df.index)
mean_p = df.mean().to_numpy().dot(w) #portfolio expected return
cov = df.cov() #포트폴리오 공분산 계산
std = np.sqrt(w.T.dot(cov).dot(w)) #포트폴리오 표준편차
iterations = 50000 #반복횟수def MC_VaR(expected_return, standard_deviation, T, iterations):
values = 1- np.exp((expected_return - 0.5 * standard_deviation ** 2) * T + standard_deviation * np.sqrt(T) * np.random.standard_normal(iterations))
return values
var = MC_VaR(expected_return = mean_p, standard_deviation=std, T = N/trading_days, iterations = iterations)
var그 결과 99% 신뢰구간에서 VaR은 0.123%, 95%에서는 0.087%, 90%에서는 0.068%의 확률로 손실발생이 가능하다.
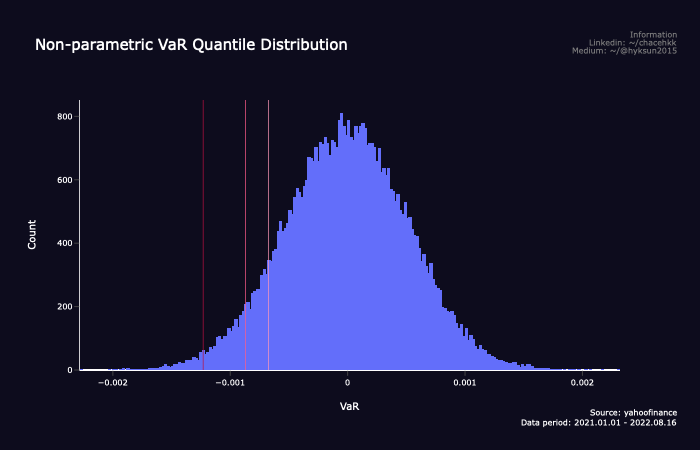
그리고 이를 parametric과 non-parametric에서 각각 비교하면 아래와 같다. 보다싶이 매우 유사한 수준의 VaR이 나왔는데 non-parametric이 0.001%p높아 아주 미세하게 보수적으로 접근한것으로 보인다.
Code: https://github.com/hyeokkukim/python-for-finance/blob/main/Value_at_Risk(VaR).ipynb
