https://www.acmicpc.net/problem/1074
분류
분할 정복(divide_and_conquer), 재귀(recursion)
문제 설명
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.
N > 1인 경우, 배열을 크기가 2N-1 × 2N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 22 × 22 크기의 배열을 방문한 순서이다.
N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음은 N=3일 때의 예이다.
입력
첫째 줄에 정수 N, r, c가 주어진다.
출력
r행 c열을 몇 번째로 방문했는지 출력한다.
풀이과정
문제 설명에서 재귀라는 힌트를 주어서 재귀를 사용해서 풀어야 한다는 것을 파악했다. 하지만 분할 정복이라는 것을 생각하지 못 해 문제를 푸는 시간이 정말 오래걸렸다.
-
문제의 모든 규칙은 Z에 모양대로 1, 2, 3, 4 순서로 움직이기 때문에 이와 맞게 4등분으로 분할해야한다. 그래서 먼저 가로, 세로의 절반 길이 값을(half) 구해준다. -> 2N의 반
-
그리고 분할된 사분면 마다 첫 번째 값는 half의 제곱의 배수이다.
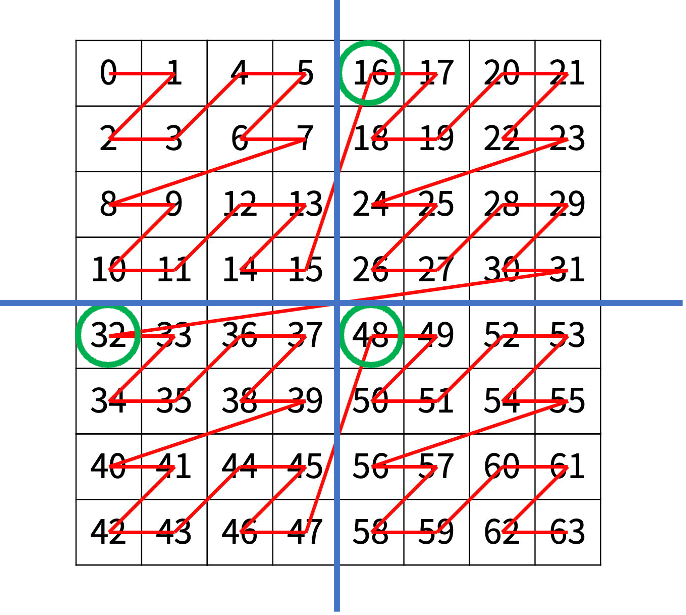
위와 같이 N이 3일 때, half는 4(23 / 2) 이고 각 사분면의 첫 번째 값은 42의 배수이다. (16, 32, 48)
-
그래서 가로, 세로마다 위에서 구한 half를 넘는지 아닌지 판별하여 N은 1씩, 가로, 세로 길이는 half 만큼 줄여가며, 결과 값(result)에는 사분면의 첫 번째 값을 더해준다.
-
N이 1이 되었을 때, 가장 작은 Z 형태 (0, 1, 2, 3)에 이제까지 더한 결과 값(result)를 더하면 된다.
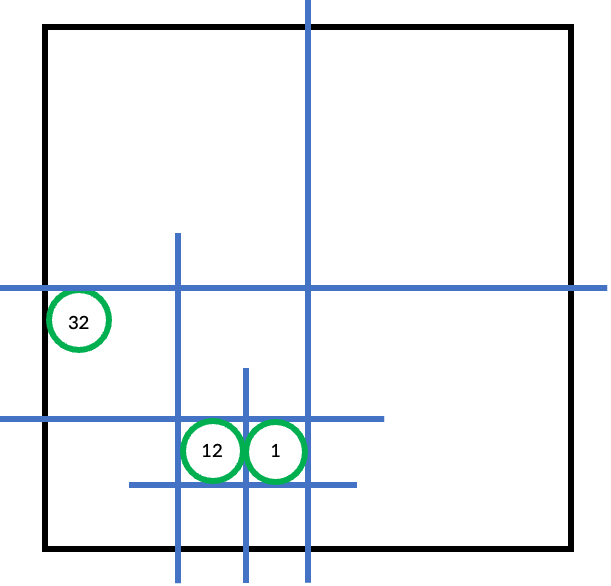
예를 들어 N이 3일 때 r = 6, c = 3 인 값을 찾으려 한다 해보자.
half는 4(23 / 2)이고 (6, 3)은 3사분면에 있기 때문에 3사분면에 첫 번째 값인 32를 더해준다.
그리고 분할된 사분면(N = 2)에서 또 4분면에 속하기 때문에 12를 더해준다.
N = 1이 되었으므로 Z 형태의 2번 째 값인 1을 더해준다.
그럼 32 + 12 + 1 = 45 라는 정답을 금방 구할 수 있다!
코드
let input = readLine()!.split(separator: " ").map{ Int(String($0))! }
let N = input[0], R = input[1], C = input[2]
let Z = [[0, 1], [2, 3]]
func recursion(n: Int, r: Int, c: Int, result: Double) -> Int {
if n == 1 {
return Z[r][c] + Int(result)
}
let half = Int(pow(2.0, Double(n)) / 2)
if r < half && c < half { // 1사분면
return recursion(n: n - 1, r: r, c: c, result: result)
} else if r < half && c >= half { // 2사분면
return recursion(n: n - 1, r: r, c: c - half, result: result + pow(Double(half), 2.0))
} else if r >= half && c < half { // 3사분면
return recursion(n: n - 1, r: r - half, c: c, result: result + pow(Double(half), 2.0) * 2)
} else { // 4사분면
return recursion(n: n - 1, r: r - half, c: c - half, result: result + pow(Double(half), 2.0) * 3)
}
}
print(recursion(n: N, r: R, c: C, result: 0))
