유클리드 호제법을 활용한 최대공약수와 최소공배수 구하는 방법에 대해서 알아보자!
최대공약수 & 최소공배수
최대공약수(GCD, Greateast Common Division)와 최소공배수(LCM, Least Common Multiple)
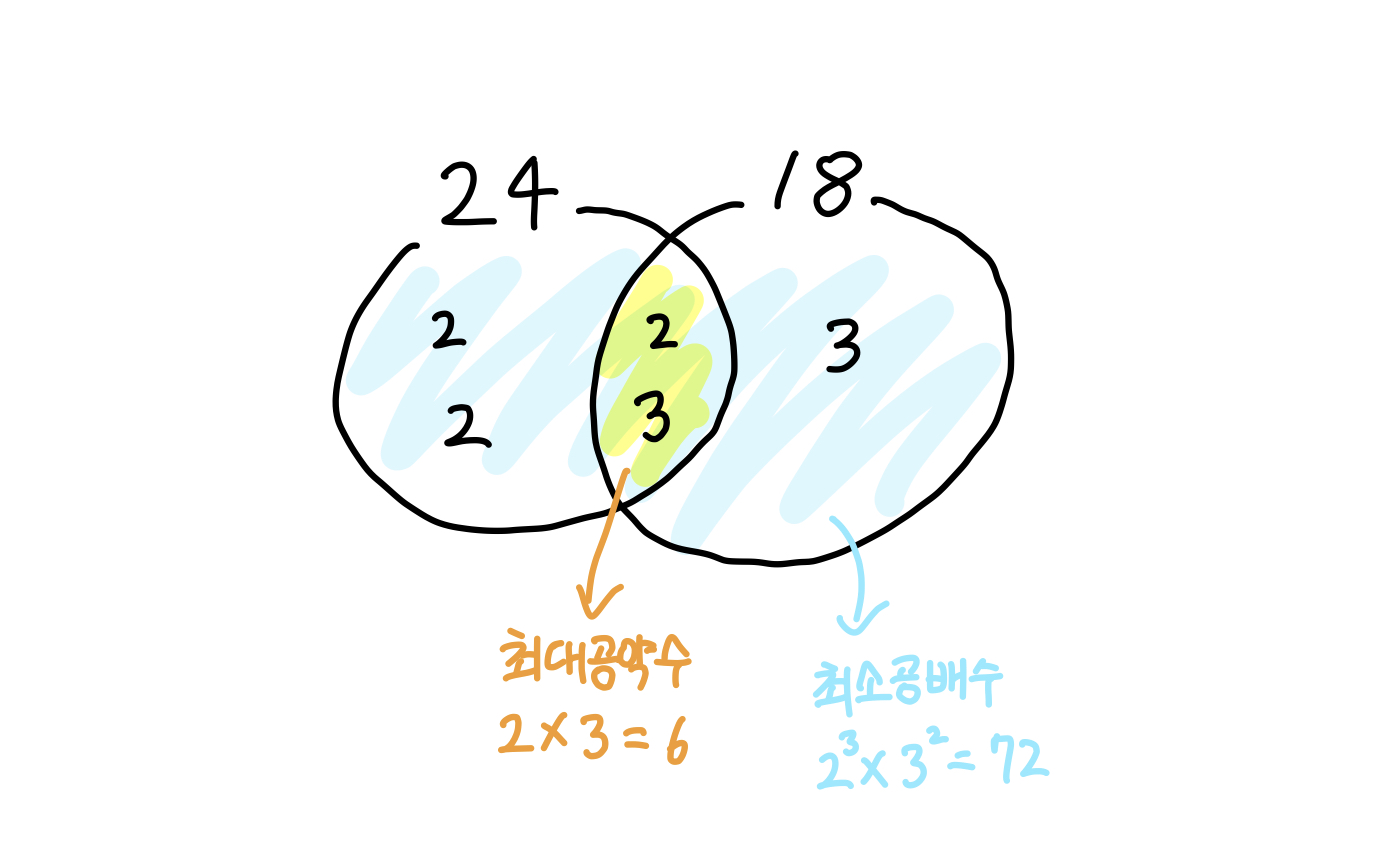
두 수 A,B의 최대공약수를 G, 최소공배수를 L이라고 하면, " AB=LG " 가 성립한다.
유클리드 호제법 이란??
유클리드 호제법(Euclidean algorithm) 또는 유클리드 알고리즘은 2개의 자연수의 최대공약수를 구하는 알고리즘의 하나이다.
호제법이란 말은 두 수가 서로(互) 상대방 수를 나누어(除)서 결국 원하는 수를 얻는 알고리즘을 나타낸다.
(a>b 일때) 2개의 자연수 a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면,
a와 b의 최대공약수는 b와 r의 최대공약수와 같다.
이 성질에 따라, b를 r로 나눈 나머지 r'를 구하고, 다시 r을 r'로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수이다.
💡 요약) a > b일때, a%b = r이며, a와 b의 최대공약수를 gcd(a,b)라고 하면,
gcd(a,b) = gcd(b,r)이 성립한다.
예시)
78696과 19332의 최대공약수를 구하면,
78696 = 19332×4 + 1368
19332 = 1368×14 + 180
1368 = 180×7 + 108
180 = 108×1 + 72
108 = 72×1 + 36
72 = 36×2 + 0따라서, 최대공약수는 36이다.
위의 최대공약수와 최소공배수의 관계에서 AB=LG 이므로,
최소공배수 L은 두수 A,B의 곱 / 최대공약수 이므로
💡 최소공배수 lcm = (a*b) / gcd(a,b) 가 된다.
