다익스트라 알고리즘
그래프에서 여러 개의 노드가 있을 때, 특정한 한 정점(=노드)에서 출발하여 다른 모든 정점으로 가는 최단 경로를 구하는 알고리즘
구현방법
방법 1
- 출발 노드를 설정
- 최단 거리 테이블 초기화
- 방문하지 않은 노드 중에서 최단 거리(가중치)가 가장 짧은 노드 선택
해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신 - 위 과정에서 3, 4번 반복
private data class Node(val nodeNum : Int, val weight: Int)
fun solution () {
val map = Array(N+1){Vector<Node>()}
// 그래프가 들어 있는 배열
val route =IntArray(N+1){MAX}
// 최소 거리를 저장할 배열
val visited = BooleanArray(N+1){false}
val queue = LinkedList<Node>()
for(i in 1..M){
val br = readLine().split(" ").map{it.toInt()}
map[br[0]].add(Node(br[1], br[2]))
}
route[start]=0
if(map[start].size>0)
queue.add(Node(start,0))
while(queue.isNotEmpty()){
val cur = queue.poll()
if(visited[cur.nodeNum]) continue
visited[cur.nodeNum] = true
for(vertex in map[cur.nodeNum]){
val cost = route[cur.nodeNum] + vertex.weight
if( !visited[vertex.nodeNum] && cost < route[vertex.nodeNum] ){
route[vertex.nodeNum] = cost
queue.add(Node(vertex.nodeNum,cost))
}
}
}
}방법 1도 충분히 좋은 알고리즘이지만 우선순위 큐를 사용하면 조금 더 시간을 단축할 수 있다
방법2
우선순위 큐를 이용해서 구현하였을 때, 동작방식은 인접한 간선들을 모두 Queue에 집어 넣은 후, 최소힙을 구하는 연산을 통해서 최소비용이 드는 정점들부터 처리하는 방식이다
우선순위 큐에 관한 포스팅은 여기에 정리해 놓았다
우선순위 큐를 사용해 가중치 기중으로 오름차순 한다는 것이 포인트
위의 코드와 달라진 점은
queue 를 PriorityQueue 로 변경하고
가중치 비교를 위해 Node 클래스에서 Comparable을 오버라이드 해주었다는 것
이제 탐색할 때 연결된 노드 중에서 거리가 가장 짧은 노드부터 탐색하게 될 것이다
private data class Node(val nodeNum : Int, val weight: Int) : Comparable<Node>{
override fun compareTo(other: Node): Int {
return weight - other.weight
}
}
//Comparable 오버라이드
fun solution () {
val map = Array(N+1){Vector<Node>()}
// 그래프가 들어 있는 배열
val route =IntArray(N+1){MAX}
// 최소 거리를 저장할 배열
val visited = BooleanArray(N+1){false}
val queue : PriorityQueue<Node> = PriorityQueue();
// 우선순위 큐로 교체
for(i in 1..M){
val br = readLine().split(" ").map{it.toInt()}
map[br[0]].add(Node(br[1], br[2]))
}
route[start]=0
if(map[start].size>0)
queue.add(Node(start,0))
while(queue.isNotEmpty()){
val cur = queue.poll()
if(visited[cur.nodeNum]) continue
visited[cur.nodeNum] = true
for(vertex in map[cur.nodeNum]){
val cost = route[cur.nodeNum] + vertex.weight
if( !visited[vertex.nodeNum] && cost < route[vertex.nodeNum] ){
route[vertex.nodeNum] = cost
queue.add(Node(vertex.nodeNum,cost))
}
}
}
}
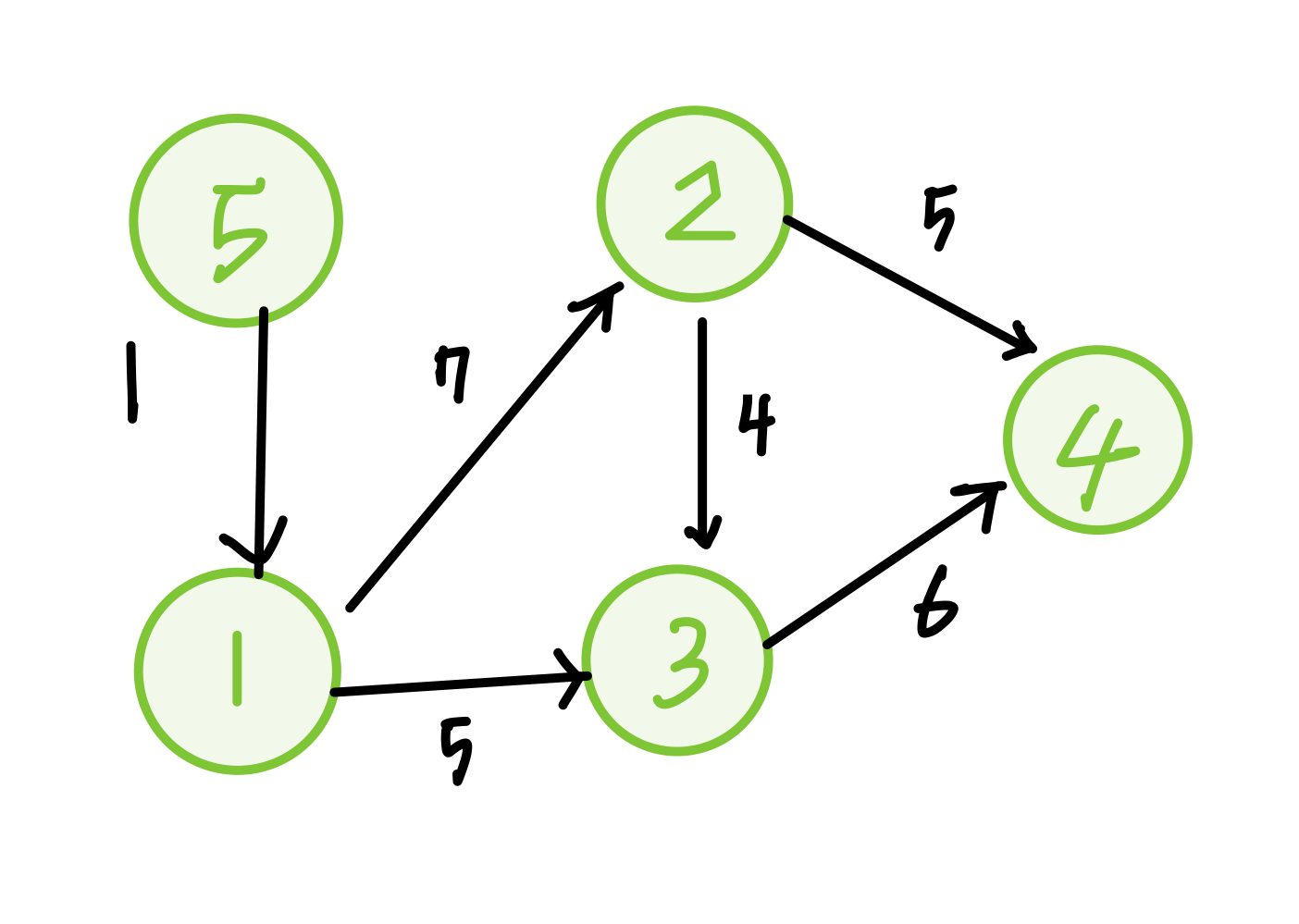
가정 : 출발 노드는 1 , 인접 노드 리스트으 nodeNum 순서는 오름차순이다
이 문제를 방법 1과 방법2 각각 해결해보면
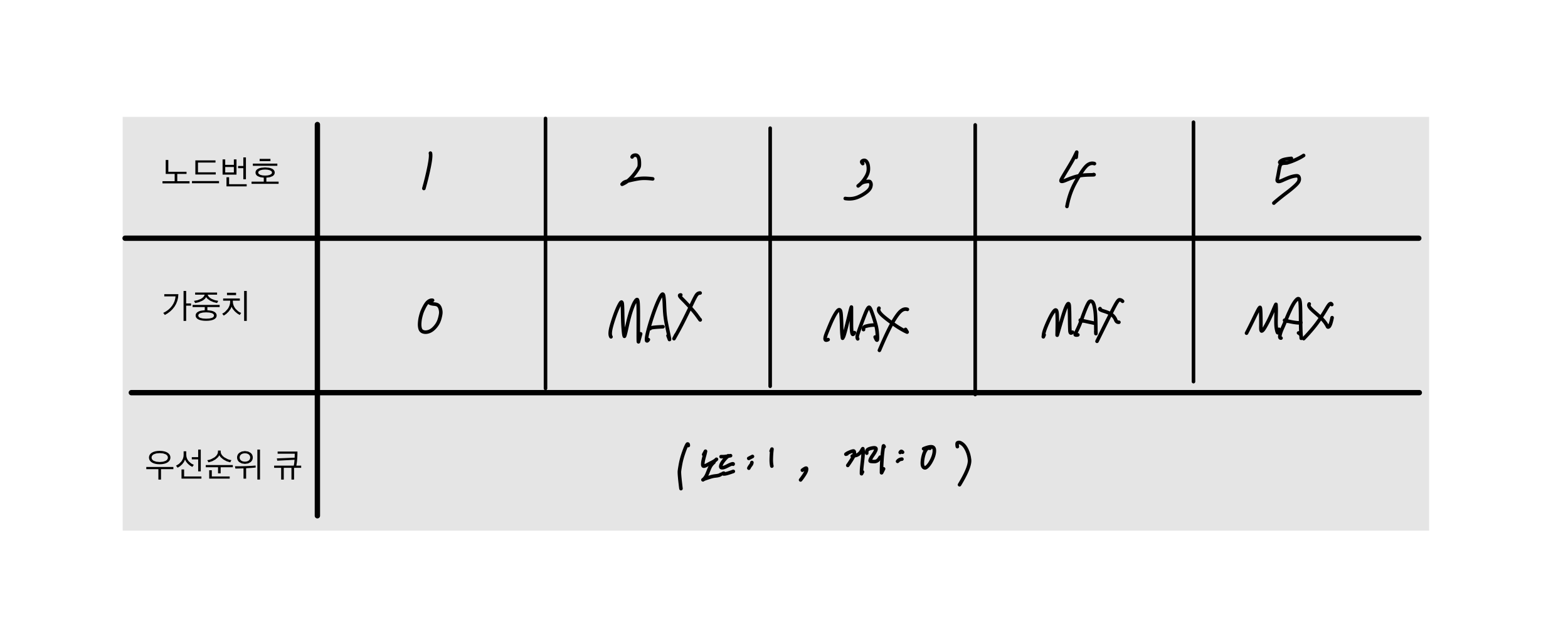
처음 시작노드인 1 을 넣는 것은 동일하다
방법1로 해결한 과정

- 큐에 차례대로 2,3 노드를 넣어준다
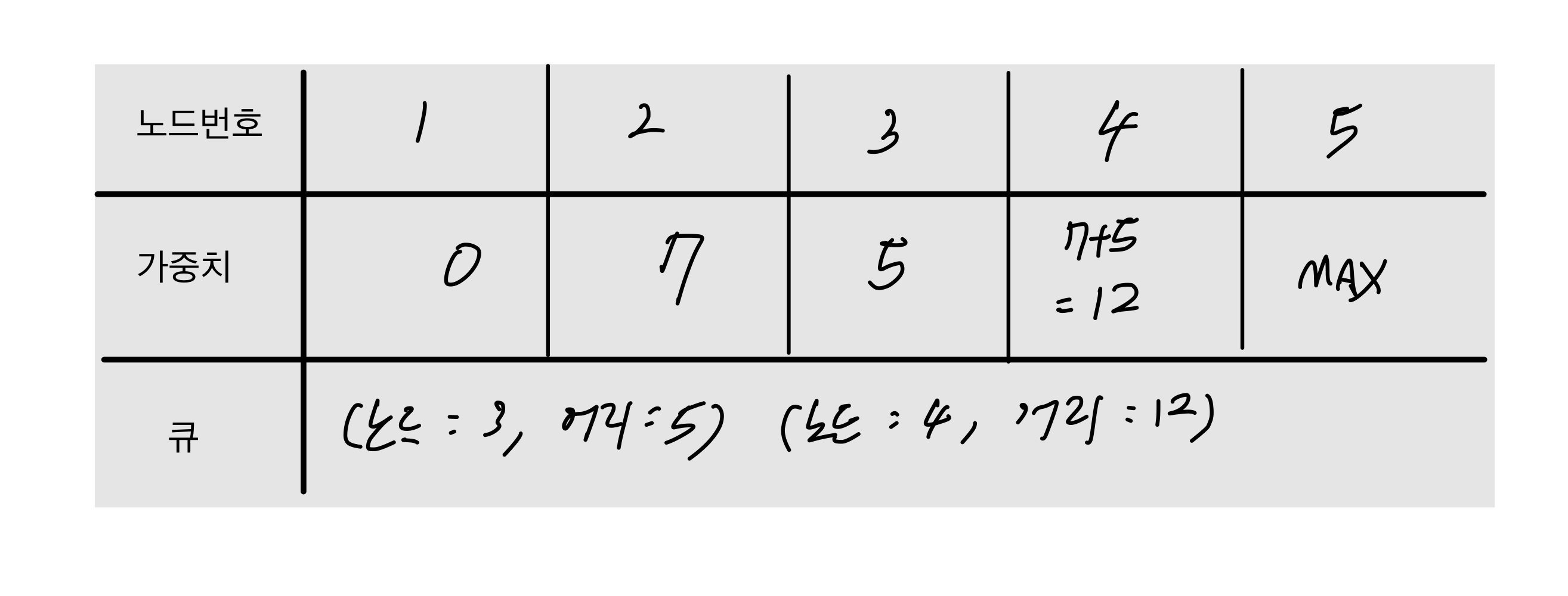
- 큐에서 2번 노드르 꺼내고 인접 노드인 4번 노드를 넣어준다.
거리는 1->2->4 = 7+5 이고 MAX 값보다 작기 때문에 갱신해준다
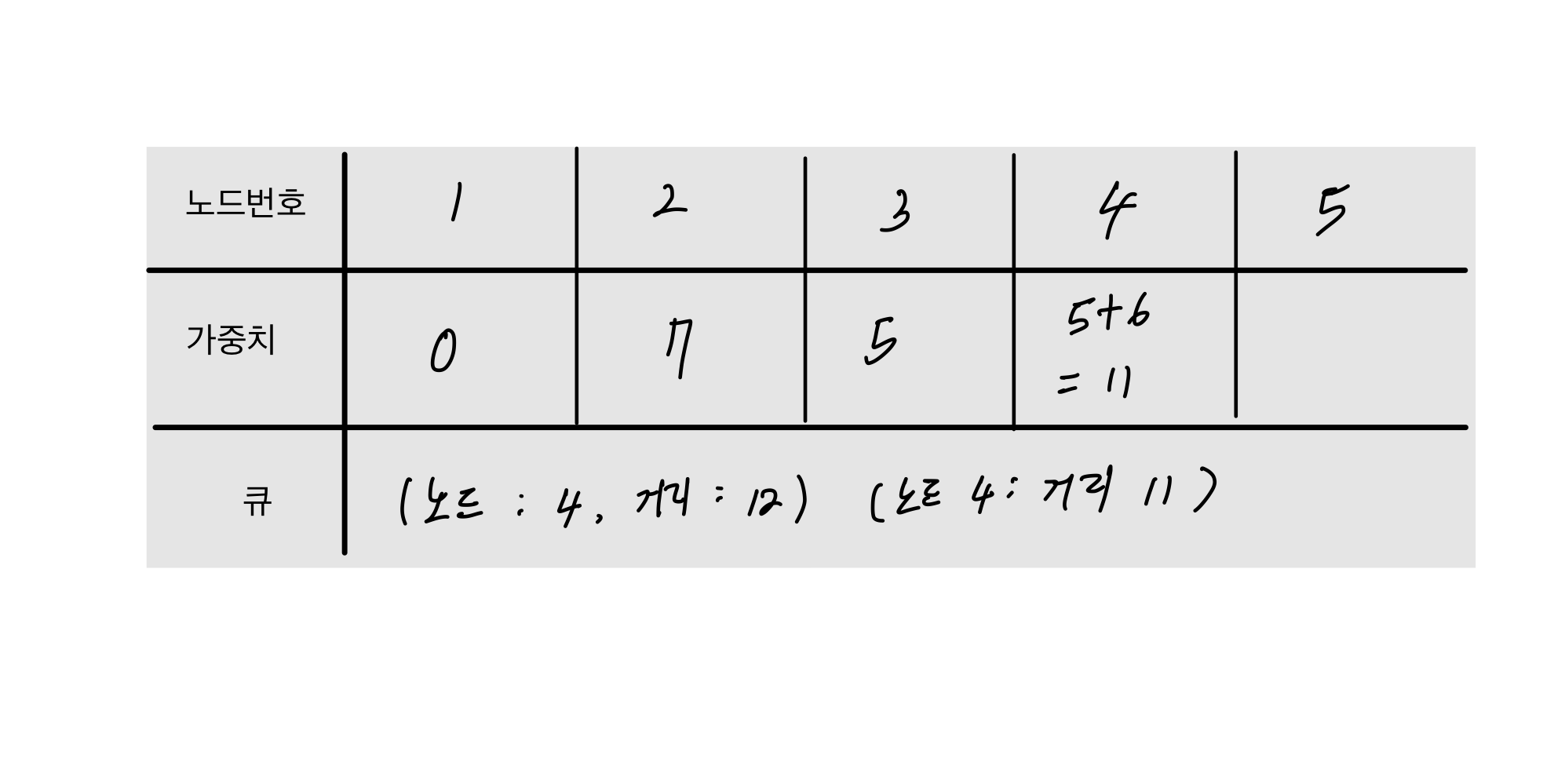
3. 큐에서 3번 노드르 꺼내고 4번노드의 기존의 값 12 보다 1->3->4 = 5+6 = 11 로 작기 때문에 갱신해준다.
-
큐에서 4번 노드를 꺼낸다. (노드 4: 거리 12) 방문 처리를 해주고
현재의 값 =12 와 기존 노드 4의 값 : 11 을 비교했을 때 더 크기 때문에 갱신은 하지 않는다. -
큐에서 나머지 (노드 4 : 거리 11) 을 꺼내고 이미 방문한 노드이기에 continue
-
큐가 비었기 때문에 종료
방법2로 해결한 과정
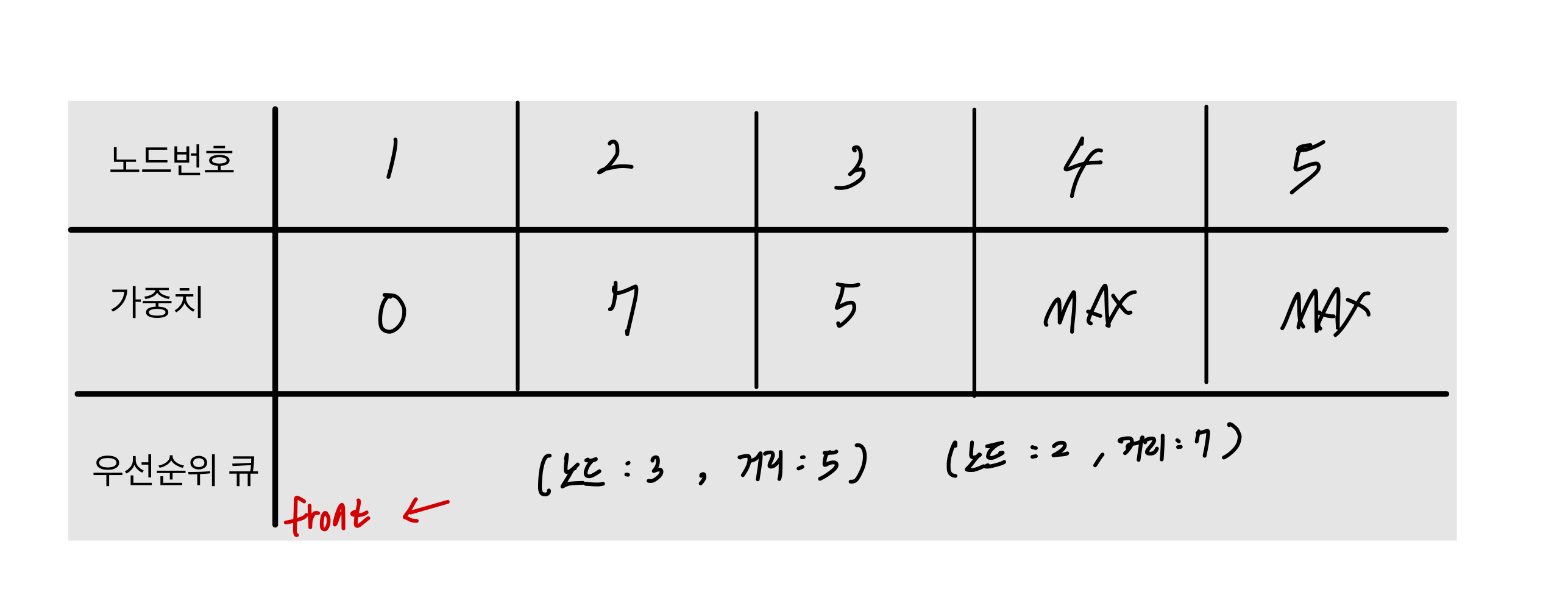
- 거리가 가까운 노드 부터 집어 넣는다 . 방법1과 달리 3번이 먼저 들어가게 된다.
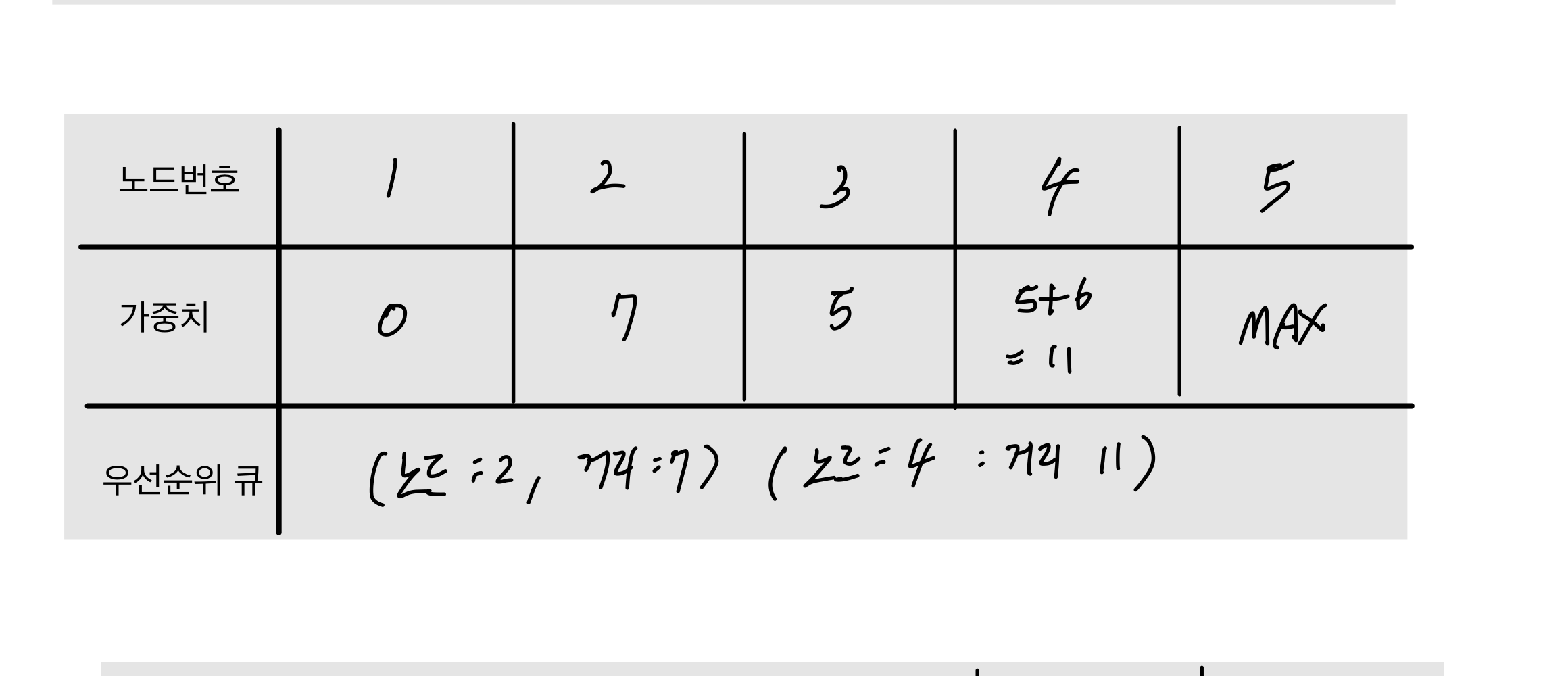
- 노드 3의 인접 노드 4를 넣고 1->3->4 = 5+6 으로 Max 보다 작기 때문에 갱신해준다
-
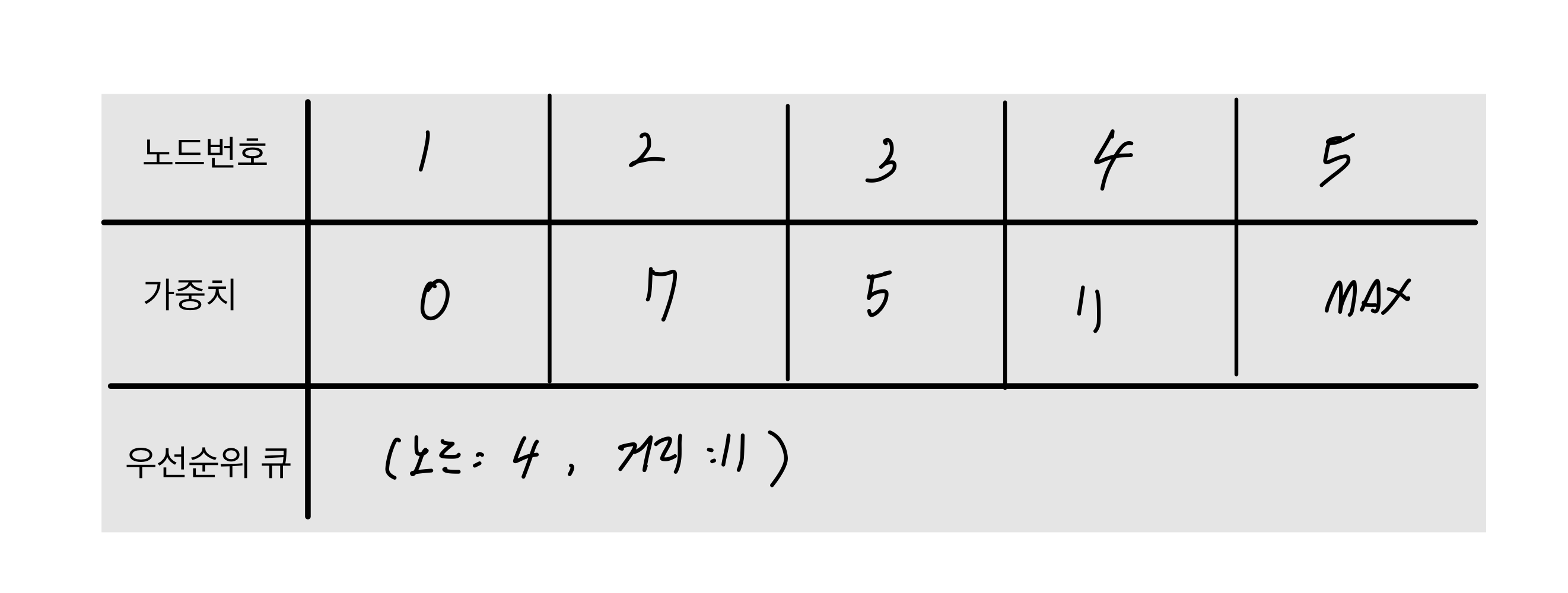
노드2의 인접노드인 4를 넣으려고 하지만 1->2->4 = 7+5 =12 로 기존의 값 11 보다 크기 때문에 갱신하지 않고 넣지 못한다.
-
큐에서 나머지 (노드 4 : 거리 11) 을 꺼내고 이미 방문한 노드이기에 continue
-
종료
과정을 한번 줄인 것으로 큰 차이가 없어 보일 수 있지만 노드의 수가 많아지게 되면 성능에 향상에 도움이 됨이 분명하다
우선순위 큐 사용을 권장하는 이유이다.
시간복잡도
시간 복잡도는 O(ElogV) 이다. (E: 간선의 개수, V: 노드의 개수)
우선 우선 순위 큐는 Heap 구조로 되어있기 때문에 O(logN) 이다.
다익스트라 알고리즘을 전체적으로 보면 각 노드 별로 인접한 노드의 최단 거리를 확인하는 작업을 반복한다. 즉, 간선의 개수 E 개 만큼 우선 순위 큐에 넣었다가 모두 빼는 과정을 한다고 생각할 수 있다.
결국 O(ElogE) 의 복잡도를 가지게 된다.
모든 노드가 서로 연결되었을 때 최대 V^2 개의 간선이 생길 수 있기 때문에
E 는 항상 V^2 보다 작거나 같다.
O(ElogE) <= O(ElogV^2)
O(ElogV^2) -> O(2ElogV) -> O(ElogV)
결국 O(ElogE) <= O(ElogV) 가 되고,
시간 복잡도를 O(ElogV) 라고 할 수 있다.
참고
https://m.blog.naver.com/ndb796/221234424646
https://yabmoons.tistory.com/364

