Dynamic Programing (동적계획법) with Kotlin

한 번 계산한 문제는 다시 계산하지 않도록 하는 알고리즘

다이나믹 프로그래밍은 큰 문제를 작게 나누고, 같은 문제라면 한 번씩만 풀어 문제를 효율적으로 해결하는 알고리즘 기법이다.

분할 정복 방식과 비슷한데, 차이점은 다이나믹 프포그래밍에서는 작은 문제들이 반복되지만 분할정복은 그렇지 않다는 것이다.

동적 계획법 특징

DP는 두가지 조건을 만족할 때 사용할 수 있다.

이러한 조건 때문에 작은 문제를 푼 값들을 저장하고 큰 문제를 풀 때 이 값을 사용하여 연산 시간을 줄여나가는 알고리즘이다.

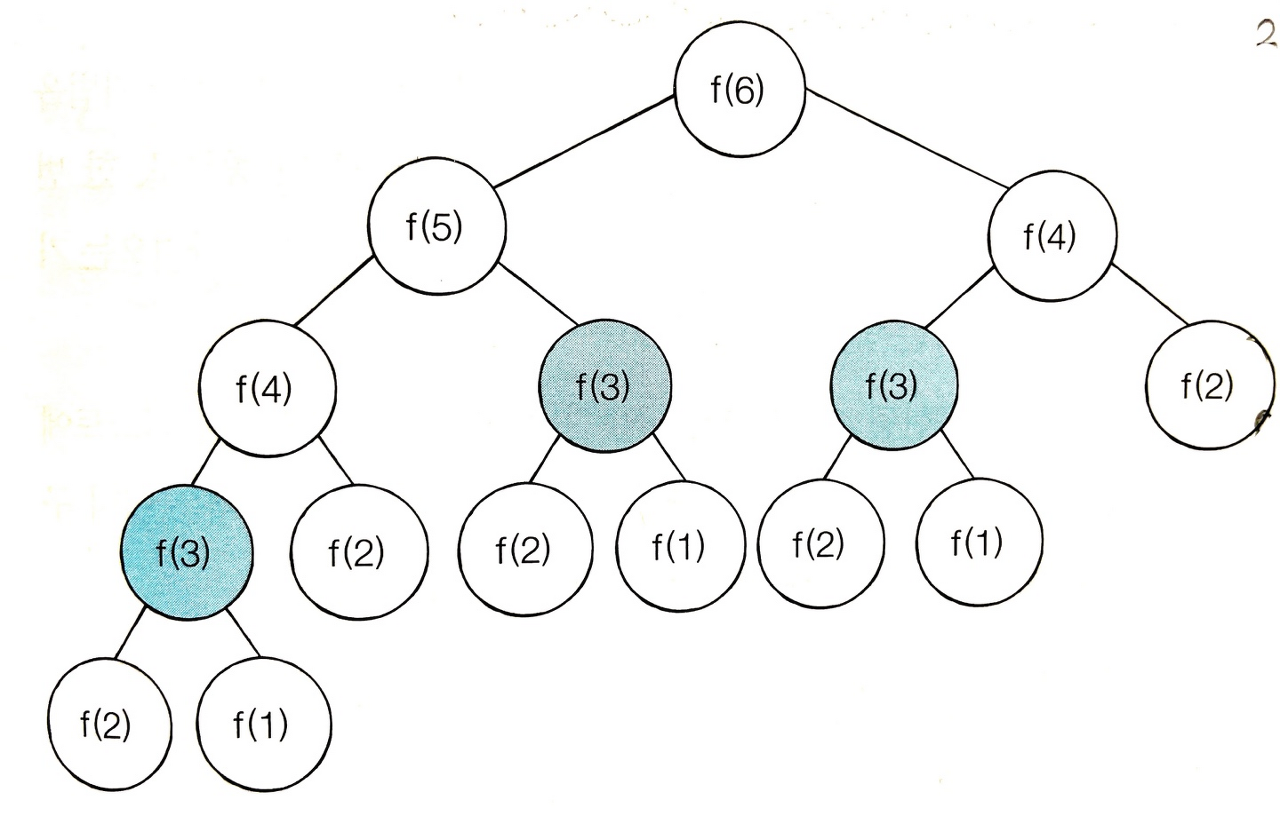
출처 : 이것이 코딩 테스트다 (나동빈, 한빛미디어)

예를 들면 큰 문제인 f(6)을 해결하기 위해서는 3번의 f(3)연산이 필요하다.
하지만 같은 동작을 3번 반복하는 것은 효율적이지 못하기 때문에, 한번 수행한 결과값을 저장하고, 다른 곳에서는 이 결과값만 가져다 쓰는 것이다. 메모리는 조금 더 쓰이겠지만 시간적으로는 충분히 효율적이다.

이때, 작은 부분 문제가 반복될 때 저장된 결과값을 활용하는 방식을 메모이제이션(memoization) 또는 캐싱(caching) 이라고 한다.

피보나치

fun fibonachi(n : Int) : Int{
    return if(n<=1) n;
    else{
        fibonachi(n-1)+fibonachi(n-2)
    }
}

피보나치 수열을 재귀를 통해 구하는 방식을 살펴보면 큰 문제 Fn을 구하기 위해 작은 문제 F(n-1) 과 F(n-2) 가 실행되고 이 것들은 또 F(n-2) F(n-3) 의 큰 문제가 된다. 또한 이 과정에서 F(n-2) F(n-3)가 2번 씩 겹친다.
Overlaping SubProblem 의 상황이 발생한 것이다.

이 코드의 시간 복잡도는 재귀 방식으로 O(2^n)이 된다.

피보나치 수열도 DP를 통해 최적화 할 수 있다.

다이내믹 프로그래밍 구현

구현 방식에는 2가지가 있다.

Top Down

1. 문제를 작은 문제로 나눈다
2. 작은 문제를 해결한다
3. 풀이한 작은 문제의 결과 값을 이용해 큰 문제를 해결한다

위에서 설명한 피보나치 수열을 Top Down 형식으로 해결해보자.

val memo = Array<Int>(1000) { 0 }

fun fibonachi(n : Int) : Int{
    return if(n<=1) n;
    else{
        memo[n] = fibonachi(n-1)+fibonachi(n-2)
        return memo[n]
    }
}

이 코드의 시간복잡도는 O(N)이다.
핵심은
memo[n] = fibonachi(n-1)+fibonachi(n-2)

정답을 구하면 메모리에 저장하는 메모리제이션을 활용한 것이다.

Bottom up

1. 크기가 작은 문제부터 해결한다
2. 크게 만들어 나가면서 풀이한다
3. 이 방식을 반복하며 원하는 큰 문제를 해결한다

fun fibonachi(n : Int) : Int{
    memo[0]=0;
    memo[1]=1;
    memo[2]=1;
    for (i in 2..n){
        memo[i]=memo[i-1]+memo[i-2];
    }
    return memo[n]
}

이 코드도 마찬가지로 시간복잡도는 O(N)이다.

상황에 따라 적합한 방식을 골라 해결하면 된다.