해당 논문은 Inception 모델을 설계하며 효율적인 그리고 효과적인 확장과 모델 아키텍처가 무엇인지에 대해 생각한다.
"Here we are exploring ways to scale up networks in ways that aim at utilizing the added computation as efficiently as possible by suitably factorized convolutions and aggressive regularization."
논문은 그중에서 Convolution Layer를 factorize하여 computational 성능을 개선하는 방법을 집중하여 다룬다.
논문에선 Inception 모델을 사용해 설명하였지만 논문에서 제시한 아이디어를 인사이트로 활용하여 다른 모델의 설계에도 유용한 활용이 가능할 것이다.
General Design Principles
해당 논문이 제시되기 전, 효율적인 모델 설계에 대한 방법은 여러번 다뤄졌다.
논문은 그 중 몇 가지 대표적인 방법을 제시한다.
1. Avoid representational bottlenecks, especially early in the network.
Deep Neural Network는 다음과 같이 acyclic graph로 표현이 가능합니다.
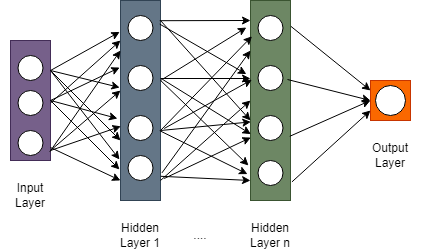
이때, graph의 화살표(간선)은 정보의 흐름을 나타냅니다.
각 layer에서 나온 정보들은 다음 layer로 흘러갑니다.
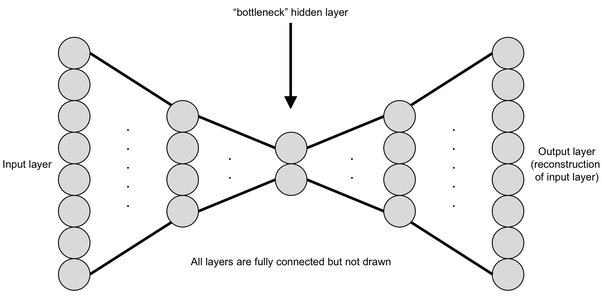
이때, 다음 layer에 소속되어 있는 node의 갯수가 이전 layer의 그것보다 작아지면 정보의 압축이 발생합니다.
그 과정에서 다음 layer가 받는 정보의 크기는 이전 layer의 그것보다 작습니다.
이러한 layer 구조를 Bottleneck(병목) 구조 라고 합니다.
적당한 비율로 node가 줄어들며 만들어지는 bottleneck 구조는 정보의 특징을 추출하는데에 큰 도움이 됩니다.
그러나 극단적으로 줄어드는 bottleneck은 추출한 특성의 양에 비해 너무나 많은 양의 정보를 손실하기에 "지양" 합니다.
2. Higher dimensional representations are easier to process locally with a network. Increasing the activations per tile in a convolutional network allows for more disentangled features.
고수준의 representation은 연산이 쉽습니다. layer (tile) 당 activation (앞서 말한 node와 동일)이 증가하는 것은 얽힌 특성들을 추출하는데 도움이 됩니다. 때문에 고수준의 특성을 추출할 때에는 activations per tile을 늘려주는 것이 도움이 됩니다.
3. Spatial aggregation can be done over lower dimensional embeddings without much or any loss in representational power.
공간적 특성은 저차원 임베딩에서 끝낼 수 있습니다. 이는 adjacent unit 간의 강한 상관관계가 차원축소에서 정보 손실을 더 줄여주기 때문입니다. 이러한 신호는 쉽게 압축 가능해야 한다는 점을 고려하면 차원 축소는 더 빠른 학습을 촉진합니다.
4. Optimal performance of the network can be reached by balancing the number of filters per stage and the depth of the network.
최적의 네트워크 성능은 각 stage 당 filter의 수가 깊어지고 많아질수록 달성할 수 있습니다.
단, 이때 width와 depth는 parallel하게 증가해야합니다.
위 4가지를 판단력 있게 사용함으로 모델의 성능을 개선시킬 수 있습니다.
Factorizing Convolutions with Large Filter Size
GoogLeNet Network의 대부분의 original gain들은 차원축소의 관대한 사용에서 시작되었습니다.
이는 계산적으로 효율적인 방식으로 Convolution을 Factorizing하는 특별한 경우로 볼 수 있습니다.
Vision Network에서는 인근 activation의 출력이 높은 상관관계를 가질 것으로 예상됩니다.
따라서 이들의 집계가 수행되기 이전에 activation이 줄어들 수 있으며 이로 인해 유사하게 표현되는 로컬 표현이 생성될 것으로 예상할 수 있습니다. 이때, 계산 비용을 줄이면 매개변수 수가 줄어듭니다.
이는 적절한 Factorization을 통해 더 많은 매개변수를 풀 수 있어 더 빠른 훈련이 가능하다는 것을 의미합니다.
또한 계산 및 메모리 절약을 사용하여 각 모델을 훈련하는 능력을 유지하면서 네트워크의 filter bank 크기를 늘릴 수 있습니다.
한마디로, 하나의 Convolution을 여러개의 작은 Convolution으로 쪼개라는 것 입니다.
Factorization into smaller Convolutions
앞서 말했듯, 하나의 Convolution을 여러개의 작은 Convolution으로 쪼갭니다.
예를들어, 5X5 크기의 Convolution 하나를 3X3 크기의 Convolution 2개로 나누는 것입니다.
이렇게 Convolution을 나눠도 인근 activation이 높은 상관관계를 가지기에 유사한 representation을 얻을 수 있음과 동시에 계산 비용도 줄어듭니다.
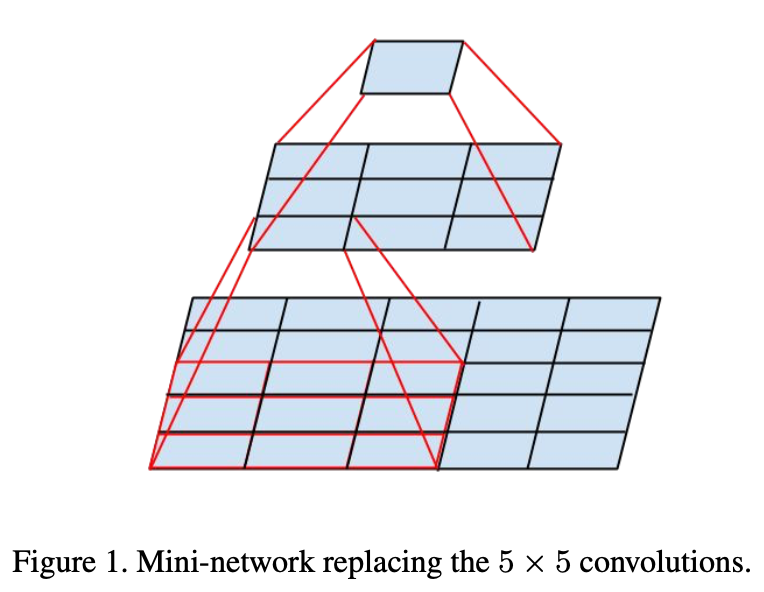
Factorized 된 Convolution은 이후 Dense Layer들과 연결됩니다.
이렇게 연결된 Convolution들은 정보 손실도 크지 않습니다.
Spatial Factorization into Asymmetric Convolutions
MxM 사이즈의 Convolution을 mxm 사이즈의 Convolution으로 Factorize 하는 것은 가능합니다.
그렇다면 MxM 사이즈를 1xM이나 Mx1로 Factorize 하는 것은 어떨까요?
이론상 가능합니다! 또한 Computational Cost도 n이 증가함에 따라 획기적으로 줄어듭니다.
그러나, 이것이 항상 통하는 것은 아니며 Medium grid sizes (On mxm feature maps, where m ranges 12 to 20)에서만 효과가 좋습니다. (early layer에서는 해당 방법에 유용하게 사용되지 않습니다.)
논문에 의하면 medium grid sizes의 level에서 7x1 -> 1x7 순서의 Convolution 구조가 좋은 성능을 보여주었습니다.

위 그림은 어떤 방식으로 Convolution Factorizing을 진행하는지에 대한 참고용 이미지입니다.
Utility of Auxiliary Classifiers
원래 방법으로는 lower layers의 useful gradients를 가져오는 것이 최적화 수렴에 도움이 되며 더욱 안정적인 학습이 가능하다고 알려져 있습니다.
그러나 이것들의 효과는 훈련 말미에서나 드러납니다.
또한 이러한 branch들이 저수준 특성을 키우는 것에 도움을 준다는 가정은 대부분 잘못되었습니다.
논문에서는 auxiliary classifier를 "regularizer"의 역할을 한다고 주장합니다.
즉, auxiliary branch는 성능 향상에 큰 도움이 되지 못합니다.
오히려 normalizer인 경우에 main branch의 성능이 크게 향상됩니다.
이는 side branch가 일괄 정규화되거나 dropout layer가 있는 경우 네트워크의 main classifer가 더 잘 수행된다는 사실에 의해 뒷받침됩니다.
Efficient Grid Size Reduction
representational bottleneck을 피하기 위해, 각 activation dimension이 너무 작아지는 것을 방지해야합니다.
따라서 Average 또는 Maximum Pooling을 적용하기 전에 네트워크 필터의 activation dimension이 확장됩니다.
이때, 우리는 pooling 대신 convolution 연산을 사용합니다.
이렇게 될 경우, filter의 size가 d, 갯수가 k 일때 pooling이 2(d^2)(k^2) operation을 수행하는 반면에 convolution은 2(d/2)^2(k^2) operation을 수행합니다.
그러나! 해당 방법으로는 연산이 줄어들지만 representational bottleneck이 발생할 수 있습니다.
Pooling을 Convolution으로 대체하는 방법 대신에 우리는 그냥 stride를 늘린 pooling 연산을 수행합니다.
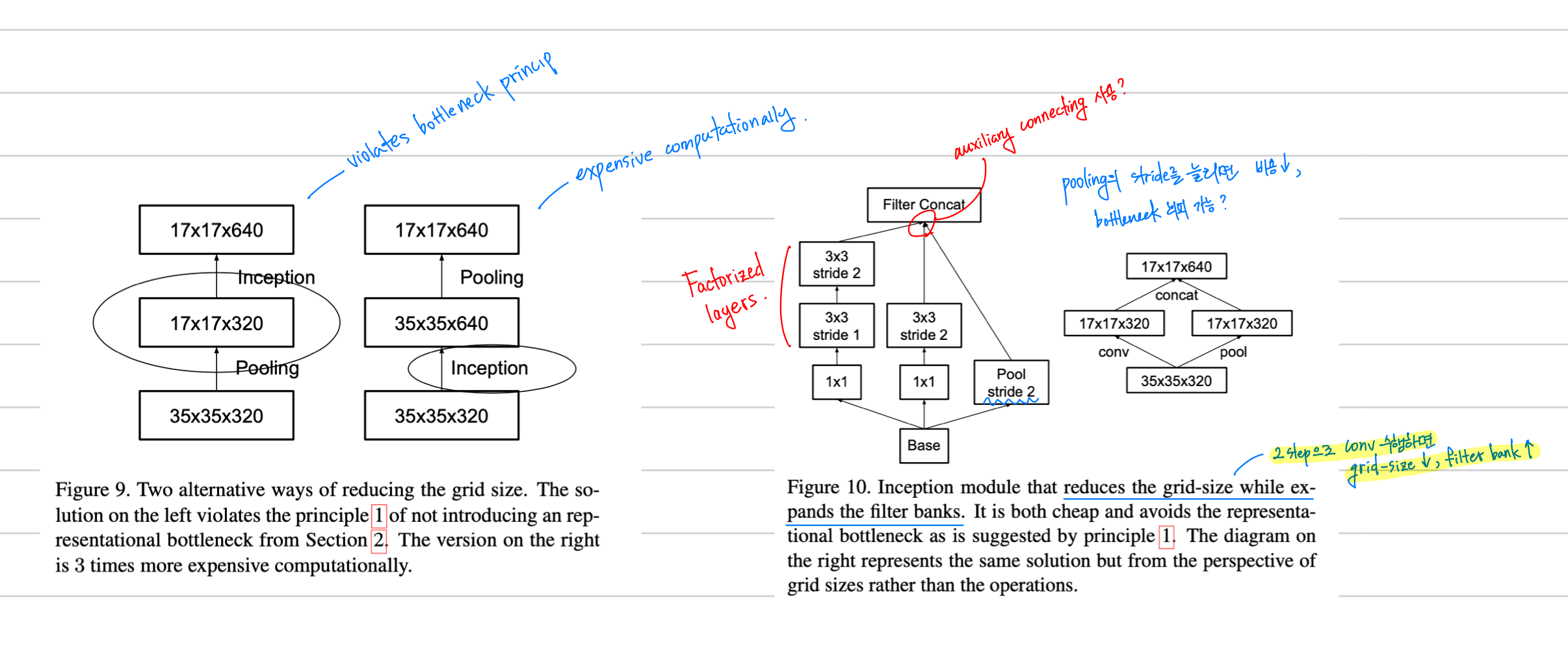
제가 작성한 메모입니다.
Fig 9을 먼저 봐주시길 바랍니다.
좌측 모델의 경우 급격한 bottleneck 구조를 가지고 있습니다.
activation dimension이 너무나 줄어들기에 좋지 않습니다. 이는 bottleneck principle을 위반합니다.
우측 모델의 경우 고비용의 연산을 수행합니다. 지양해야합니다.
Fig 10을 봐주시길 바랍니다.
이전에 첨부한 모델 그림과 같은 모델이 있습니다.
Convolution을 Factorize하여 동일한 효과를 얻음과 동시에 Computational Cost를 줄였습니다.
이때, Factorization을 수행하였기 때문에 더 많은 activation dimension도 확보하였을 것 입니다.
성능의 개선도 기대해볼 수 있겠군요.
Pooling 연산을 수행하지만 stride를 늘려 비용도 줄이고 bottleneck도 회피하였습니다.
이를 auxiliary connection로 연결하여 regularizer의 효과도 얻습니다.
모든 연산이 진행된 후 filter를 concat하여 앞서 말한 방법대로 모델을 구성하였습니다.
동일한 혹은 더 우월한 성능을 가짐과 동시에 computational cost도 절약하였습니다.
Model Regularization via Label Smoothing
이번에는 조금은 색다른 방법으로 classifer layer를 regularize하는 매커니즘에 대해 알아봅니다.
해당 매커니즘은 훈련 도중에 label-dropout의 marginalized effect를 추정하는 것으로 regularization을 진행합니다.
기존에는 각 label에 대한 ground truth distribution의 cross-entropy log-likelihood의 maximized value를 계산하였습니다.
그러나 이것은 너무 confident합니다.
물론 이것이 의도한 목적이라면 해당하지 않겠지만 논문에서는 새로운 방법을 제시합니다.
다음은 각 매개변수에 대한 설명입니다.
distribution of labels : u(k)
smoothing parameter : epsilon
ground truth label : y
label distribution = 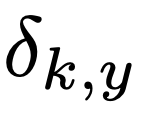 with
with
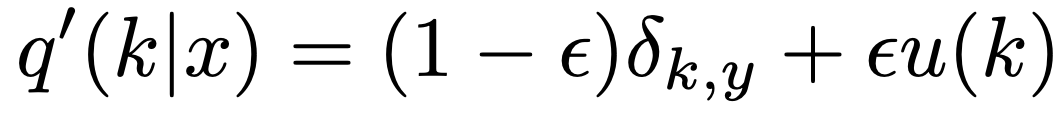
이는 원래의 실측 분포 q(k|x)와 고정 분포 u(k)와 각각 가중치 (1-epsilon) 및 epsilon를 혼합한 것입니다.
우리는 실제 라벨 분포의 이러한 변화를 label-smoothing regularization 또는 LST라고 부릅니다. LSR은 max logit이 다른 모든 logit보다 훨씬 커지는 것을 방지한다는 원하는 목표를 달성합니다.

따라서 LSR은 단일 교차 엔트로피 손실 H(q, p)를 이러한 손실 H(q, p) 및 H(u, p) 쌍으로 대체하는 것과 동일합니다.
