
U-net은 Image Segmentation를 위한 딥러닝 아키텍처 중 하나로, 2015년에 발표된 모델입니다.
해당 모델은 이미지 내의 픽셀 수준에서 객체를 정확하게 분할할 수 있으며, 의료 영상, 자율 주행 자동차, 지리 정보 시스템 등 다양한 분야에서 활용됩니다.
Introduction
논문에서 해당 챕터는 Image Segmentation을 다룬 이전 모델의 방법들과 장단점을 소개하며 시작합니다.
하지만 해당 글에서는 그것을 언급하지 않고 오롯이 U-Net에 대한 내용만 작성하도록 하겠습니다.
"In this paper, we build upon a more elegant architecture, the so-called “fully convolutional network”. We modify and extend this architecture such that it works with very few training images and yields more precise segmentations"
위 글에서 알 수 있듯 U-Net은 Dense Layer 없이 Convolutional Layer로만 구성된 모델입니다.
또한 매우 적은 훈련 데이터셋으로도 정확한 Segmentation 작업이 가능합니다.

U-Net은 Encoder-Decoder 기반 모델이며 몇가지 변형이 존재합니다.
(U-Net에서 Encoder는 Contracting Path, Decoder는 Expansive Path라고 지칭합니다.)
기존 Encoder-Decoder 모델은 대상의 특징을 효율적으로 추출하여 작업을 수행할 수 있다는 장점이 있습니다.
그러나 차원 수를 점점 줄여나가기 때문에 객체의 위치 정보를 잃게 됩니다. 그렇기 때문에 모델의 고차원 데이터의 정보를 제대로 활용하지 못합니다.
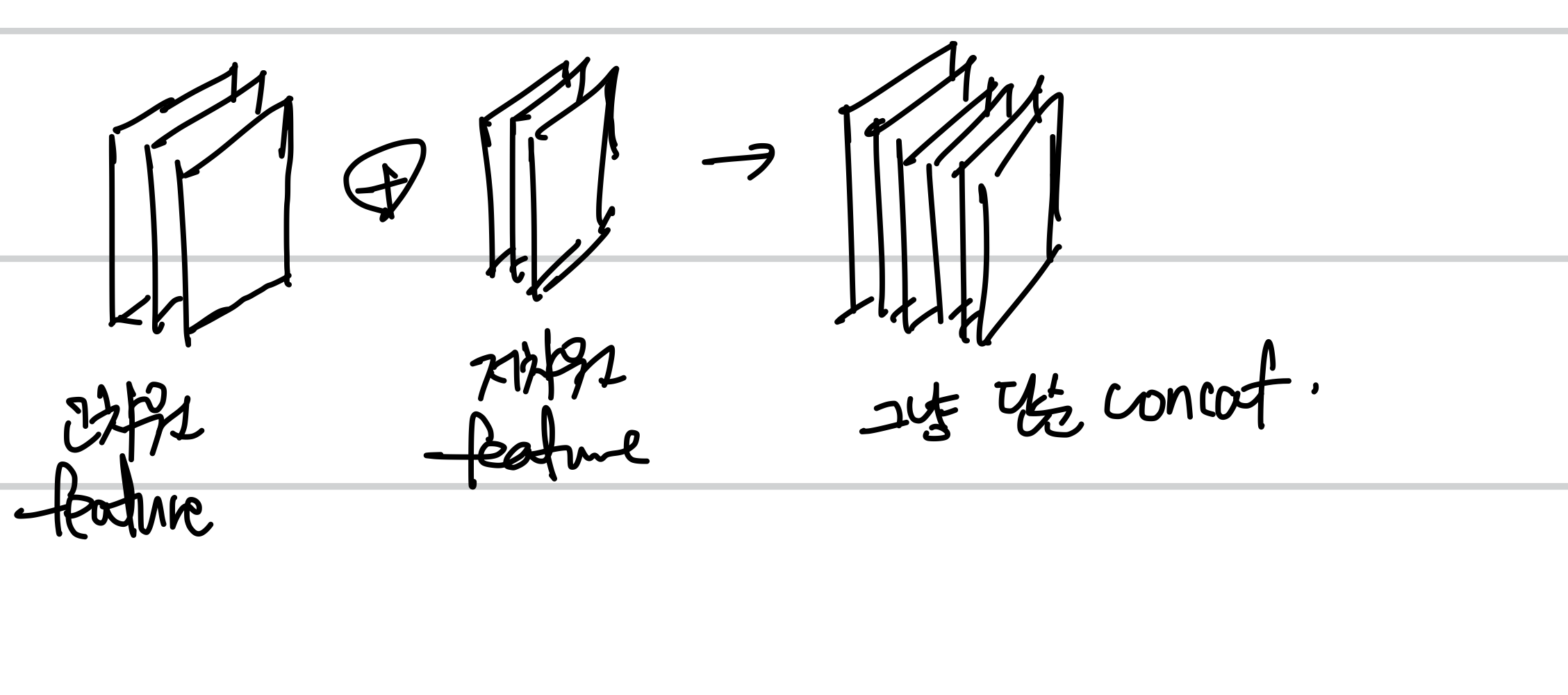
U-Net은 Encoding 단계의 각 데이터에서 얻은 특징을 Decoding 단계의 각 레이어에 Concatentate하여 해당 단점을 극복합니다. Encoding, Decoding Layer 사이는 skip connection을 통해 연결되며 이때 각 Layer는 대칭적입니다.
(skip connection한 2개의 feature map을 단순 concat하여 하나의 feature map으로 사용합니다.)
(+이미지의 경계 영역에 있는 픽셀을 예측하기 위해 입력 이미지를 미러링하여 누락된 컨텍스트를 추정합니다.)
일반적인 CNN 모델은 Convolutional Layer와 Pooling Layer로만 구성됩니다.
U-net은 Expansive Path에서 Pooling Layer를 사용하지 않고 이를 Upsampling Layer로 대체합니다.
이는 출력의 해상도를 높여줍니다.
대상 객체의 위치 파악(localize)을 위해 contracting path에서 추출된 고해상도 특징이 Upsampling된 출력과 결합됩니다. 그런 다음 연속적인 컨볼루션 레이어는 이 정보를 기반으로 보다 정확한 출력을 조합하는 방법을 학습할 수 있습니다."
U-Net의 한 가지 중요한 수정 사항은 Upsampling 부분에 네트워크가 컨텍스트 정보를 더 높은 해상도 레이어에 전파할 수 있도록 하는 많은 수의 기능 채널도 있다는 것입니다.
지금까지 말한 U-net 모델의 특징을 생각하며 모델 구조 이미지를 다시 한번 살펴봅니다.

Encoder-Decoder 구조를 띄고 있으며 Pooling 대신 Upsampling을 사용합니다.
저차원으로 갈수록 많은 양의 feature map을 보유합니다.
Contracting Path와 Expansive Path는 서로 대칭적이며 Skip connection으로 연결됩니다. 이를 통해 고차원의 feature map을 가져와 위치 파악에 활용합니다.
Network Architecture
Contracing Path
2개의 3x3 Unpadded convolution layer, rectified liner unit (ReLU), 다운샘플링을 위한 2x2 MaxPooling (stride=2) 의 연속된 구조로 구성되어 있습니다.
각 다운샘플링 단계마다 우리는 feature channels의 수를 2배로 늘립니다.
Expansive Path
Expansive Path의 각 단계는 feature channel의 수를 절반으로 줄이고 feature map을 upsampling하며 대응하는 Contracting Path의 feature map을 concat하는 2X2 Up-conv Layer, 2개의 3x3 Conv, ReLU의 반복으로 구성됩니다.
at the final layer...
최후에는 1x1 conv가 각 64-component feature vector를 원하는 수만큼의 class에 매핑하기 위해 존재합니다.
Training
에너지 함수는 cross-entropy function과 결합된 최종 feature map에 대해 픽셀별 softmax로 계산됩니다.
Optimizer는 SGD, Loss Function은 앞서 언급되었듯 Cross-Entropy loss function입니다.
훈련 데이터 세트의 특정 클래스에서 픽셀의 다양한 빈도를 보상하고 접촉 셀 사이에 도입하는 작은 분리 경계를 네트워크가 학습하도록 강제하기 위해 각 실측 분할에 대한 가중치 맵을 미리 계산합니다
분리 경계는 Mophological Operations(형태학적 작업)를 통해 계산됩니다.
그리고 가중치 맵은 다음의 공식으로 계산됩니다.
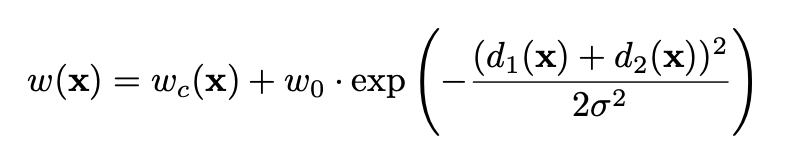
각각 parameter는 다음에 대응됩니다.
Wc : class frequency를 균형잡기 위한 weight map입니다.
d1 : 가장 가까운 셀의 경계와의 거리입니다.
d2 : 2번째로 가까운 셀의 경계와의 거리입니다.
논문에서는 W0 = 10, std = 5 pixel 로 설정하였습니다.
Weight Initializing?
많은 양의 Conv Layer를 사용하는 심층 신경망에서 Weight map을 올바르게 초기화하는 것은 매우 중요합니다.
그렇지 않을 경우 신경망이 수렴하지 않거나 과도하게 활성화 될 수 있습니다.
이상적으로는 네트워크의 각 feature map이 대략적인 단위 분산을 갖도록 초기 가중치를 조정해야 합니다. 우리 아키텍처(컨볼루션 및 ReLU 레이어가 교대로 반복됨)를 사용하는 네트워크의 경우 표준 편차가 sqrt(2/N)인 Gaussian Distribution에서 초기 가중치를 도출하여 이를 달성할 수 있습니다. 여기서 N은 뉴런 하나의 들어오는 노드 수를 나타냅니다.
Ex) 3x3 conv, 64 feature channels이 이전 레이어에 존재한다면, N = (3x3)x64 = 9x64 = 576.
Data Augmentation
데이터 증감은 주어진 데이터셋의 크기가 작을 경우 필수적이다.
Microscopical Images에서는 주로 이동 및 rotation invariance (회전 불변) 뿐만 아니라 변형 및 gray value 변화에 대한 견고성이 필요합니다.
특히 훈련 샘플의 무작위 탄성 변형은 주석이 달린 이미지가 거의 없는 분할 네트워크를 훈련하는 핵심 개념인 것 같습니다. 우리는 거친 3x3 그리드에서 무작위 변위 벡터를 사용하여 부드러운 변형을 생성합니다.
변위는 10픽셀 표준편차를 갖는 가우스 분포에서 샘플링됩니다. 그런 다음 bicubic interpolation(쌍입방 보간법)을 사용하여 픽셀당 변위를 계산합니다. 축소 경로 끝에 있는 드롭아웃 레이어는 추가 암시적 데이터 증대를 수행합니다.
Bicubic Interpolation? (쌍입방 보간법?)
ChatGPT를 통해 배워봅시다.
쌍선형 보간법은 이미지의 크기를 변경할 때 사용되며, 원본 이미지의 픽셀 값들로부터 새로운 픽셀 값을 예측하여 새로운 이미지를 생성하는 과정입니다. 이때, 새로운 이미지의 크기가 원본 이미지보다 크거나 작은 경우에도 적용할 수 있습니다.
이 과정에서 쌍선형 보간법은 대상 픽셀 주변의 이웃 픽셀들의 값을 이용하여 보간값을 계산합니다. 대상 픽셀이 이웃 픽셀 사이에 위치할 때, 이웃 픽셀들의 값을 이용하여 대상 픽셀의 보간값을 결정하는 것입니다.
이때 사용되는 수식은 다음과 같습니다:
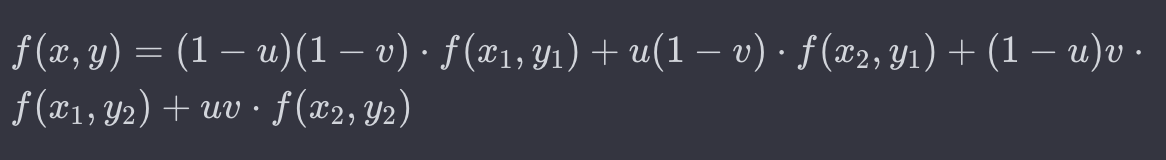
여기서 f(x, y) 는 보간된 값, (x, y)는 대상 픽셀의 좌표를 나타냅니다. u와 v는 대상 픽셀과 가장 가까운 왼쪽 이웃 픽셀까지의 거리에서의 상대적 위치를 나타냅니다. f(x1, y1), f(x2, y1), f(x1, y2), f(x2, y2)는 대상 픽셀 주변의 이웃 픽셀들의 값입니다.
이 수식은 대상 픽셀과 이웃 픽셀들 간의 거리와 상대적인 위치를 고려하여 가중 평균을 계산하고, 이를 통해 대상 픽셀의 보간값을 결정합니다. 이러한 방식으로 쌍선형 보간법은 이미지의 크기를 변경할 때 부드럽고 자연스러운 결과를 얻을 수 있습니다.
음.. 해당 개념은 이해가 잘 되질 않는군요.. 우선 묵혀두고 이후 읽을 논문에서 반복해서 제시된다면 따로 공부를 해보겠습니다.
