정렬 Sort (JAVA)

1. 버블 정렬

• 데이터의 인접 요소기리 비교하고, swap 연산을 수행하며 정렬하는 방식
• 시간 복잡도 : O(n2) 다른 정렬에 비해 느리다.

위와 같은 과정을 오름차순/내림차순으로 정렬될 때까지 반복한다.

오름차순 정렬
for (int i=0; i<N-1; i++) {
	for (int j=0; j<N-i-1; j++) { 
    	if (A[j] > A[j+1]) { // 정렬
        	int temp = A[j];
            A[j] = A[j+1];
            A[j+1] = temp;
		}
	}
}

2. 선택 정렬

• 대상에서 최대나 최소 데이터를 찾아가 선택을 반복하며 정렬하는 방식
• 구현이 복잡하다
• 시간 복잡도 : O(n2)

오름차순 정렬
for (int i=0; i<length; i++) {
	int min = i;
    for (int j=i; j<length; j++) {
    	if (A[j] < A[min])  // 최솟값을 찾기
        	min = j;
    }
    if (A[i] > A[min]) { // 정렬
    	int temp = A[i];
        A[i] = A[min];
        A[min] = temp;
   	}
}

3. 삽입 정렬

: 대상을 선택해 정렬된 영역에서 선택 데이터의 적절한 위치를 찾아 삽입하면서 정렬하는 방식

오름차순 정렬
for (int i = 1; i < length; i++) {
	int temp = A[i];
    int j = i - 1;
    while (j >= 0 && tmp < A[j]) {
		A[j + 1] = A[j];
		j--;
	}
	A[j + 1] = tmp;
}

4. 퀵 정렬

: pivot 값을 선정해 해당 값을 기준으로 해당 값보다 작은 데이터와 큰 데이터로 분류하여 정렬하는 방식

오름차순 정렬
public static void quickSort(int start, int end) {
    if(start >= end)  return; 

    int pivot = A[ ( start + end ) / 2 ];
    int left = start;
    int right = end;

    while(left <= right) {
        while(A[left] < pivot) left ++;
        while(A[right] > pivot) right --;

        if(left <= right) {
            int temp = A[right];
            A[right] = A[left];
            A[left] = temp;
            left++;
            right--;
        }
    }

    if(start < right) quickSort(start, right);
    if(left < end) quickSort(left, end);
}

5. 병합 정렬

: 분할 정복 방식을 이용하여 데이터를 분할하고 분할한 데이터를 정렬하며 병합하는 방식

오름차순 정렬
public static void mergeSort(int start, int end) {
	if (end - start <1 ) return;
    int mid = start + (end - start)/2;
    mergeSort(start, mid);
    mergeSort(mid+1, end);
	
    for(int i = start ; i <= end ; i ++) {
        temp[i] = A[i];
    }
    int k = start;
    int x = start;
    int y = mid + 1;
    while(x <= mid && y <= end) {
        if(temp[x] < temp[y]) {
            A[k++] = temp[x++];
        } else {
            A[k++] = temp[y++];
        }
    }
    while(x <= mid) {
        A[k++] = temp[x++];
    }
    while(y <= end) {
        arr[k++] = temp[y++];
    }
}

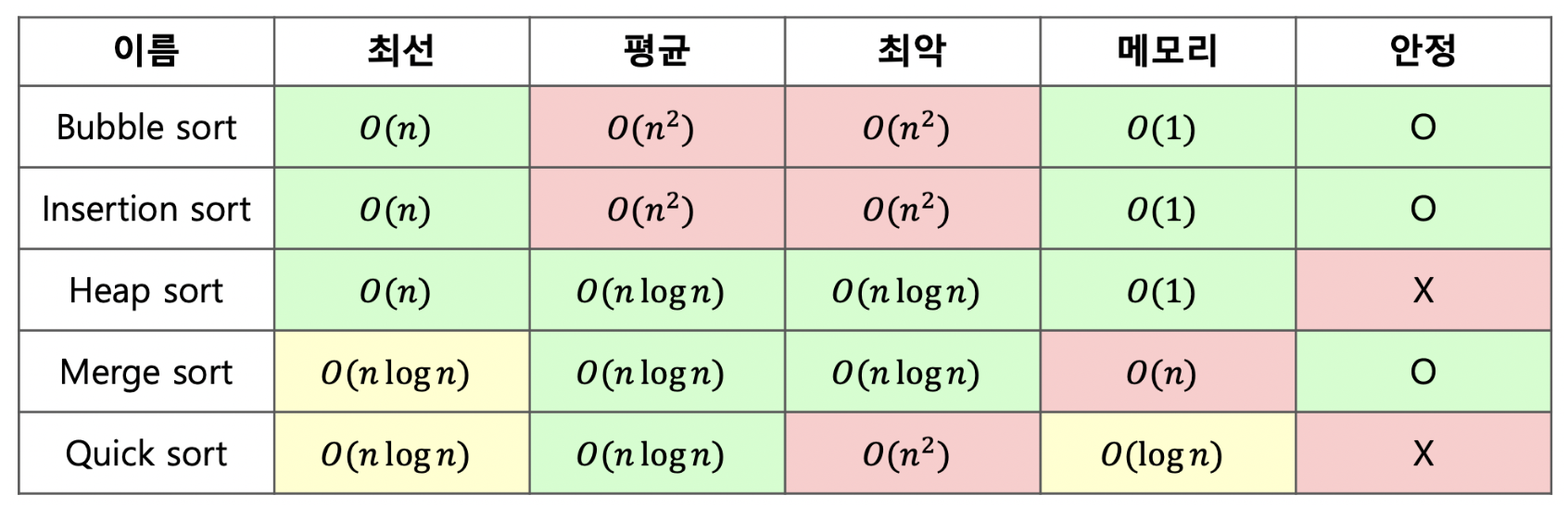
6. 시간복잡도

사진 출처