동적 계획법(Dynamic Programming)

동적 계획법(Dynamic Programming)

동적 계획법 : 어떤 문제를 여러 개의 작은 문제로 나눠 해결하고 그 결과를 저장 했다가 큰 문제를 풀 때 사용하는 문제 풀이 기법

• 계산한 건 다시 계산하지 않는 것이 중요!!
• 메모리 공간을 약간 더 사용해서 연산 속도를 비약적으로 증가시킨다.

DP vs 분할 정복❓

• 분할 정복 : 해결한 문제를 반복적으로 해결
• DP : 이미 푼 문제는 기억하여 다시 풀지 않음
• 즉, 부분 문제가 중복된다면 DP가 더 효율적

DP 사용 조건

1. 최적 부분 구조

• 큰 문제를 작은 문제로 나눌 수 있다.

2. 겹치는 부분 문제

• 동일한 작은 문제들이 중복되어 사용되는 경우 사용 가능.

피보나치 수열

• DP로 해결할 수 있는 가장 대표적인 예시!

---

피보나치 수열 점화식

---

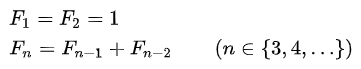
이걸 재귀함수로 구현하면, 다음과 같다.

def fibo(n):
	if n==1 or n==2:
    	return 1
    return fibo(n-1) + fibo(n-2)

• 해당 코드는 O(2^n)의 시간복잡도를 가지게 되어, n이 증가할수록 수행 시간이 기하급수적으로 늘어난다.
• 피보나치수열 문제는 작은 문제의 답이 그것을 포함한 큰 문제에서도 답이 되고, 동일한 작은 부분 문제들이 중복되어 사용되므로 DP의 두 조건을 만족한다.
• DP를 사용해 피보나치 수열을 작성해보자.

Top-Down 방식

• 메모이제이션을 사용해 다이나믹 프로그래밍을 구현하는 방식 중 하나

메모이제이션 : 한 번 구한 계산 결과를 메모리 공간에 메모해두고, 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법

• 탑다운 방식은 큰 문제를 해결하기 위해 작은 문제를 호출한다고 하여 하향식이라고도 불린다.
• 재귀함수를 이용해 구현할 수 있다.

# DP 
# memoization (하향식)

dp = [0]*100 # 소문제 결과를 저장할 리스트
dp[0] = 1 
dp[1] = 1

def fib(n):
    
    # 만약 계산한 적이 없다면 재귀로 계산 
    if dp[n] == 0:
        dp[n] = fib(n-1) + fib(n-2)
    
    # 있다면 그대로 반환 
    return dp[n]

fib(10)

Bottom-Up 방식

• 더 작은 하위 문제부터 살펴본 다음 작은 문제의 정답을 이용해 큰 문제의 정답을 풀어나가는 방법
• 상향식, 타뷸레이션이라고도 함

# DP
# 타뷸레이션 (상향식)

def fib(n):

    dp = [0]*(n+1)
    dp[0] = 1
    dp[1] = 1
    
    # 작은 값(소문제)부터 직접 계산하며 진행 
    for i in range(2,n+1):
        dp[i] = dp[i-1] + dp[i-2]
    
    return dp[n]

fib(10)

참고

https://c4u-rdav.tistory.com/37
https://doing7.tistory.com/75
https://lsh424.tistory.com/76