트리
- 계층적 구조 표현
트리 관련 용어
- 노드(node): 실제로 저장하는 데이터
- 루트(root) 노드: 최상위에 위치한 데이터
- 시작 노드
- 모든 노드와 직간접적으로 연결됨
- 리프(leaf) 노드: 마지막에 위치한 데이터들
- 더 이상 가지 치지 않음
- 부모-자식: 연결된 노드들 간의 상대적 관계
- 자식은 없을 수도, 많이 있을 수도
- 부모는 언제나 1개
- 트리가 그래프보다 더 제약이 있다.
- 깊이(depth): 노드 -> 루트 경로의 길이
- 높이(height): 노드-> 리프 경로의 최대 길이
- 레드 블랙트리에서 사용
- 하위 트리(subtree): 어떤 노드 아래의 모든 것을 포함하는 트리
- 재귀적: 하위 트리 그 자체가 트리
트리의 속성
- 부모와 자식 모두 노드
- 부모:자식 = 1: 다수
- 자식은 언제나 부모로부터 가지를 침
이진트리
- 자식이 최대 둘(왼쪽, 오른쪽)
- 무언가 계층적으로 이분해 나갈 때 적합
이진 탐색 트리(binary search tree, BST)
- 가장 많이 사용하는 트리
- 왼쪽 자식은 언제나 부모보다 작다, 오른쪽자식은 언제나 부모이상
- 정렬된 트리 - 재귀적으로 읽으면(중위순회)
- 정렬되어 있으니 효율적인 알고리즘 사용 가능
- 평균 삽입, 삭제, 탐색시간 O(logn)
- 최악의 경우 O(n): 한쪽에 줄줄이 있을 때
BST 탐색
- 이진 탐색 트리의 겨웅 왼쪽 하위 트리는 항상 나보다 작고 오른쪽 하위 트리는 크기 때문에 따라가면 탐색할 수 있음.
BST 삽입
- 새로운 노드를 받아줄 수 있는 부모 노드를 찾음
- 탐색과 방법이 같음.
- 새로운 노드를 받아줄 수 있는 부모 -> 오른쪽 하위트리로 가야하는데 오른쪽 자식이 없는부모, 왼쪽 하위트리로 가야하는데 왼쪽 자식이 없는 부모
- 자식 추가
BST 삭제
- 리프노드의 경우
- 리프노드는 그냥 삭제
- 자식이 있는 노드의 경우
- 트리에서는 무언가를 지울 때 항상 리프를 지움.
- 정렬 된 배열로 생각 하면 쉽다.
- 오른쪽 하위 트리에서의 최솟값 -> in order successor
- 왼쪽 하위 트리에서 최댓값 -> in order predecessor
순서
1. 지울 값을 가지고 있는 노드를 찾는다
2. 그 바로 전 값을 가진 노드를 찾는다.
- 왼쪽 하위 트리의 제일 오른쪽 리프 or 오른쪽 하위 트리의 제일 왼쪽 리프
3. 두값을 교환
4. 리프노드삭제
순회 방법(이름은 내노드를 기준으로 생각)
1. 중위 순회(in-order traversal)
- 왼쪽 하위 -> 현재 -> 오른쪽 하위트리
2. 전위(pre-order) 순회
- 현재 -> 왼쪽 -> 오른쪽
- 이진탐색에서 잘 쓰지 않음.
- 용도
- 트리 복사(다른 순회도 가능하지만 직관적이지 않음)
- 수식은 보통 중위 표기법을 사용 -> 전위 표기법으로 표기하면 컴퓨터로 계산하기 좀더 편함.
3. 후위(post-order) 순회
- 왼쪽 -> 오른쪽 -> 현재
- 위의 전위 2번째 용도는 후위 순회로 표현시 더 쉽게 구현
레드-블랙 트리(red-black tree)

- 각 노드가 레드 혹은 블랙(노드에 저장하는 데이터 X)
- 그냥 1비트 짜리 정보
- 스스로 균형을 잡는(self-balancing) 트리
- 최소한의 트리 높이를 보장
- 균형을 잡는 시점-> 삽입, 삭제
- 그 외 연산은 BST와 동일( 탐색 속도는 더 빠르다)
- C++ STL의 set, multiset, map, and multimap 이 이 레드 블랙 트리를 이용하여 구현
레드-블랙 트리(red-black tree)의 특성
- 모든 노드는 레드 혹은 블랙이다(Nil 노드 포함)
- 루트 노드는 언제나 블랙
- 모든 리프 노드(Nil)는 블랙이다. 즉 Nil 노드가 리프노드임.
- 레드 노드의 자식은 모두 블랙이다
- 어떤 노드와 리프 사이에 있는 블랙 노드 수는 동일하다(중요).
- 이를 통해 블랙과 레드 노드의 수의 균형 맞음
- 리프 노드는 데이터를 담지 않음(Nil)
- 블랙 깊이(black depth): 루트와 어떤 노드 사이에 있는 블랙 노드 수
- 블랙 높이(black height): 어떤 노드와 리프 사이에 있는 블랙 수
- 가장 큰 리프 깊이가 가장 작은 것의 2배를 넘지 않는다.
- 트리가 한쪽으로 쏠리는 것을 방지 -> O(logn) 보장
레드-블랙 트리(red-black tree)의 연산
탐색
- 이진 탐색 트리와 동일
- 단 logn을 보장
삽입&삭제
- 무작정 삽입하거나 삭제 ->특성이 망가짐
- 망가진 특성을 고치려 트리 구조 재배치(회전) 혹은 노드 색 변환
- 삽입 삭제 O(logn) 고정
AVL 트리(Adelson-Velsky and Landis tree)
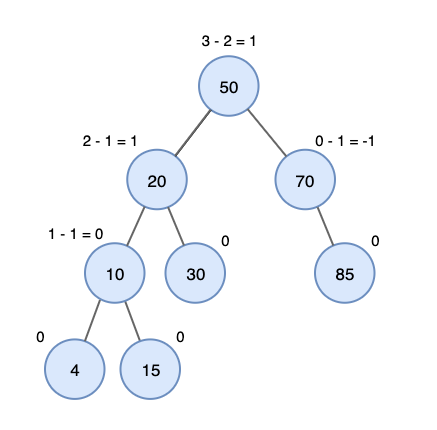
- BST 트리의 경우 최악의 경우 O(n)의 시간 복잡도를 보이는데 이것을 방지하고자 스스로 균형을 잡는 이진 탐색 트리
- 두 자식 서브 트리의 높이는 항상 최대 1만큼 차이 난다.
- 레드 블랙트리와 비슷하나 BF(balance Factor)를 통해 균형을 잡는다.
