그래프
- 데이터(노드)들을 잘 정리하는(노드간의 관계를) 방법 중 하나
- 데이터들과 그 관계를 보여주는 방법 중 하나
- 서로 연관 있는 노드의 집합
- G = (N, E)
- 네트워크 형태의 관계를 보여주기에 적합
용어
- 노드(정점, 꼭짓점)
- 변(간선, 선)
- 차수(degree) : 나한테 몇개 연결되어 있나
- 루프(loop): 자기자신한테 돌아오는것
그래프의 종류
- 방향/무방향(directed/undirected) 그래프
- 순환/비순환(cyclic/acyclic) 그래프
- 가중/비가중(weighted/unweighted) 그래프
무방향 그래프의 최대 변 개수
- 모든 노드가 연결되어 있는 경우
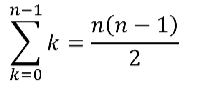
그래프의 표현 방법
- 인접 행렬
- N * N 행렬
- G[N][N]
- N: 그래프 G안에 있는 노드수
- 서로 인접한 노드를 표현
- i → j로 향하는 변이 있다: G[i][j] = 1
- G가 가중 그래프라면 실제 가중치 저장
- 관계 찾는거 O(1)
- 단점
- 메모리를 많이 차지함.
- N * N 행렬
- 인접 리스트
- 각 노드마다 이웃의 리스트를 만듦
- 리스트 N 개
- 장점: 공간 적게 사용
- O(N + E)
- 최악 O(N제곱)
- 삽입/삭제가 빠름.
- 단점:
- O(1)보다 관계찾는것이 느림.
DFS(Depth-first Search, 깊이 우선 탐색)
- 트리에서의 DFS와 달리 그냥 탐색을 해버리면 무한 루프 생성 가능
- 따라서 방문했던 노드를 기억해야 한다.
- 그래프 DFS의 시간 복잡도: O(N + 2E) == O(N + E)
- 각 노드는 최대 한 번 처리됨 → O(N)
- 각 변은 최대 두 번 고려됨 → O(2E)
def DFS(node):
stack = []
stack.push(node)
while stack:
current = stack.pop()
if visited[current] == True:
continue
visited[current] = True
print(node)
for e in edge[node]:
stack.append(e)BFS(Breadth-First Search, 너비 우선 탐색)
- 마찬가지로 트리에서처럼 탐색 해버리면 무한 루프 생성
- 방문했던 노드 기억
- 시간복잡도: O(N + E)
def BFS(node):
queue = deque()
queue.push(node)
while queue:
current = queue.popleft()
if visited[current] == True:
continue
visited[current] = True
print(node)
for e in edge[node]:
queue.append(e)MST(최소 신장 트리, Minimum Spanning Tree)
- Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리
신장 트리(Spanning Tree)
- 어떤 그래프 안에 있는 모든 노드를 연결하는 트리
- 여러 개 있을 수 있음.
MST 알고리즘 개념
-
순환(cycle) : 시작노드와 끝노드가 같은 것
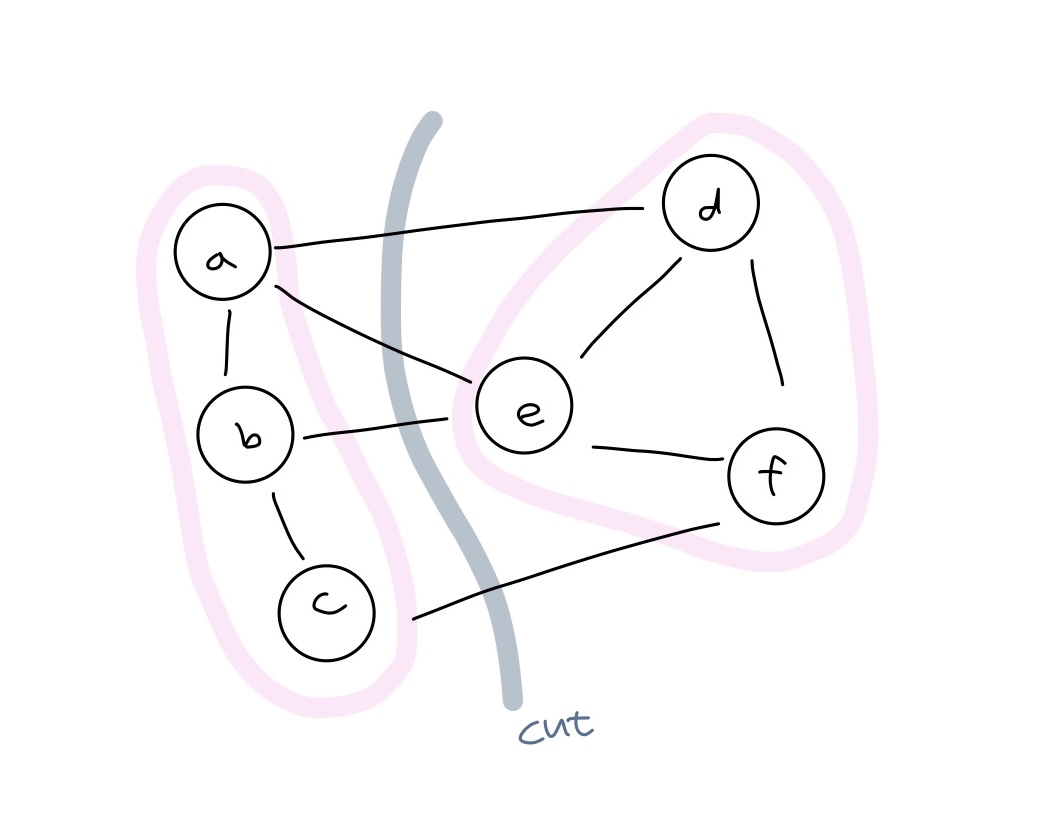
-
컷(cut) : 어떤 그래프를 서로소(disjoint)인 두 하위 조합으로 나누는 행위
-
두 그래프를 두 그룹으로 분리
-
컷-세트(cut-set) : 두 그룹을 연결하는 변들의 집합
-
컷 세트에 가중치가 다른 여러 그래프가 있다면 MST에 포함되는 것은 가장 가중치가 작은 변
-
알고리즘 순서
- 그래프에 있는 노드 중 한 변 확인
- 이 변에 MST에 들어가야 하는 지 검사
- 이 때 cut property 사용
- 들어가야 하면 MST에 추가, 아니면 무시
- MST 의 모든 변을 찾지 못했다면 1로 돌아감
어떤 알고리즘과 비슷한가?
크루스칼 알고리즘
- 그래프의 각 노드마다 그 노드만 포함하는 트리 만듦
- 모든 변을 가중치의 오름차순으로 정렬 → S배열
- S가 비거나 MST가 완성될 때까지 다음 과정을 반복
1. S에서 가중치가 가장 적은 변을 제거해서 고려
2. 이변이 두 트리를 연결하는지 검사
1. 그렇다면 MST에 추가
2. 아니라면 버림
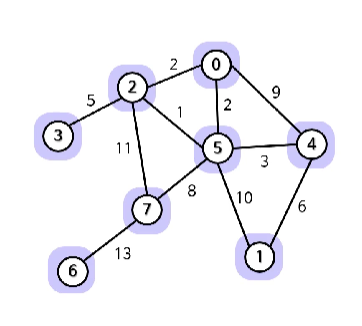
S
1 2 2 3 5 6 8 9 10 11 13
