[JAVA] 컬렉션 프레임워크 - Set

한 줄 요약

• HashSet: 순서 보장 X
• LinkedHashSet : 순서 보장 O
• TreeSet : 정렬된 상태 보장하면서 특성 보장

1. 자바가 제공하는 Set1 - HashSet, LinkedHashSet

Set은 중복을 허용하지 않고, 숫서를 보장하지 않는 자료 구조이다.

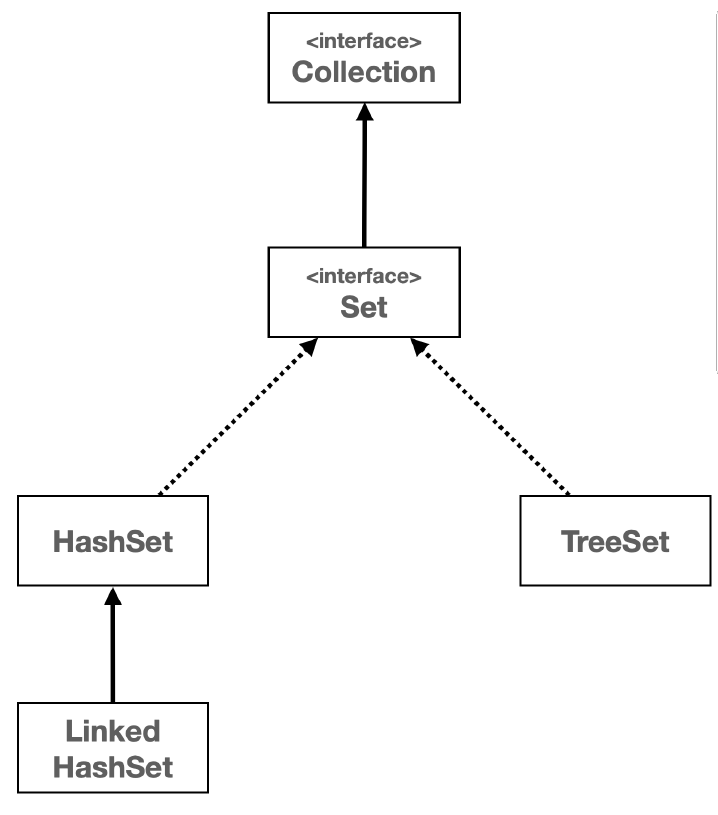
컬렉션 프레임워크 - Set

Collection 인터페이스

• Collection 인터페이스는 java.util 패키지의 컬렉션 프레임워크의 핵심 인터페이스 중 하나이다. 이 인터페이스는 자바에서 다양한 컬렉션, 즉 데이터 그룹을 다루기 위한 메서드를 정의한다.
• Collection 인터페이스는 List , Set , Queue 와 같은 다양한 하위 인터페이스와 함께 사용되며, 이를 통해 데이터를 리스트, 세트, 큐 등의 형태로 관리할 수 있다.

지금부터 Set 의 주요 구현체를 하나씩 알아보자.

• HashSet
• LinkedHashSet
• TreeSet

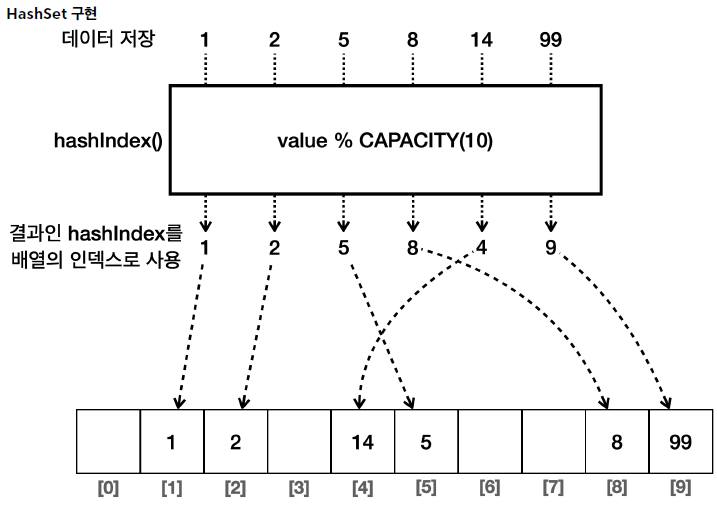
1) HashSet

• 구현 : 해시 자료 구조를 사용해서 요소를 저장한다.
• 순서 : 요소들은 특정한 순서 없이 저장된다. 즉, 요소를 추가한 순서를 보장하지 않는다.
• 시간 복잡도 : HashSet의 주요 연산은 평균적으로 O(1) 시간 복잡도를 가진다.
• 용도 : 데이터의 유일성만 중요하고, 순서가 중요하지 않은 경우에 적합하다.

• 그림을 단순화 했지만, hashCode(), equals()를 모두 사용한다.

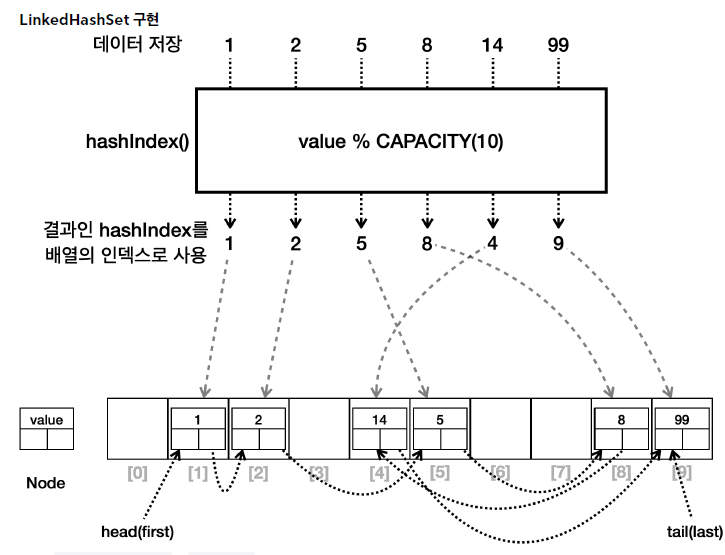
2) LinkedHashSet

• 구현: LinkedHashSet 은 HashSet 에 연결 리스트를 추가해서 요소들의 순서를 유지한다.
• 순서: 요소들은 추가된 순서대로 유지된다. 즉, 순서대로 조회 시 요소들이 추가된 순서대로 반환된다.
• 시간 복잡도: LinkedHashSet 도 HashSet 과 마찬가지로 주요 연산에 대해 평균 O(1) 시간 복잡도를 가진다.
• 용도: 데이터의 유일성과 함께 삽입 순서를 유지해야 할 때 적합하다.
• 참고: 연결 링크를 유지해야 하기 때문에 HashSet 보다는 조금 더 무겁다.

• LinkedHashSet은 HashSet에 연결 링크만 추가한 것이다.
• HashSet에 LinkedList를 합친 것으로 이해
• 이 연결 링크는 데이터를 입력한 순서대로 연결ㄹ된다.
  • head(first) 부터 순서대로 링크를 따라가면 입력 순서대로 데이터를 순회할 수 있다.
  • 양방향으로 연결된다.
• 이 링크를 first 부터 순서대로 따라가면서 출력하면 순서대로 출력할 수 있다.

2. 자바가 제공하는 Set2 - TreeSet

3) TreeSet

• 구현 : TreeSet 은 이진 탐색 트리를 개선한 레드-블랙 트리를 내부에서 사용한다.
• 순서: 요소들은 정렬된 순서로 저장된다. 순서의 기준은 비교자( Comparator )로 변경할 수 있다. 비교자는 뒤에서 다룬다.
• 시간 복잡도: 주요 연산들은 O(log n) 의 시간 복잡도를 가진다. 따라서 HashSet 보다는 느리다.
• 용도: 데이터들을 정렬된 순서로 유지하면서 집합의 특성을 유지해야 할 때 사용한다. 예를 들어, 범위 검색이나 정렬된 데이터가 필요한 경우에 유용하다. 참고로 입력된 순서가 아니라 데이터 값의 순서이다. 예를 들어 3, 1, 2 를 순서대로 입력해도 1, 2, 3 순서로 출력된다.

트리 구조
TreeSet 을 이해하려면 트리 구조를 먼저 알아야 한다.

• 트리는 부모 노드와 자식 노드로 구성된다.
• 가장 높은 조상을 루트라 한다. 이 그림을 뒤집어보면 왜 트리라고 하는지, 처음을 루트라고 하는지 이해가 될 것이다.
• 자식이 2개까지 올 수 있는 트리를 이진 트리라 한다.
• 여기에 노드의 왼쪽 자손을 더 작은 값을 가지고, 오른쪽 자손을 더 큰 값 가지는 것을 이진 탐색 트리라 한다.
• TreeSet 은 이진 탐색 트리를 개선한 레드-블랙 트리를 사용한다.

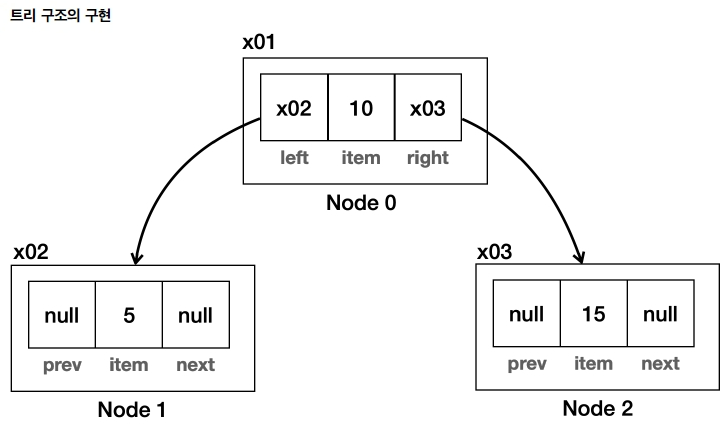
트리 구조의 구현(이진 탐색 트리의 원리)

class Node {
	Object item;
    Node left;
    Node right;
}

• 트리 구조는 왼쪽, 오른쪽 노드를 알고 있으면 된다.
• 앞서 다룬 연결 리스트의 구현을 떠올려보면 쉽게 이해가 될 것이다.

이진 탐색 트리의 계산

이진 탐색 트리 계산의 핵심은 한번에 절반을 날린다는 점이다. 계산을 단순화 하기 위해 16개의 데이터가 있다고 가정하자.

• 16개의 데이터가 있다. 루트에서 처음 비교를 통해 절반의 데이터를 찾지 않아도 된다. 따라서 16 / 2 = 8이 된다.
• 8개의 데이터가 있다. 비교를 통해 절반의 데이터만 남는다. 따라서 8 /2 = 4가 된다.
• 4개의 데이터가 있다. 비교를 통해 절반의 데이터만 남는다. 따라서 4 / 2 = 2가 된다.
• 2개의 데이터가 있다. 비교를 통해 절반의 데이터만 남는다. 따라서 2 / 2 = 1이 된다.
• 1이 남았으므로 이 값이 맞는지 확인하면 된다.

이진 탐색 트리의 빅오 - O(log n)

• 16개의 경우 단 4번의 비교 만으로 최종 노드에 도달할 수 있다.
• 데이터의 크기가 늘어나도 늘어난 만큼 한 번의 계산에 절반을 날려버리기 때문에, O(n)과 비교해서 데이터의 크기가 클 수록 효과적이다.

하지만, 트리의 균형이 맞지 않으면 최악의 경우 O(n)의 성능이 나온다.

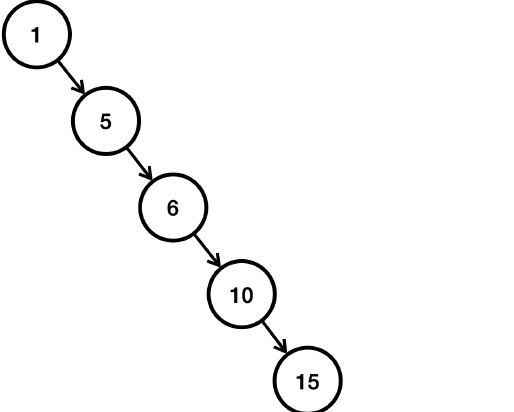
만약 데이터를 1,5,6,10,15 순서로 입력했다고 가정해보자.

• 이렇게 오른쪽으로 치우치게 되면, 결과적으로 15를 검색했을 때, 데이터의 수인 5만큼 검색을 해야 한다.
• 따라서, 이런 최악의 경우 O(n)의 성능이 나온다.

이진 탐색 트리 계선
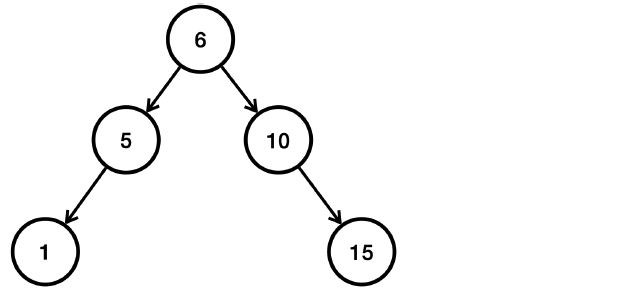
이런 문제를 해결하기 위한 다양한 해결 방안이 있는데 트리의 균형이 너무 깨진 경우 동적으로 균형을 다시 맞추는 것이다.

• 앞서 중간에 있는 6을 기준으로 다시 정렬한다.
• AVL 트리, 레드- 블랙 트리 같은 균형을 맞추는 다양한 알고리즘이 존재한다.
• 자바의 TreeSet은 레드-블랙 트리르 사용해서 균형을 지속해서 유지한다. 따라서, 최악의 경우에도 O(logN)의 성능을 제공한다.

이진 탐색 트리 - 순회

• 이진 탐색 트리의 핵심은 입력 순서가 아니라, 데이터의 값을 기준으로 정렬해서 보관한다는 점이다.
• 따라서 정렬된 순서로 데이터를 차례로 조회할 수 있다. (순회 할 수 있다.)
• 데이터를 차례로 순회하려면 중위 순회라는 방법을 사용하면 된다. 왼쪽 서브트리를 방문한 다음, 현재 노드를 처리하고, 마지막으로 오른쪽 서브트리를 방문한다. 이 방식은 이진 탐색 트리의 특성상, 노드를 오름차순(숫자가 점점 커짐)으로 방문한다.

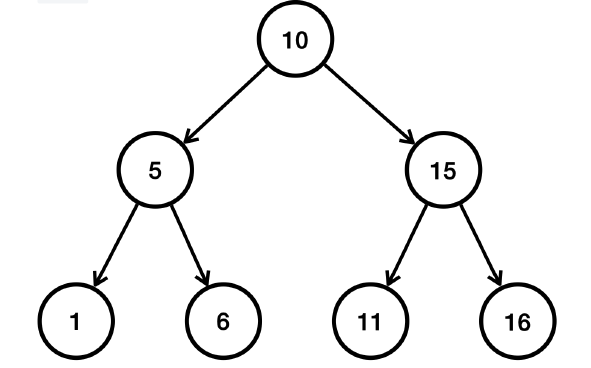
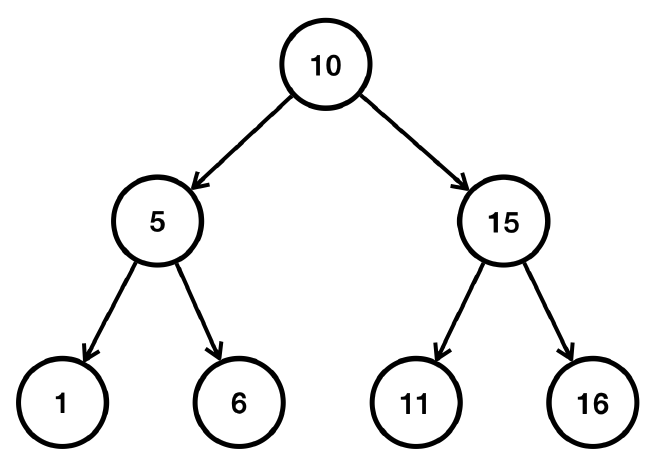
중위 순회 순서
중위 순회는 자신의 왼쪽의 모든 노드를 처리한 뒤, 자신의 노드를 처리하고, 자신의 오른쪽 모든 노드를 처리하는 방식이다.

• 10의 기준에서 왼쪽 서브트리를 방문한다.
  • 5의 기준에서 왼쪽 서브트리를 방문한다.
    • 1을 출력한다.
  • 5 자신을 출력한다.
  • 5의 기준으로 오른쪽 서브트리를 방문한다.
    • 6을 출력한다.
• 10 자신을 출력한다.
• 10의 기준에서 오른쪽 서브트리를 방문한다.
  • 15의 기준에서 왼쪽 서브트리를 방문한다.
    • 11을 출력한다.
  • 15 자신을 출력한다.
  • 15의 기준으로 오른쪽 서브트리를 방문한다.
    - 16을 출력한다.
    순서대로 1,5,6,10,11,15,16이 출력된 것을 확인할 수 있다.

3. 자바가 제공하는 Set3 - 예제

public class JavaSetMain {

    public static void main(String[] args) {
        run(new HashSet<>());
        run(new LinkedHashSet<>());
        run(new TreeSet<>());
    }

    private static void run(Set<String> set) {
        System.out.println("set = " + set.getClass());
        set.add("C");
        set.add("B");
        set.add("A");
        set.add("1");
        set.add("2");

        Iterator<String> iterator = set.iterator();
        while (iterator.hasNext()) {
            System.out.print(iterator.next() + " ");
        }
        System.out.println();
    }
}

• HashSet , LinkedHashSet , TreeSet 모두 Set 인터페이스를 구현하기 때문에 구현체를 변경하면서 실행할 수 있다.
• iterator() 를 호출하면 컬렉션을 반복해서 출력할 수 있다.
  • iterator.hasNext() : 다음 데이터가 있는지 확인한다.
  • iterator.next() : 다음 데이터를 반환한다.

실행 결과

set = class java.util.HashSet
A 1 B 2 C
set = class java.util.LinkedHashSet
C B A 1 2
set = class java.util.TreeSet
1 2 A B C

• HashSet : 입력한 순서를 보장하지 않는다.
• LinkedHashSet : 입력한 순서를 정확히 보장한다.
• TreeSet : 데이터 값을 기준으로 정렬한다.

4. 자바가 제공하는 Set4 - 최적화

자바 HashSet과 최적화

• 자바의 HashSet은 우리가 직접 구현한 내용과 거의 같지만 다음과 같은 최적화를 추가로 진행한다.

최적화

• 해시 기반 자료구조를 사용하는 경우 통계적으로 데이터의 수가 배열의 크기를 75% 정도 넘어가면 해시 인덱스가 자주 충돌한다. 따라서, 75%가 넘어가면 성능이 떨어지기 시작한다.
  • 해시 충돌로 같은 해시 인덱스에 들어간 데이터를 검색하려면 모두 탐색해야 한다. 따라서, 성능이 O(n) 으로 좋지 않다.
• 하지만 데이터가 동적으로 계속 추가되기 때문에 적절한 배열의 크기를 정하는 것은 어렵다.
• 자바의 HashSet은 데이터의 양이 배열 크기의 75%를 넘어가면 배열의 크기를 2배로 늘리고 2배 늘어난 크기를 기준으로 모든 요소에 해시 인덱스를 다시 적용한다.
  • 해시 인덱스를 다시 적용하는 시간이 걸리지만, 결과적으로 해시 충돌이 줄어든다.
• 자바의 HashSet의 기본 크기는 16이다.

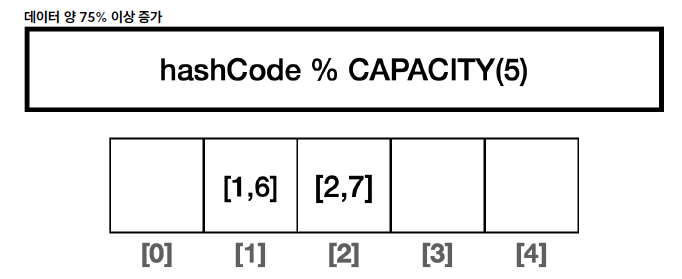
• CAPACITY는 5인데 4개가 있으므로 75% 이상 증가하였기 때문에 그 만큼 해시 인덱스의 충돌 가능성도 높아진다.

배열의 크기 2배 증가, 해시 다시 계산

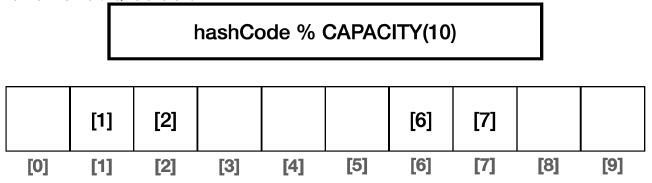
• 데이터의 양이 75% 이상이면 배열의 크기를 2배로 증가하고, 모든 데이터의 해시 인덱스를 커진 배열에 맞추어 다시 계산한다. 이 과정을 재해싱이라 한다.
• 인덱스 충돌 가능성이 줄어든다.
• 여기서 데이터가 다시 75% 이상 증가하면 다시 2배 증가와 재계산을 반복한다.

정리

Set 이 필요한 경우 HashSet 을 가장 많이 사용한다. 그리고 입력 순서 유지, 값 정렬의 필요에 따라서 LinkedHashSet, TreeSet 을 선택하면 된다.