[KT Aivle AI] 6주차. 딥러닝(3) 성능관리, Functional API

0. 개요 및 복습

주제 : 딥러닝
목표 : 머신러닝에서 나아가 딥러닝에 대해 배워 보자!

1) early stopping 코드

# 모델 선언
clear_session()

model2 = Sequential( [Dense(128, input_shape = (nfeatures,), activation= 'relu'),
                      Dense(64, activation= 'relu'),
                      Dense(32, activation= 'relu'),
                      Dense(1, activation= 'sigmoid')] )
model2.compile(optimizer= Adam(learning_rate = 0.001), loss='binary_crossentropy')

# EarlyStopping 설정 ------------
min_de = 0.001
pat = 5

es = EarlyStopping(monitor = 'val_loss', min_delta = min_de, patience = pat)
# --------------------------------

# 학습
hist = model2.fit(x_train, y_train, epochs = 100, validation_split=0.2,
                  callbacks = [es]).history
dl_history_plot(hist)

2) L1 규제

# 메모리 정리
clear_session()

# Sequential 타입
model4 = Sequential( [Dense(128, input_shape = (nfeatures,), activation= 'relu',
                            kernel_regularizer = l1(0.01)),
                      Dense(64, activation= 'relu',
                            kernel_regularizer = l1(0.01)),
                      Dense(32, activation= 'relu',
                            kernel_regularizer = l1(0.01)),
                      Dense(1, activation= 'sigmoid')] )

# 컴파일
model4.compile(optimizer= Adam(learning_rate = 0.001), loss='binary_crossentropy')

# 학습
hist = model4.fit(x_train, y_train, epochs = 100, validation_split=0.2, verbose = 0).history

# 학습결과 그래프
dl_history_plot(hist)

3) L3 규제

# 메모리 정리
clear_session()

# Sequential 타입
model5 = Sequential( [Dense(128, input_shape = (nfeatures,), activation= 'relu',
                            kernel_regularizer = l2(0.05)),
                      Dense(64, activation= 'relu',
                            kernel_regularizer = l2(0.05)),
                      Dense(32, activation= 'relu',
                            kernel_regularizer = l2(0.05)),
                      Dense(1, activation= 'sigmoid')] )

# 컴파일
model5.compile(optimizer= Adam(learning_rate = 0.001), loss='binary_crossentropy')

# 학습
hist = model5.fit(x_train, y_train, epochs = 100, validation_split=0.2, verbose = 0).history

# 학습결과 그래프
dl_history_plot(hist)

4) Dropout

# input_shape : feature 수 도출
nfeatures = x_train.shape[1]

# 메모리 정리
clear_session()

# Sequential 타입
model1 = Sequential( [Dense(128, input_shape = (nfeatures,), activation= 'relu'),
                      Dense(64, activation= 'relu'),
                      Dense(32, activation= 'relu'),
                      Dense(1, activation= 'sigmoid')] )

# 컴파일
model1.compile(optimizer= Adam(learning_rate = 0.001), loss='binary_crossentropy')

# 학습
hist = model1.fit(x_train, y_train, epochs = 100, validation_split=0.2, verbose = 0).history

# 학습결과 그래프
dl_history_plot(hist)

1. 성능관리

0) 과적합 방지하기

과적합은 왜 문제가 될까?

• 모델이 복잡해지면, 가짜 패턴까지 학습하게 된다.

무엇을 조절해서 '적절한 모델'을 만들 수 있을까?

• Epoch와 learning_rate
• 모델 구조 조정 : hidden layer, node 수
• Early Stopping
• Regularization(규제) : L1, L2
• Dropout

1) 과적합 방지하기 : Early Stopping

반복 학습 횟수가 많으면 과적합 될 수 있음

• 항상 과적합이 발생되는 것은 아님
• 그러나 반복 횟수가 증가할수록 오차 감소 -> 다시 증가할 수 있음
• 이를 방지하기 위한 방법 : Early Stopping

from keras.callbacks import EarlyStopping
es = EarlyStopping(monitor = 'val_loss', min_delta = 0, patience = 0)

EarlyStopping 옵션

• monitor : 기본값 val_loss
• min_delta : 오차의 최소값에서 변화량이 몇 이상 되어야 하는지 지정
• patience : 오차가 줄어들지 않는 상황을 몇 번 기다려줄 건지 지정

model.fit(x_train, y_train, epochs = 100, validation_split=0.2, callbacks = [es])

.fit안에 지정

• callbacks : epoch 단위로 학습이 진행되는 동안, 중간에 개입할 task 지정

2) 과적합 방지하기 : 가중치 규제 Regularization

오차함수에 페널티 추가 포함
1. L1규제 : Lasso

• 오차함수 = 오차 + λ∙σ|𝑤|
  • λ : 규제 강도
  • σ|𝑤| : 가중치(파라미터) 절대값의 합
• 효과 : 가중치 절대값의 합을 최소화 ➔ 가중치가 작은 값들은 0으로 만드는 경향

2. L2 규제 : Ridge
- 오차 함수 = 오차 + λ∙σ𝑤2
▪ 효과 : 가중치 제곱의 합을 최소화
➔ 규제 강도에 따라 가중치 영향력을 제어.
➔ 강도가 크면, 큰 가중치가 좀 더 줄어드는 효과, 작은 가중치는 0에 수렴

L1 규제와 L2 규제의 강도 : 일반적인 값의 범위

• L1규제 : 0.0001 ~ 0.1
• L2규제 : 0.001 ~ 0.4
• 강도가 높을수록 일반화된 모델

- 코드 : 은닉층 안에 옵션으로 지정

model4 = Sequential( [Dense(128, input_shape = (nfeatures,), activation= 'relu',
                            kernel_regularizer = l1(0.01)),
                      Dense(64, activation= 'relu',
                            kernel_regularizer = l1(0.01)),
                      Dense(32, activation= 'relu',
                            kernel_regularizer = l1(0.01)),
                      Dense(1, activation= 'sigmoid')] )

2. Functional API

1) Sequential API vs. Functional API

Sequential

• 순차적으로 쌓아가며 모델 생성
• input -> Ouput Layer로 순차적 연결

# 코드
clear_session()

model = Sequential([
            Dense(18 ,input_shape = (nfeatures, ),
                  activation = 'relu' ),
            Dense(4, activation='relu') ,
            Dense(1) ])

model.summary()

Functional

• 모델을 좀더 복잡하게 구성
• 모델을 분리해서 사용 가능
• 다중 입력, 다중 출력 가능

# 코드
clear_session()

il = Input(shape=(nfeatures, ))
hl1 = Dense(18, activation='relu')(il)
hl2 = Dense(4, activation='relu')(hl1)
ol = Dense(1)(hl2)

model = Model(inputs = il, outputs = ol)

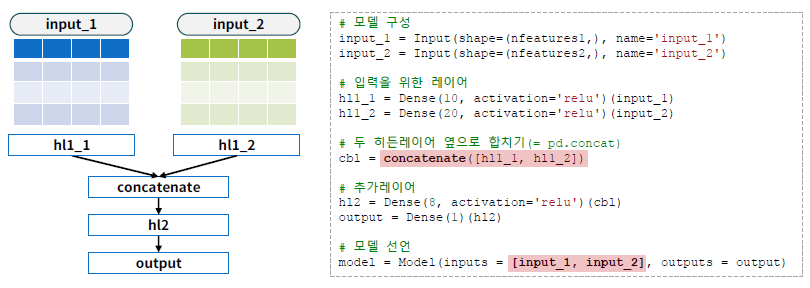
model.summary()

다중 입력 예제

• 카시트 판매 데이터를 두가지 입력으로 구분