[알고리즘] 그리디(Greedy)

그리디(Greedy) 알고리즘은 글로벌 최적을 찾기 위해 각 단계에서 로컬 최적의 선택을 하는 휴리스틱 문제 해결 알고리즘이다.

'greedy'라는 이름답게 그리디 알고리즘은 눈앞의 이익만을 좇는다.
대부분의 문제들은 로컬 최적해를 찾는 탐욕스러운 방법으로 잘 해결되지 않는다.
그러나 최적해를 찾는 것을 목표로 삼되, 찾기 어려운 경우에는 주어진 시간 내에 그런대로 괜찮은 해를 찾는다면 나름 합리적일 것이다.
이러한 측면에서 그리디 알고리즘은 합리적인 시간 내에 최적에 가까운 답을 찾을 수 있다는 점에서 유용하다.

탐욕 선택 속성 & 최적 부분 구조

그리디 알고리즘은 탐욕 선택 속성을 갖고 있는 최적 부분 구조 문제들에서 유용하다.

1. 탐욕 선택 속성이란, 앞의 선택이 이후 선택에 영향을 주지 않는 것을 의미한다.
2. 최적 부분 구조란, 최적 해결 방법이 부분 문제에 대한 최적 해결 방법으로 구성되는 경우를 말한다.

두 조건이 성립하지 않는 경우에는 그리디 알고리즘은 글로벌 최적해를 구하지 못한다.

하지만 그러한 경우에도 그리디 알고리즘은 근사 알고리즘으로 사용될 수 있으며, 대부분의 경우 계산 속도가 빠르기 때문에 실용적이다.
이 경우에도 최적해에 얼마나 가까운 해를 계산할 수 있는지를 보장하기 위한 증명이 필요하다.

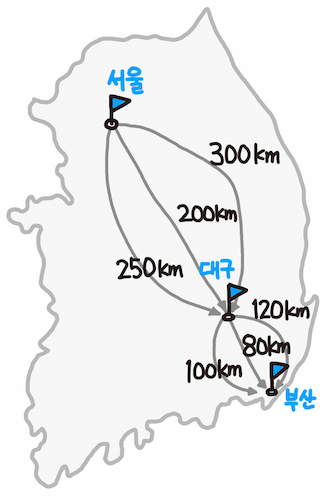
최적 부분 구조를 위 그림으로 더 자세히 설명할 수 있다.
서울에서 대구를 거쳐 부산까지 가는 최단 경로는, 각각의 부분 문제인 1)서울에서 대구까지 가는 최단 경로 문제, 2)대구에서 부산까지 가는 최단 경로 문제의 해결 방법의 합이다.
이처럼 문제의 최적 해결 방법은 부분 문제에 대한 최적 해결 방법으로 구성되는 구조를 최적 부분 구조라 한다.

결국 그리디 알고리즘은 각 단계마다 로컬 최적해를 찾는 문제로 접근해 문제를 점점 줄여나가는 형태로 문제를 해결한다.

그리디 알고리즘으로 해결할 수 있는 문제들에는 분할 가능 배낭 문제(Fractional Knapsack Problem), 동전 바꾸기 문제 등이 있다.