📌 CONCEPT.

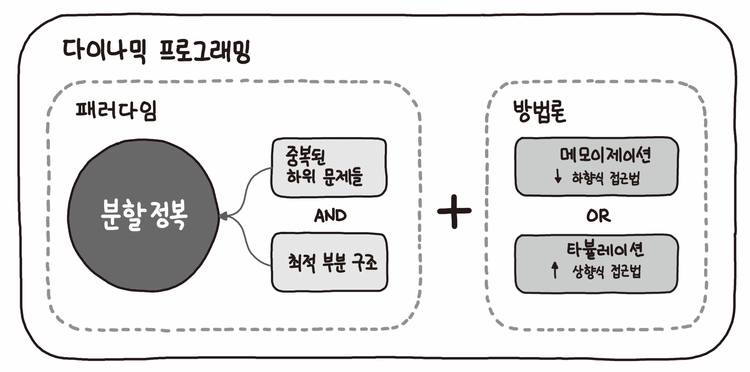
동적 계획법이란 문제를 작은 문제로 분할하여 해결한 결과를 저장해 나중에 큰 문제의 결과에 합하여 풀이하는 알고리즘으로,
최적 부분 구조를 띤, 즉 문제의 최적 해결 방법이 부분 문제에 대한 최적 해결 방법으로 이루어져 있는 문제를 풀이할 수 있는 방법이다.

EX. 피보나치 수열

def fib(n):
	if n <= 1:
    	return n
	return fib(n - 1) + fib(n - 2)

위는 피보나치 수열의 n번째 항을 구하는 함수이다.
fib(5)를 계산한다고 하자.

fib(5)
= fib(4) + fib(3)
= fib(3) + fib(2) + fib(2) + fib(1)
= fib(2) + fib(1) + fib(1) + fib(0) + fib(1) + fib(0) + fib(1)
= fib(1) + fib(0) + fib(1) + fib(1) + fib(0) + fib(1) + fib(0) + fib(1)

풀어서 쓴 계산식을 보면 같은 함수가 여러 번 반복됨을 알 수 있다.
fib(5)를 계산하기 위해 fib(4)와 fib(3)을 호출하는데, 이때 호출된 fib(4)에서 또 fib(3)이 호출되는 것처럼 말이다.
특히, n > 1이면 이미 계산한 적 있는 fib(n - 1) + fib(n - 2)를 중복해서 또 계산하게 되어 비효율적이다.

이러한 경우 동적 계획법을 이용해 중복되는 계산을 줄일 수 있다.

1. 상향식(Bottom-up)

def fib(n):
    dp[0] = 0
    dp[1] = 1
    
    for i in range(2, n + 1):
        dp[i] = dp[i - 1] + dp[i - 2]
    return dp[n]

상향식은 타뷸레이션(Tabulation)이라고도 하는데, 가장 작은 문제부터 시작해 작은 문제들을 점점 쌓아 큰 문제를 푸는 것이다.

fib(0)과 fib(1)을 해결하면 fib(2)를 해결할 수 있고, fib(1)과 fib(2)를 해결하면 fib(3)을 해결할 수 있고, fib(n - 2)와 fib(n - 1)을 해결하면 fib(n)을 해결할 수 있다.
수열의 점화식과 비슷한 것으로, 간혹 이 방식만을 동적 계획법으로 지칭하기도 한다.

2. 하향식(Top-down)

def fib(n):
	if n <= 1:
    	return n

    if not dp[n]:
        dp[n] = fib(n - 1) + fib(n - 2)
    return dp[n]

하향식은 메모이제이션(Memoization)이라고도 하는데, 가장 큰 문제부터 시작해서 작은 문제로 분할해 나가며 문제를 푸는 것이다.

하향식의 핵심은 계산한 것을 저장해두었다가 나중에 재활용한다는 점이다.
fib(k)를 처음 호출할 때 fib(k - 1) + fib(k - 2)를 계산해 dp[k]에 저장해놓고, 이후에 호출되는 fib(k)는 별다른 계산 없이 dp[k]를 가져다 쓰게 된다.

📌 최적 부분 구조

(다이나믹 프로그래밍, 그리디, 분할 정복)은 모두 최적 부분 구조 문제를 해결할 수 있는 알고리즘이라는 공통점이 있다.
이 세 알고리즘의 차이점은 아래와 같다.

알고리즘	풀이 가능한 문제들의 특징	풀이 가능한 문제 및 알고리즘
다이나믹 프로그래밍	- 최적 부분 구조 - 중복된 하위 문제들	- 0/1 배낭 문제 - 피보나치 수열 - 다익스트라 알고리즘
그리디 알고리즘	- 최적 부분 구조 - 탐욕 선택 속성	- 분할 가능 배낭 문제 - 다익스트라 알고리즘
분할 정복	- 최적 부분 구조	- 병합 정렬 - 퀵 정렬