[알고리즘] 병합 정렬(Merge Sort)

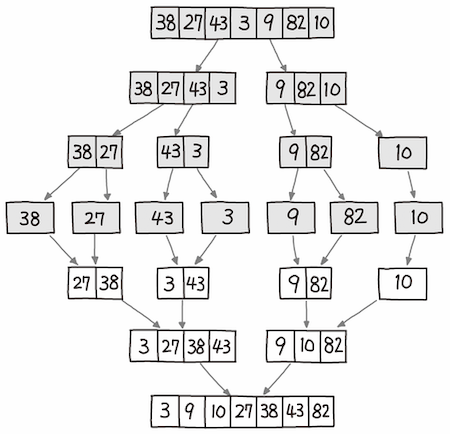
1. 모든 요소들을 가장 작은 단위의 리스트로 분할한다.
2. 인접한 리스트끼리 병합한다.
   병합할 때에는 두 리스트의 맨앞 요소들을 투 포인터로 비교하면서 계속해서 작은 값을 취한다.

특징

병합 정렬은 분할 정복(Divide and Conquer) 알고리즘 중 하나로, 어떠한 경우에도 O(N log N)이 소요된다.
이러한 일정한 실행 속도를 가지고 있다는 것이 병합 정렬의 장점이자 단점이다.
언제든 고른 성능을 보여주지만, 사실 대부분의 경우 퀵 정렬보다 느리기 때문이다.
물론 실무에서는 고른 성능을 위해 병합 정렬을 활발히 사용한다.

하지만 데이터 크기만큼의 메모리 공간을 더 필요로 한다는 단점 역시 존재한다.

구현 [Python]

def merge_sort(array: List[int]) -> List[int]:
    if len(array) == 1:
        return array
    mid = len(array) // 2
    a = merge_sort(array[:mid])
    b = merge_sort(array[mid:])

    merged, i, j = [], 0, 0
    while i < len(a) and j < len(b):
        if a[i] < b[j]:
            merged.append(a[i])
            i += 1
        else:
            merged.append(b[j])
            j += 1

    if i < len(a):
        merged.extend(a[i:])
    else:
        merged.extend(b[j:])

    return merged

아래는 병합하는 부분을 더 Pythonic하게 구현한 코드이다.

def merge_sort(array: List[int]) -> List[int]:
    if len(array) == 1:
        return array
    mid = len(array) // 2
    a = merge_sort(array[:mid])
    b = merge_sort(array[mid:])

    merged = []
    while a and b:
        if a[-1] > b[-1]:
            merged.append(a.pop())
        else:
            merged.append(b.pop())

    while a:
        merged.append(a.pop())
    while b:
        merged.append(b.pop())

    return merged[::-1]