- 배열의 i번째 인덱스에 있는 값인 key를 삽입하려고 한다.
- i - 1번째에서 시작해 왼쪽으로 가며 key가 삽입될 위치를 찾아 저장한다.
(이 과정이 종료될 시, 배열의 0번째부터 i번째까지 정렬되어 있게 된다.)- i + 1번째 인덱스에 대해 같은 동작을 수행한다.
특징
삽입 정렬은 그 원리와 구현이 매우 간단하다.
핵심 원리는 i번째 값을 삽입하려고 할 때, 0번째부터 i - 1번째까지는 정렬된 상태라는 점이다.
이는 매 사이클(pass)마다 값을 하나씩 정렬함으로써 알고리즘이 정상적으로 종료됨을 보장하기도 한다.
삽입 정렬은 O(N^2)의 시간 복잡도를 가지지만, 버블 정렬, 선택 정렬 등의 다른 O(N^2) 알고리즘보다 효율적이다.
비교 연산이 필요 없어지면 바로 멈추기 때문이다.
특히 대부분의 원소가 정렬되어 있는 경우, 비교 연산의 횟수가 상당히 줄어들어 O(N)에 가까운 비용이 소요된다.
삽입 정렬은 이진(Binary) 삽입 정렬로 파생되기도 하였다.
값이 삽입될 위치를 찾는 과정에서 이진 검색을 활용해 최적화한 것이다.
구현 [Python]
1.
삽입하려는 값 key의 자리를 찾을 때까지 배열을 오른쪽으로 밀어낸다.
key가 삽입될 인덱스를 찾으면 그곳에 key를 저장한다.
def insertion_sort(a: List[int]) -> None:
for i in range(1, len(a)):
key = a[i]
j = i - 1
while j >= 0 and key < a[j]:
a[j + 1] = a[j]
j -= 1
a[j + 1] = key2.
삽입하려는 값 key의 자리를 찾을 때까지 key의 왼쪽에 있는 값과 스왑 연산을 수행한다.
key가 삽입될 인덱스에 도착하면 스왑 연산을 멈춘다.
def insertion_sort(a: List[int]) -> None:
for i in range(1, len(a)):
j = i
while j > 0 and a[j - 1] > a[j]:
a[j - 1], a[j] = a[j], a[j - 1]
j -= 1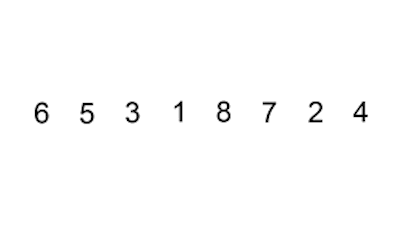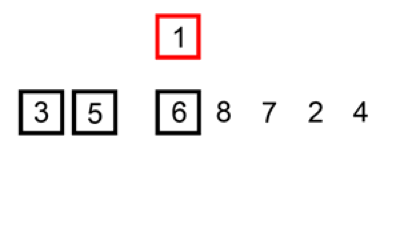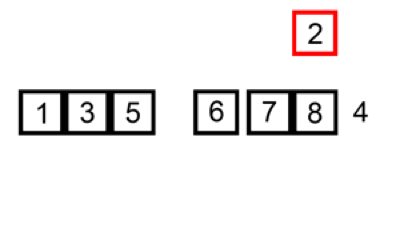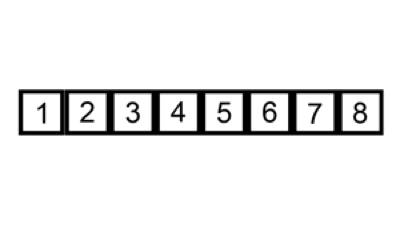
참고 자료 :
https://en.wikipedia.org/wiki/Insertion_sort
https://namu.wiki/w/정렬%20알고리즘#s-2.1.3