그래프 순회(Graph Traversal)란, 그래프의 정점들을 방문 또는 검색하는 동작을 일컫는다.

크게 두 가지 방식으로 아래 그래프를 순회해보도록 하자.
해당 유향 그래프는 인접 리스트로 구현하였다.

graph = {
    1: [],
    3: [1, 6],
    4: [],
    6: [4, 7],
    7: [],
    8: [3, 10],
    10: [14],
    13: [],
    14: [13]
}

---

DFS(Depth First Search)

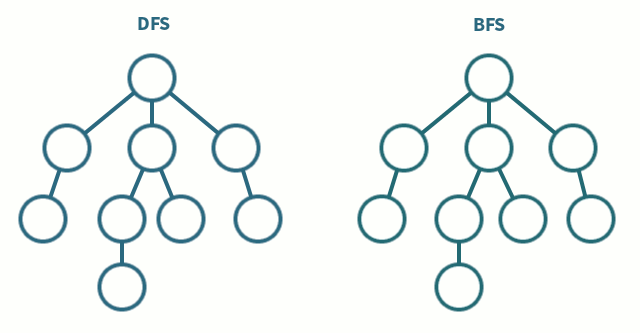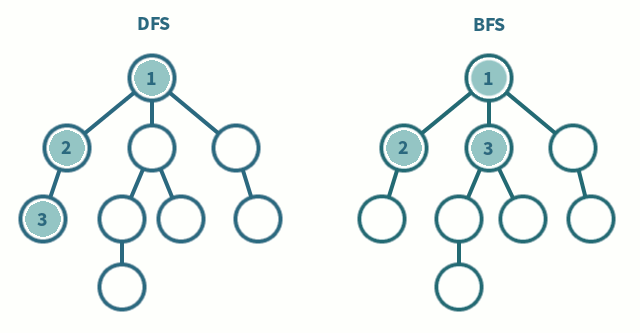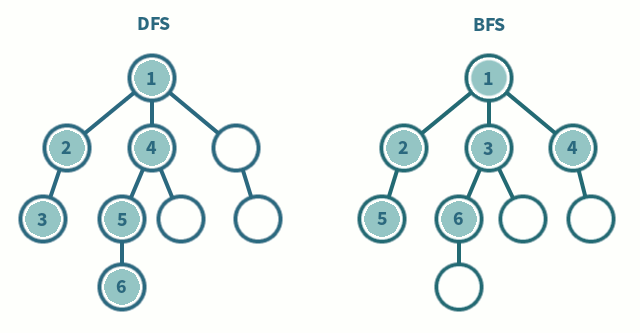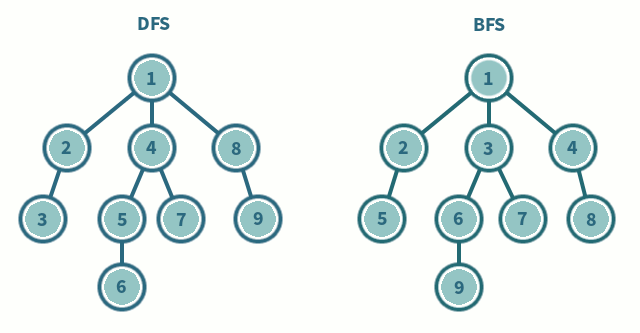
깊이 우선 탐색(DFS - Depth First Seach)은 그래프에서 가장 깊은 정점들을 차례로 탐색하는 방식이다.

연결된 정점이 더 없을 때까지 계속해서 다음 정점을 탐색하다가, 가장 깊은 정점에 도달하게 되었을 때, 가장 최근에 만났던 갈림길로 돌아가 같은 작업을 반복한다.

DFS는 스택이나 재귀로 구현한다.

구현 [Python]

def dfs(start: int) -> list:
    discovered = []
    stack = [start]
    while stack:
        if (v := stack.pop()) not in discovered:
        	discovered.append(v)
        	for next_vertex in graph[v]:
            	stack.append(next_vertex)
    return discovered


print(dfs(8))  # [8, 10, 14, 13, 3, 6, 7, 4, 1]

def dfs(v: int, discovered=[]) -> list:
    discovered.append(v)
    for next_vertex in graph[v]:
    	if next_vertex not in discovered:
        	discovered = dfs(next_vertex, discovered)
    return discovered


print(dfs(8))  # [8, 3, 1, 6, 4, 7, 10, 14, 13]

위에서부터 차례로 스택, 재귀를 이용해 DFS를 구현하였다.
우리가 다루고 있는 그래프에서는 필요하지 않지만, 한 정점을 중복해서 방문하지 않기 위해 다음 정점이 discovered에 존재하는지를 검사하게 되어 있다.

만약 1에서 4로 가는 간선이 존재했다면, 정점 4는 1→4, 6→4로 중복해서 방문된다.

---

BFS(Breadth First Search)

너비 우선 탐색(BFS - Breadth First Search)은 탐색 중인 정점에 인접한 정점들을 차례로 탐색하는 방식이다.

시작 정점으로부터 가까운 정점들부터 탐색하는 방식으로, 탐색할 정점들을 물둘레 퍼지듯 넓혀간다.

BFS는 최단 경로를 찾을 때 유용하며, 큐로 구현된다.

구현 [Python]

def bfs(start: int) -> list:
    discovered = [start]
    queue = [start]
    while queue:
        for next_vertex in graph[queue.pop(0)]:
            if next_vertex not in discovered:
                discovered.append(next_vertex)
                queue.append(next_vertex)
    return discovered


print(bfs(8))  # [8, 3, 10, 1, 6, 14, 4, 7, 13]