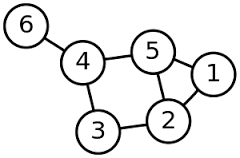
그래프(Graph)란, 일부 쌍들이 연관되어 있는 객체 집합 구조로, 객체 간에 짝을 이루는 관계를 모델링하기 위해 사용된다.
정점(vertex)과 간선(edge)을 이용해 그 관계를 나타낸다.

그래프를 구현하는 방식에는 두 가지 방법이 있다.

인접 행렬(Adjacent Matrix)

정점의 개수를 N이라고 할 때, N x N 행렬 adj_mat를 만든다.
adj_mat[i][j]는 정점 i와 정점 j의 인접 여부를 나타낸다.
무향 그래프의 경우, 인접 행렬은 대칭이라는 사실 역시 알 수 있다.

• 장점 및 단점
  두 정점의 인접 여부를 확인할 때 O(1)에 접근할 수 있어 용이하다.
  그러나 정점 v에 인접한 다른 정점들을 모두 찾고자 하는 경우, adj_mat[v][1] ~ adj_mat[v][N]을 확인하므로 O(N)이 걸린다.
  N x N 배열을 꼭 선언해야 하므로 메모리가 낭비될 가능성도 높다.

구현 [Python]

V = 6  # of vertices.
E = 6  # of edges.
adj_mat = [[0] * V for _ in range(V)]

for _ in range(E):
    v1, v2 = map(int, input().split())
    adj_mat[v1 - 1][v2 - 1] = 1
    adj_mat[v2 - 1][v1 - 1] = 1

for row in adj_mat:
    print(row)

input :
1 2
2 3
2 5
3 4
4 5
4 6

output :
[0, 1, 0, 0, 0, 0]
[1, 0, 1, 0, 1, 0]
[0, 1, 0, 1, 0, 0]
[0, 0, 1, 0, 1, 1]
[0, 1, 0, 1, 0, 0]
[0, 0, 0, 1, 0, 0]

인접 리스트(Adjacent List)

정점의 개수를 N이라고 할 때, N개의 빈 리스트를 담은 이중 리스트 adj_list를 만든다.
adj_list[i]는 정점 i와 인접한 정점들의 리스트이다.

• 장점 및 단점
  연결된 정점들의 관계만 저장하므로 메모리가 낭비되지 않는다.
  정점 v에 인접한 다른 정점들을 모두 찾고자 하는 경우, adj_list[i]만 확인하면 되므로 O(K)가 걸린다.
  그러나 두 정점 v1과 v2의 인접 여부를 확인할 때 역시, adj_list[v1]의 원소를 다 확인하므로 O(K)가 걸린다.

구현 [Python]

import collections

V = 6  # of vertices.
E = 6  # of edges.
adj_list = collections.defaultdict(list)

for _ in range(E):
    v1, v2 = map(int, input().split())
    adj_list[v1].append(v2)
    adj_list[v2].append(v1)

for key, value in sorted(adj_list.items()):
    print('{} : {}'.format(key, value))

input :
1 2
2 3
2 5
3 4
4 5
4 6

output :
1 : [2]
2 : [1, 3, 5]
3 : [2, 4]
4 : [3, 5, 6]
5 : [2, 4]
6 : [4]

- 인접 행렬 vs 인접 리스트

두 정점의 인접 여부 확인                     --->  인접 행렬
한 정점에 인접한 정점들을 모두 검색   --->  인접 리스트
효율적 메모리 관리                              --->  인접 리스트

위에서도 앞서 살펴봤듯, 인접 행렬과 인접 리스트는 서로의 장점과 단점을 trade-off 한다.
따라서 상황에 맞는 적절한 방식을 택해 그래프를 구현해야 한다.