[자료구조] 이진 탐색 트리(BST - Binary Search Tree)

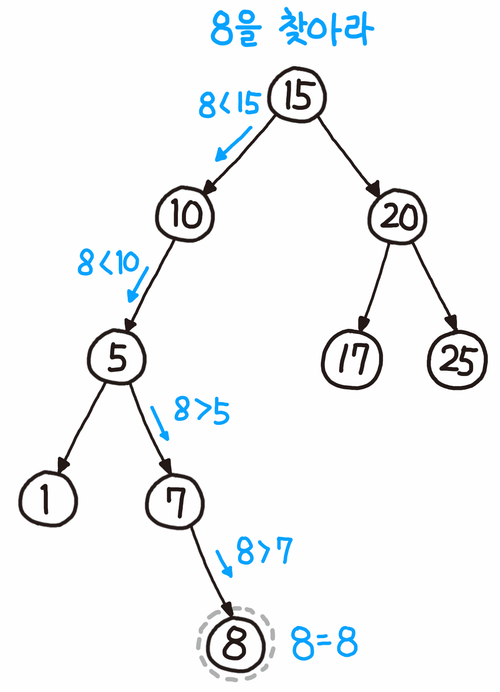
이진 탐색 트리(BST - Binary Search Tree)는 노드의 왼쪽, 오른쪽이 값의 크기에 따라 정렬되어 있는 트리이다.

노드의 왼쪽 서브트리에는 기준 노드보다 값이 작은 노드들이, 오른쪽 서브트리에는 기준 노드보다 값이 큰 노드들이 존재한다.

탐색하려는 값 x가 기준 노드의 값보다 작으면 기준 노드의 왼쪽 자식, 그렇지 않으면 기준 노드의 오른쪽 자식을 탐색한다.
이 작업을 루트 노드부터 시작해, 노드가 더 이상 존재하지 않거나 n을 발견할 때까지 진행하면 된다.

---

구현 [Python]

class Node:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

root = None

def search(x: int) -> bool:
    node = root
    while node:
        if x < node.val:
            node = node.left
        elif x > node.val:
            node = node.right
        else:
            return True
    return False

def insert(x: int) -> None:
    global root
    if root is None:
        root = Node(x)
        return

    prev = root
    while True:
        if x < prev.val:
            if prev.left:
                prev = prev.left
            else:
                prev.left = Node(x)
                break
        else:
            if prev.right:
                prev = prev.right
            else:
                prev.right = Node(x)
                break

def delete(x: int) -> None:
    global root
    if root is None:
        return

    # find the node to delete.
    prev, cur = None, root
    while cur:
        if x < cur.val:
            prev, cur = cur, cur.left
        elif x > cur.val:
            prev, cur = cur, cur.right
        else:
            break
    else:
        return  # x is not in BST.

    # x has no child.
    if cur.left is None and cur.right is None:
        if prev is None:
            root = None
        elif x < prev.val:
            prev.left = None
        else:
            prev.right = None

    # x has only left child.
    elif cur.right is None:
        if prev is None:
            root = cur.left
        elif x < prev.val:
            prev.left = cur.left
        else:
            prev.right = cur.left

    # x has only right child.
    elif cur.left is None:
        if prev is None:
            root = cur.right
        elif x < prev.val:
            prev.left = cur.right
        else:
            prev.right = cur.right

    # x has two children.
    else:
        t, p = None, cur.right  # (trailing pointer, predecessor)
        while p.left:
            t, p = p, p.left

        if prev is None:
            root = p
        elif x < prev.val:
            prev.left = p
        else:
            prev.right = p

        if t is None:
            p.left = cur.left
        else:
            t.left = p.right
            p.left, p.right = cur.left, cur.right

탐색/삽입 구현은 어렵지 않으나, 삭제의 경우 케이스를 잘 분류해야 한다.
삭제하려는 노드가 자식 노드를 몇 개, 어디에 갖고 있는지 잘 따져야 한다.
특히, 삭제하려는 노드의 자식 노드가 두 개인 경우 적절한 전임자(predecessor)를 찾아 대체하는 것이 좋은 방법이다.

아래와 같이 데이터를 삽입할 수 있으며, print_tree 함수를 구현해 BST를 적당히 출력하면서 연산의 결과를 확인해볼 수 있다.

data = [50, 20, 80, 10, 30, 25, 35, 34, 32, 33, 40, 80, 90, 95, 85, 87]
for num in data:
    insert(num)

def print_tree():
    def preorder(node: Node) -> None:
        if node is None:
            return
        preorder(node.left)
        print(node.val, end=' ')
        preorder(node.right)

    if root:
        print('[', end=' ')
        preorder(root)
        print(']')  # br
    else:
        print('BST is empty.')

print_tree()
search(90)
delete(90); print_tree()
search(90)
delete(10); print_tree()
delete(80); print_tree()
delete(30); print_tree()
delete(32); print_tree()
delete(25); print_tree()
delete(40); print_tree()
delete(50); print_tree()
print(root.val)

output :
[ 10 20 25 30 32 33 34 35 40 50 80 80 85 87 90 95 ]
'90' is found.
[ 10 20 25 30 32 33 34 35 40 50 80 80 85 87 95 ]
'90' is not found.
[ 20 25 30 32 33 34 35 40 50 80 80 85 87 95 ]
[ 20 25 30 32 33 34 35 40 50 80 85 87 95 ]
[ 20 25 32 33 34 35 40 50 80 85 87 95 ]
[ 20 25 33 34 35 40 50 80 85 87 95 ]
[ 20 33 34 35 40 50 80 85 87 95 ]
[ 20 33 34 35 50 80 85 87 95 ]
[ 20 33 34 35 80 85 87 95 ]
80

구현을 하다 보면, 이진 검색(Binary Search)과 구현 원리의 전체적인 틀은 유사함을 알 수 있다.
이진 탐색 트리는 정렬된 구조를 유지하며 값을 저장 및 탐색할 수 있는 '자료구조'라면, 이진 검색은 정렬된 배열에서 값을 탐색할 수 있는 '알고리즘'이라고 할 수 있겠다.

---

높이 균형 문제

균형이 좋은 트리에서, 삽입/삭제/탐색에 O(log N)이 소요된다.
(삽입/삭제도 결국 탐색을 기반으로 하기 때문이다.)

좋은 높이 균형을 유지하기 위해서는, 트리의 높이를 최대한 낮게 하는 것이 좋다.

이진 탐색 트리는 균형이 좋게 만들어지는 경우가 많다.
그러나 운 나쁘게 균형이 많이 깨진 트리가 형성될 경우, 탐색 시 O(N)에 가까운 시간이 소요될 수 있으며, 강력한 로그 계산을 기반으로 하는 이진 탐색 트리의 장점을 전혀 살릴 수 없게 된다.

자가 균형 이진 탐색 트리(Self-Balancing BST)

자가 균형 이진 탐색 트리(Self-Balancing BST)는 스스로 높이 균형을 맞추는 이진 탐색 트리로, 최악의 경우에도 탐색에 O(log N)가 소요된다.
위에서 살펴본 높이 균형 문제를 해결하기 위해 고안된 것으로, AVL 트리(Adelson-Velsky and Landis Tree), 레드-블랙 트리(Red-black Tree) 등이 이에 속한다.

참고로, Java의 HashMap은 해시 테이블을 개별 체이닝으로 구현하면서도 연결 리스트와 함께 레드-블랙 트리를 병행해 저장함으로써 효율성을 갖추었다.