[자료구조] 트리 순회(Tree Traversal)

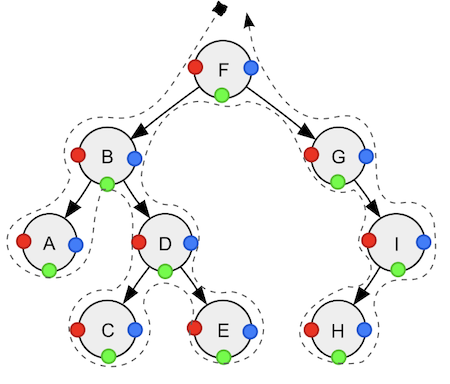
트리 순회란 그래프 순회의 한 형태로, 트리 자료구조에서 각 노드를 정확히 한 번 방문하는 과정을 일컫는다.

그래프와 마찬가지로 트리 역시 DFS 또는 BFS로 탐색하는데, 특히 이진 트리에서 DFS는 노드의 방문 순서에 따라 3가지 방식으로 구분된다.

전위(preorder) 순회 = NLR
중위(inorder) 순회 = LNR
후위(postorder) 순회 = LRN

전위, 중위, 후위 순회의 기준은 N의 방문 순서가 된다.
N은 현재 노드, L은 왼쪽 서브트리, R은 오른쪽 서브트리를 의미한다.

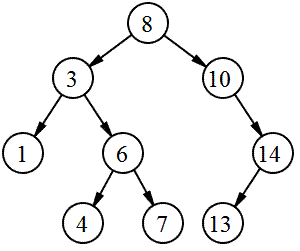
위의 트리를 각 방법으로 순회했을 때 결과는 다음과 같다.

preorder : 8 3 1 6 4 7 10 14 13
inorder : 1 3 4 6 7 8 10 13 14
postorder : 1 4 7 6 3 13 14 10 8

루트인 8의 방문 위치를 기준으로 왼쪽 서브트리, 오른쪽 서브트리의 방문 순서를 살펴볼 수 있다.

---

구현 [Python]

class TreeNode:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

트리 순회는 재귀를 이용해 쉽게 구현할 수 있다.

def preorder(node: Node) -> None:
    if node is None:
        return
    print(node.val, end=' ')
    preorder(node.left)
    preorder(node.right)

def inorder(node: Node) -> None:
    if node is None:
        return
    inorder(node.left)
    print(node.val, end=' ')
    inorder(node.right)

def postorder(node: Node) -> None:
    if node is None:
        return
    postorder(node.left)
    postorder(node.right)
    print(node.val, end=' ')

---

트리 복원

preorder, inorder, postorder의 세 가지 순회의 결과 중 두 개만 주어지면 순회한 이진 트리를 만들 수 있다.
(단, preorder와 postorder가 주어지는 경우에는 정(Full) 이진 트리일 때만, 즉 모든 노드의 자식 노드 개수가 0개 또는 2개일 때에만 복원 가능하다.)

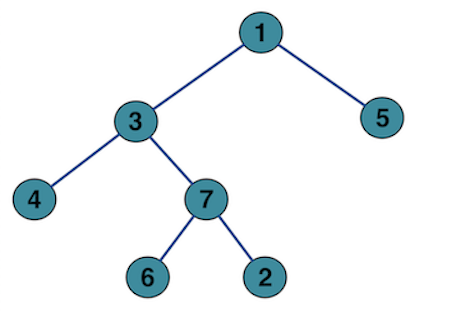
preorder = [1, 3, 4, 7, 6, 2, 5]
inorder = [4, 3, 6, 7, 2, 1, 5]
postorder = [4, 6, 2, 7, 3, 5, 1]

위 순회 결과를 갖고 트리를 복원해보도록 하자.

- preorder & inorder

preorder의 맨앞으로부터 항상 루트를 구할 수 있다.
따라서 루트를 기준으로 inorder를 4 3 6 7 2와 5로 구분할 수 있으며, 각각 왼쪽 서브트리와 오른쪽 서브트리가 된다.

1을 제외한 preorder의 맨앞으로부터 루트 3을 구할 수 있다.
왼쪽 서브트리를 4와 6 7 2로 구분할 수 있으며, 각각 왼쪽 서브트리와 오른쪽 서브트리가 된다.

(중략)

1 3 4 7 6 2를 제외한 preorder의 맨앞으로부터 루트 5를 구할 수 있다.
오른쪽 서브트리 5를 완성한다.

def build_tree(preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
    if inorder:
        node = TreeNode(preorder.pop(0))
        idx = inorder.index(node.val)
        node.left = build_tree(preorder, inorder[:idx])
        node.right = build_tree(preorder, inorder[idx + 1:])
        return node

- inorder & postorder

preorder에서 맨앞에서 루트를 얻었다면, postorder에서는 맨뒤에서 루트를 얻을 수 있다.
이하 원리는 preorder & inorder와 동일하다.

단, inorder와 함께 preorder가 주어지는 경우 왼쪽 서브트리가, postorder가 주어지는 경우 오른쪽 서브트리가 먼저 복원됨에 주의한다.
각각의 순회 순서 NLR, LRN에서 그 이유를 발견할 수 있다.

def build_tree(inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
    if inorder:
        node = TreeNode(postorder.pop())
        idx = inorder.index(node.val)
        node.right = build_tree(inorder[idx + 1:], postorder)
        node.left = build_tree(inorder[:idx], postorder)
        return node

- preorder & postorder

위에서 언급했듯, preorder와 postorder가 주어질 때에는 정 이진 트리만 복원할 수 있음에 주의한다.