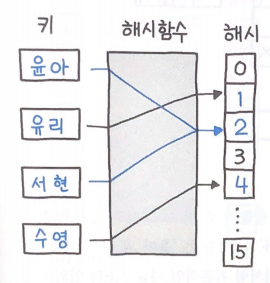
해시 테이블(Hash Table) 또는 해시 맵(Hash Map)은, 키를 값에 매핑(Key: Value)할 수 있는 구조인, 연관 배열(Associative Array)을 구현하는 자료구조이다.

---

해시 함수(Hash Function)

해시 테이블의 핵심은 해시 함수이다.
해시 함수란 '임의 크기 데이터'를 '고정 크기 값'으로 매핑하는 데 사용할 수 있는 단방향 함수이다.
이때 전자에 해당하는 입력 데이터를 키, 후자에 해당하는 매핑된 값을 해시 또는 해시 값이라고 한다.
다시 말해 해시 함수는 키를 해시 값으로 인코딩하는 함수라고 할 수 있다.

가령 ABC, 1324BC, AF32B라는 각각 길이가 3, 6, 5라는 문자열 키가 있다고 할 때, 각 문자열을 특정 해시 함수를 통과시켜 각각 A1, CB, D5, 즉 길이가 2인 문자열 해시 값에 매핑할 수 있다.

이러한 특징들 덕분에 잘 구현된 해시 테이블에서 데이터를 평균적으로 O(1)에 조회/삽입/삭제할 수 있게 된다.

해시 함수에서 키 값이 조금만 변해도 해시 값이 크게 달라지는데, 이를 암호학에서는 눈사태 효과(Avalanche Effect)라고 일컫는다.

해시 함수는 체크섬(Checksum), 손실 압축, 무작위화 함수(Randomization Function), 암호 등과도 관련이 깊으며 때로는 서로 혼용되기도 한다.

해싱(Hashing)

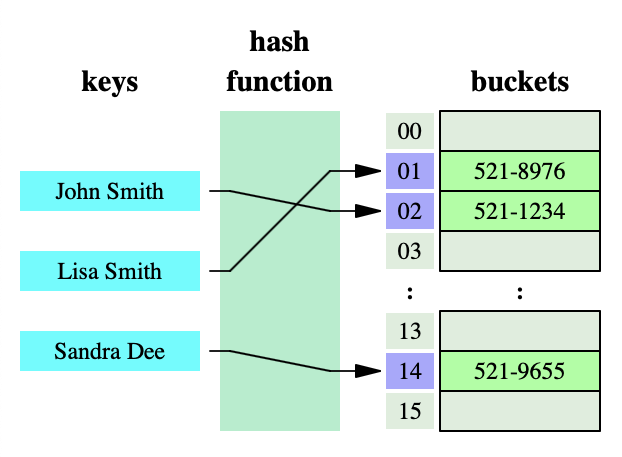
위 그림은 해시 함수를 통해 키가 해시 값으로 변환되는 과정을 도식화한 것으로, 이처럼 해시 함수를 적용해 해시 테이블을 인덱싱하는 작업을 해싱이라고 한다.

가장 단순하면서도 널리 쓰이는 것은 정수형 해싱 기법인 모듈로 연산을 이용한 나눗셈 방식이다.

h(x)는 해시 함수로, 입력값 x에 해시 함수를 적용해 생성된 결과를 뜻하며, m은 해시 테이블의 크기이다.
m은 일반적으로 충돌 문제를 위해 2의 멱수에 가깝지 않은 소수를 택하는 것이 좋다.

좋은 해시 함수의 특징

• 해시 값 충돌의 최소화
• 해시 테이블 전체에 해시 값이 균일하게 분포
• 쉽고 빠른 연산
• 해시 테이블 사용 효율이 높음
• 사용할 키의 모든 정보를 이용하여 해싱

---

해시 충돌(Hash Collision)

해시 충돌이란, 해시 함수가 서로 다른 두 입력값에 대해 동일한 출력값을 내는 상황을 의미한다.
해시 함수가 무한한 입력 데이터로부터 유한한 출력 데이터를 생성하는 경우, 비둘기 집 원리에 의해 해시 충돌 문제는 피할 수 없다.

비둘기집 원리(Pigeonhole Principle)

비둘기집 원리란, n개의 아이템을 m개의 컨테이너 넣을 때, n > m이라면 적어도 하나의 컨테이너에는 반드시 2개 이상의 아이템이 들어 있다는 원리를 말한다.

생일 문제(Birthday Problem)

해시 함수에서 충돌은 생각보다 쉽게 일어난다.
흔한 예로 생일 문제를 들 수 있다.
생일의 가짓수는 윤년을 제외하면 365개이므로, 여러 사람이 모였을 때 생일이 같은 2명이 존재할 확률은 꽤 낮을 것 같다.
하지만 실제로는 23명만 모여도 그 확률은 50%를 넘고, 57명이 모이면 99%를 넘어선다.
Python을 활용한 간단한 실험을 통해 어렵지 않게 이를 증명할 수 있다.
(참고로 이와 같이 컴퓨터 실험 통한 증명 방법은 1976년 4색 정리가 최초이다.)

import random

TRAILS = 100000
same_birthdays = 0

for _ in range(TRAILS):
    birthdays = []
    for _ in range(23):
        birthday = random.randint(1, 365)
        if birthday in birthdays:
            same_birthdays += 1
            break
        birthdays.append(birthday)

print(f'{same_birthdays / TRAILS * 100}%')

23명의 생일을 비교했을 때 생일이 같은 사람이 있는지 검사하는 것이 한 시행이며, 이러한 시행을 TRAILS번 반복한다.
실행 시 50%~51% 정도의 결과를 출력하는 것을 볼 수 있다.

로드 팩터(Load Factor)

로드 팩터란, 해시 테이블에 저장된 데이터 개수 n을 버킷의 개수 k로 나눈 것이다.
따라서 1이면 해시 테이블이 꽉 찬 것이고, 1보다 큰 경우 해시 충돌이 발생했음을 의미한다.
일반적으로 로드 팩터가 증가할수록 해시 테이블의 성능은 감소한다.

로드 팩터 비율에 따라서 해시 함수를 재작성해야 할지, 해시 테이블의 크기를 조정해야 할지 결정할 수 있다.

또한 이 값은 해시 함수가 키들을 잘 분산해주는지를 말하는 효율성 측정에도 사용된다.
가령 Java 10에서는 HashMap의 디폴트 로드 팩터를 0.75로 정했으며, '시간과 공간 비용의 적절한 절충안'이라고 말한다.
로드 팩터가 0.75를 넘어설 경우 동적 배열처럼 해시 테이블의 공간을 재할당하게 된다.

---

해시 테이블 구현

그렇다면 해시 충돌을 해결하여 해시 테이블을 구현하는 방법에는 어떤 것이 있을까?
해시 테이블의 인덱스 2에서 충돌이 났다고 가정해보자.

- 개별 체이닝(Separate Chaining)

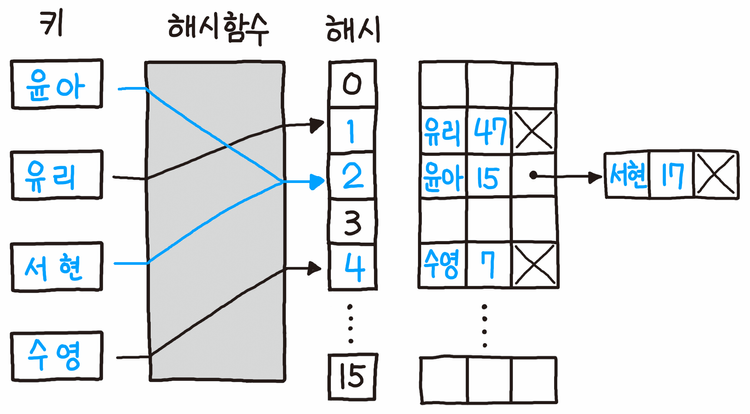
해시 테이블의 기본 방식이기도 한 개별 체이닝은 충돌 발생 시 연결 리스트(Linked List)로 연결하는 방식이다.
위 그림에서 인덱스 2에서 '윤아'에 충돌한 '서현'은 '윤아'의 다음 아이템으로 연결되었다.
전통적으로 흔히 해시 테이블이라고 하면 이 방식을 떠올리게 된다.

개별 체이닝의 간단한 원리를 요약하면 다음과 같다.

1. 키의 해시 값 계산
2. 해시 값을 이용해 배열의 인덱스 계산
3. 충돌 시 연결 리스트로 연결

구현 [Python]

class Node:
    def __init__(self, item: int, link=None):
        self.item = item
        self.link = link

class HashTable:
    def __init__(self):
        self.size = 3
        self.table = [None] * self.size

    def print_table(self) -> None:
        for i, root in enumerate(self.table):
            items = []
            while root:
                items.append(root.item)
                root = root.link
            print(i, end=' : ')
            print('->'.join(map(str, items)))

    def add(self, item: int) -> None:
        if self.table[item % self.size] is None:
            self.table[item % self.size] = Node(item)
            return
        prev = self.table[item % self.size]
        while prev.link:
            prev = prev.link
        prev.link = Node(item)

    def remove(self, item: int) -> None:
        if self.table[item % self.size] is None:
            return
        prev = self.table[item % self.size]
        while prev.link:
            if prev.link.item == item:
                prev.link = prev.link.link
                break

ht = HashTable()
for i in range(10 + 1):
    ht.add(i)
ht.print_table()

output:
0 : 0->3->6->9
1 : 1->4->7->10
2 : 2->5->8

- 오픈 어드레싱(Open Addressing)

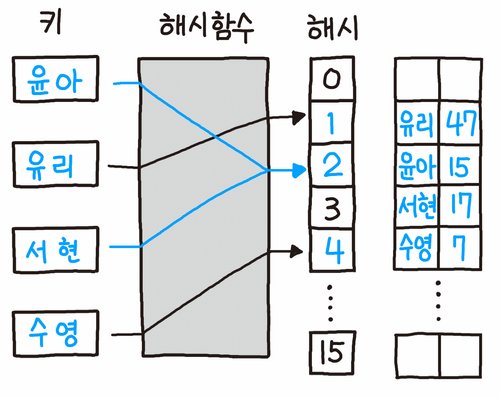
오픈 어드레싱은 충돌 발생 시 탐사(Probing)를 통해 다른 빈 공간을 찾아나서는 방식이다.
따라서 모든 원소가 반드시 자신의 해시 값에 대응하는 주소에 저장된다는 보장이 없다.
위 그림에서 '윤아'에 충돌한 '서현'은 빈 공간을 탐사해 인덱스 3에 저장되었다.

사실상 데이터를 무한정 저장할 수 있는 체이닝 방식과는 달리, 오픈 어드레싱은 전체 슬롯의 개수 이상 저장할 수 없다.

따라서 일정 로드 팩터 비율을 넘어서게 되면, 그로스 팩터(Growth Factor)에 따라 더 큰 크기의 버킷을 생성한 후 여기에 새롭게 복사하는 리해싱(Rehashing)이 일어난다.

선형 탐사(Linear Probing)

여러 가지 오픈 어드레싱 방식 중 가장 간단한 방식인 선형 탐사 방식은, 충돌이 발생할 경우 해당 위치부터 순차적으로 다음 위치를 확인하다가 빈 공간을 발견하면 그 자리에 데이터를 삽입한다.
선형 탐사 방식은 구현이 간단하면서도 전체적인 성능이 좋은 편이다.

그러나 선형 탐사 활용 시, 해시 테이블에 저장되는 데이터들이 고르게 분포되지 않고 뭉치는 경향이 있다.
해시 테이블 여기저기에 연속된 데이터 그룹이 생기는 이러한현상을 클러스터링(Clustering)이라고 하는데, 클러스터들이 점점 커지면 주변 클러스터들과 서로 합쳐지기도 한다.
그렇게 되면 해시 테이블 특정 위치에 데이터가 몰리게 되고, 이는 탐사 시간을 오래 걸리게 하여 해싱 효율을 떨어뜨린다.

구현 [Python]

class HashTable:
    def __init__(self):
        self.size = 3
        self.table = [None] * self.size

    def _probe(self, item: int, step: int) -> int:
        index = item % self.size
        while index < self.size:
            if self.table[index] is None:
                return index
            index += step
        return -1

    def print_table(self) -> None:
        for i, item in enumerate(self.table):
            print("{} : {}".format(i, item))

    def add(self, item: int) -> None:
        index = self._probe(item, 1)
        if index == -1:
            index = self._probe(item, -1)
        if index == -1:
            return
        self.table[index] = item

    def remove(self, item: int) -> None:
        start = item % self.size
        for i in range(start, self.size):
            if self.table[i] == item:
                self.table[i] = None
        for i in range(0, start):
            if self.table[i] == item:
                self.table[i] = None

ht = HashTable()
ht.add(1)
ht.add(4)
ht.add(2)
ht.print_table()

output:
0 : 2
1 : 1
2 : 4

언어별 해시 테이블 구현 방식

Python의 경우 오픈 어드레싱 방식으로 해시 테이블을 구현하였다.
CPython 구현부에는 "체이닝 시 malloc으로 메모리를 할당하는 오버헤드가 높아 오픈 어드레싱을 택했다."라는 주석이 적혀 있다.

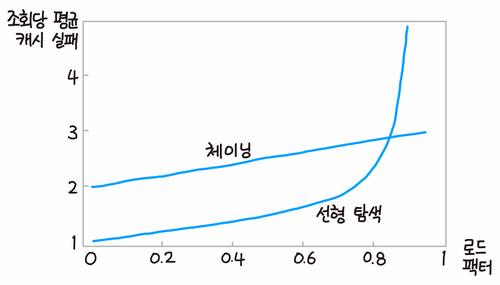
위 그래프에서 볼 수 있듯, 선형 탐사 방식은 해시 테이블이 80% 이상 차게 되면, 즉 로드 팩터가 0.8 이상이 되면 급격한 성능 저하를 발생시킨다.
앞서 언급했듯 개별 체이닝과는 달리, 로드 팩터 1 이상은 저장할 수 없기도 하다.
해시 테이블의 공간이 찰수록 탐사에 점점 더 오랜 시간이 걸리며, 가득 차게 될 경우 빈 공간을 찾을 수 없기 때문이다.

따라서 Python이나 Ruby같은 모던 언어들은 오픈 어드레싱 방식으로 성능을 높이는 대신, 리해싱의 기준 로드 팩터를 작게 잡아 성능 저하 문제를 해결한다.
Python의 경우 기준 로드 팩터는 0.66으로 앞서 살펴본 Java보다 낮으며, Ruby는 0.5로 훨씬 더 작다.

각 언어별 해시 테이블의 구현 방식을 정리하면 다음과 같다.

언어	방식
C++(GCC libstdc++)	개별 체이닝
Java	개별 체이닝
Go	개별 체이닝
Ruby	오픈 어드레싱
Python	오픈 어드레싱