칼만필터 파이썬 코드로 구현하기(Pykalman 패키지 사용)

칼만필터 정의 및 알고리즘

• 앞서 칼만필터 정의 및 알고리즘 내용을 살펴봄. 미리 칼만필터에 대해 알고 이 글을 보는 것을 추천함.
• 그것에 대한 파이썬 패키지인 Pykalman을 사용해 구현함.
• 실제 온도에 대해 칼만필터를 적용함.

1. 데이터 불러오기

# 데이터 지정
true_temperature = np.array(df.col[:600])  # 실제 온도
n_timesteps = len(true_temperature)
measurements = true_temperature + np.random.normal(0, 0.5, n_timesteps)  # 측정된 온도 (노이즈 포함)

• true_temperature는 실제 온도로 지정함.
• measurements는 실제온도에서 노이즈를 추가해줌.
  • 현실 시계에서 측정된 데이터는 항상 일정한 양의 오차나 노이즈를 포함하고 있어 노이즈를 추가해주는 것이 좋음.
  • 센서로 측정한 데이터는 다양한 요인(센서의 정확도, 환경적인 영향 등)으로 인해 실제값과 차이가 날 수 있기 때문에 이러한 오차를 모델링하기 위해 노이즈를 추가함.
  • 모델의 강건성 테스트: 노이즈가 포함된 데이터를 사용함으로써 모델의 강건성을 테스트할 수 있음. 좋은 모델은 노이즈가 있는 데이터에서도 정확한 예측을 할 수 있어야 함.

2. 칼만필터 설정

from pykalman import KalmanFilter
# 칼만 필터 설정
kf = KalmanFilter(
    transition_matrices=[1], # 상태 전이 행렬
    observation_matrices=[1],
    initial_state_mean=true_temperature[0], # 초기값은 실제 데이터의 첫번째 값
    initial_state_covariance=1, # 초기 상태의 공분산
    observation_covariance=1,
    transition_covariance=0.1
)

• transition_matrices : 상태 전이 행렬
  • A(State Transition Matrix)
  • 이전 상태에서 현재 상태로의 전환을 나타냄.
  • [1]인 경우 상태가 선형적으로 변하지 않는다는 것을 의미함. 만약 상태가 시간에 따라 선형적으로 변한다면 다른 값을 사용할 수 있음
• observation_matrices : 관측 행렬
  • H(Measurement Matrix)
  • 실제 상태에서 관측값으로 변환하는 역할.
  • [1]인 경우 상태 값이 직접적으로 관측된다는 것을 의미함.
• observation_covariance : 관측 노이즈의 공분산
  • R(Measurement Noise Covariance)
  • 데이터의 노이즈 수준을 반영하여 적절한 값을 설정함.
  • 측정값의 신뢰도를 나타냄.
  • 일반적으로 1을 시작값으로 사용.
• transition_covariance : 프로세스 노이즈의 공분산
  • Q(Process Noise Covariance)
  • 시스템 모델의 불확실성을 나타내는 값.
  • 시스템의 동작 모델이 불확실할 수록 이 값을 높게 설정함.
  • 일반적으로 0.1로 사용함.

3. 칼만필터 사용

# 칼만 필터를 사용하여 상태 추정
filtered_state_means, filtered_state_covariances = kf.filter(measurements)

• kf.filter() : 칼만필터를 사용하여 관측 데이터로부터 상태 추정함.
• filtered_state_means(covariances) : 각 시점에서 필터링된 상태 추정 값(평균), 공분산행렬

4. 칼만필터 예측 성능 확인

# 예측 성능 비교
def mean_squared_error(true, pred):
    return np.mean((true - pred) ** 2)
    
kf_mse = mean_squared_error(true_temperature, filtered_state_means.reshape(-1,))

print(f'Kalman Filter MSE: {kf_mse:.3f}')
# Kalman Filter MSE: 0.173

• filtered_state_means : 데이터 shape가 (n,1)로 나오는데 true_temperature가 (n,) 라서 reshape를 진행해줌.

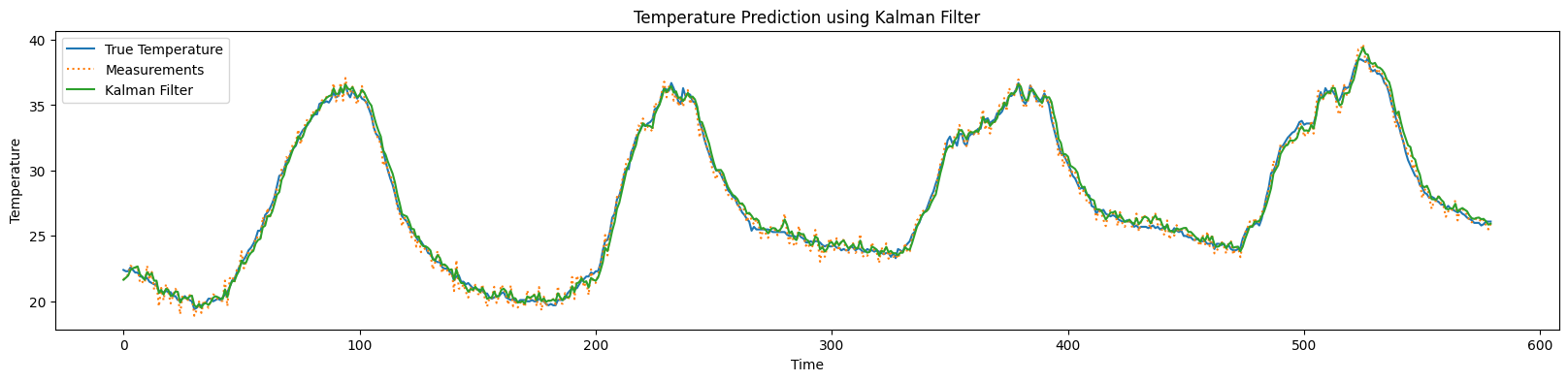
5. 결과 시각화

# 결과 시각화
plt.figure(figsize=(20, 4))
plt.plot(true_temperature, label='True Temperature')
plt.plot(measurements, label='Measurements', linestyle='dotted')
plt.plot(filtered_state_means, label='Kalman Filter')
plt.legend()
plt.xlabel('Time')
plt.ylabel('Temperature')
plt.title('Temperature Prediction using Kalman Filter')
plt.show()