칼만필터 정의

과거와 현재의 관측값을 사용해 미래의 상태를 예측하는 수학적 알고리즘

• 특히, 시스템이 불확실하거나 노이즈가 많은 경우 유용함
• 물체의 특정 시점에서의 상태가 이전 시점의 상태와 선형적인 관계를 가지고 있는 경우 적용이 가능
• 이전 시간 단계의 상태와 공분산을 기반으로 현재 시간 단계의 상태와 공분산을 예측함
• 재귀적 베이지안 필터(recursive Bayesian filter)의 한 유형
  
  
  

칼만필터 알고리즘

• 칼만필터는 예측단계(Prediction Step)와 보정(갱신)단계(Correction Step) 두 단계를 반복함

• 즉, 상태벡터(x)와 오차공분산행렬(P)을 업데이트하여 시스템의 현재 상태를 추정

• 상태: 추적하려는 대상의 현재 상황을 나타냄

• 오차 공분산 행렬(P): 추정된 상태 벡터의 불확실성(분산)을 나타내는 행렬, 즉 상태 변수들 간의 불확실성과 변수들 간의 상관관계를 표현
  
  
  

1. 예측 단계(Prediction Step)

• 이전 시간 단계의 상태와 공분산을 기반으로 현재 시간 단계의 상태와 공분상을 예측함

a. 상태 예측

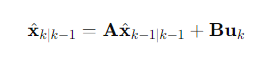
• $x_k|_k-1$ : 시간 k에서의 예측된 상태 벡터(이전 관측치를 반영한 예측)
• $A$ : 상태전이행렬
• $x_k-1|_k-1$ : 시간 k-1에서의 추정된 상태 벡터(이전 단계에서 보정된 상태)
• $B$: 제어입력행렬(제어시스템의 경우에만 사용, 여기서는 B=0로 가정)
• $u_k$: 제어입력(해당되지 않으면 생략)

b. 오차 공분산 예측

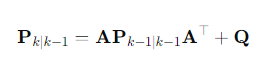
• $P$ : 시간(k,k-1)에서의 예측된 오차 공분산 행렬
• $Q$ : 프로세스 노이즈 공분산 행렬(모델의 불확실성)

2. 보정(갱신) 단계(Correction Step)

• 새로운 관측값을 사용하여 예측된 공분산 보정

a. 칼만이득 단계(Kalman gain)

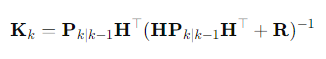
• $K_k$ : 시간 k에서의 칼만 이득 행렬
• $H$ : 관측 행렬
• $R$ : 관측 노이즈 공분산 행렬

b. 상태 보정

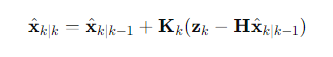
• $x_k|_k$ : 시간 k에서 보정된 상태 벡터
• $z_k$ : 시간k에서의 관측값
• $z_k - Hx_k|_k-1$ : 예측된 관측값과 실제 관측값 사이의 오차(혁신, innovation)

c. 오차 공분산 보정

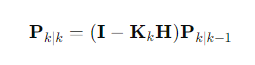
• $P_k|_k$ : 시간 k에서의 보정된 오차 공분산 행렬
• $I$ : 단위 행렬
  
  
  

요약

• 예측 단계는 이전 상태와 시스템 모델을 사용하여 현재 상태와 오차 공분산을 예측, 이는 시스템의 동적 모델을 반영하여 미래 상태를 추정하는 단계
• 보정 단계는 새로운 관측값을 사용하여 예측된 상태를 수정, 이는 실제 관측값을 반영하여 예측의 정확성을 높이는 단계

  칼만필터는 이 두 단계를 반복하여, 시간에 따라 시스템의 상태를 점진적으로 정확하게 추정함.