백 트래킹

백 트래킹

백 트래킹 또는 퇴각 검색이라고 부른다.

제약 조건 만족 문제에서 해를 찾기 위한 전략이다.

• 해를 찾기 위해 후보군에 제약 조건을 저진적으로 체크하다가, 해당 후보군이 제약 조건을 만족할 수 없다고 판단되는 즉시 backtrack(다시는 이 후보군을 체크하지 않을 것을 표기)하고, 바로 다른 후보군으로 넘어가며, 결국 최적의 해를 찾는 방법이다.

실제 구현시 고려할 수 있는 모든 경우의 수(후보군)를 상태공간트리를 통해 표현한다.

• 각 후보군을 DFS 방식으로 확인한다.
• 상태 공간 트리를 탐색하면서 제약이 맞지 않으면 해의 후보가 될만한 곳으로 바로 넘어가서 탐색한다.
  • Promising : 해당 루트가 조건에 맞는지를 검사하는 기법
  • Pruning(가지치기) : 조건에 맞지 않으면 포기하고 다른 루트로 바로 돌아서서 탐색의 시간을 절약하는 기법

즉 백트래킹은 트리 구조를 기반으로 DFS로 깊이 탐색을 진행하면서 각 루트에 대해 조건에 부합하는지 체크(Promising), 만약 해당 트리에서 조건이 맞지 않는 노드는 더 이상 DFS로 깊이 탐색을 진행하지 않고 가지를 쳐버린다.(Pruning)

상태 공간 트리

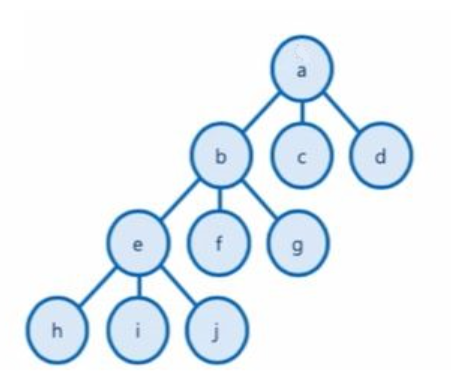
문제 해결 과정의 중간 상태를 각각의 노드로 나타낸 트리

예제 문제

N Queen 문제

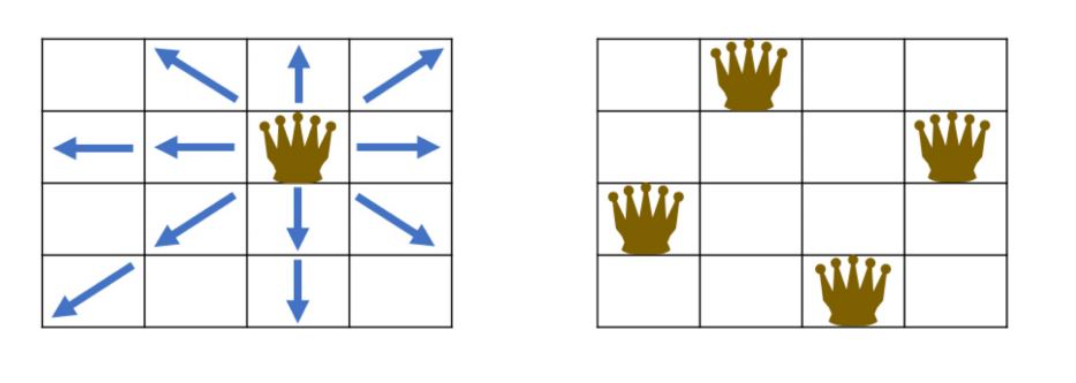
N x N 크기의 체스판에 N개의퀸을 서로 공격할 수 없도록 배치하는 문제
퀸은 다음과 같이 이동할 수 있으므로 배치된 퀸 간에공격할 수 없는 위치로 배치해야 한다.

Pruning(가지치기) for N Queen 문제

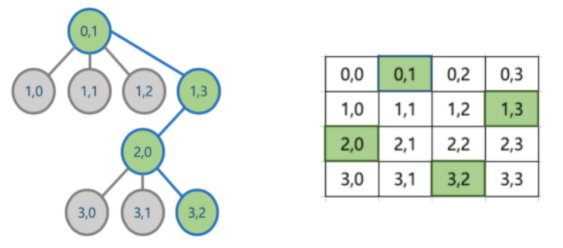
• 한 행에는 하나의 퀸 밖에 위치할 수 밖에 없다. (퀸은 수평 이동이 가능하기 떄문)
• 맨 위에 있는행부터 퀸을 배치하고 다음 행에 해당 퀸이 이동할 수 없는 위치를 찾아 퀸을 배치한다.
• 만약 앞선 행에 배치한 퀸으로 인해, 다음 행에 해당 퀸들이 이동할 수 없는 위치가 없을 경우에는 더 이상 퀸을 배치하지 않고 이전 행의 퀸의 배치를 바꾼다.
• 즉 맨 위의 행부터 전체 행까지 퀸의 배치가 가능한 경우의 수를 상태 공간 트리 형태로 만든 후 각 경우를 맨 위의 행부터 DFS 방식으로 접근, 해당 경우가 진행이 어려울 경우, 더 이상 진행하지 않고 다른 경우를 체크하는 방식이다.

Promising for N Queen 문제

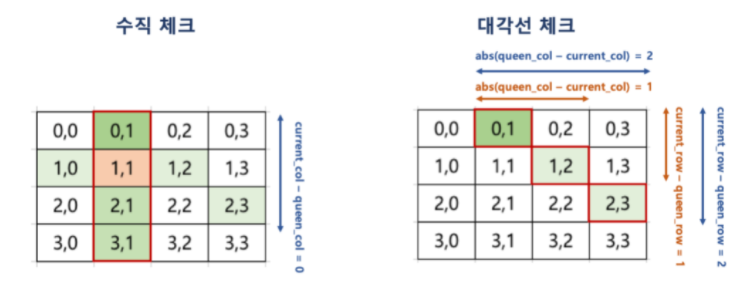
• 해당 루트가 조건에 맞는지를 검사하는 기법을 활용한다.
• 현재까지 앞선 행에서 배치한 퀸이 이동할 수 없는 위치가 있는지를 다음과 같은 조건으로 확인한다.
  • 한 행에 어차피 하나의 퀸만 배치 가능하므로 수평체크는 별도로 필요하지 않다.

예제 코드

    public void dfs(int n, int currentRow, Stack<Integer> currentCandidate) {

        if (currentRow == n) {
            System.out.println(currentCandidate);
            return;
        }

        for (int i = 0; i < n; i++) {
            if (isAvailable(currentCandidate, i)) {
                currentCandidate.add(i);
                dfs(n, currentRow + 1, currentCandidate);
                currentCandidate.pop();
            }

        }
    }

    private boolean isAvailable(Stack<Integer> candidate, int currentCol) {
        final int currentRow = candidate.size();
        for (int i = 0; i < currentRow; i++) {
            if ((candidate.get(i) == currentCol) || (Math.abs(candidate.get(i) - currentCol) == currentRow - i)) {
                return false;
            }
        }
        return true;
    }

    public static void main(String[] args) {
        final NQueen T = new NQueen();
        T.dfs(4, 0, new Stack<Integer>());
    }