최단 경로 문제란?
두 노드를 잇는 가장 짧은 경로를 찾는 문제다.
가중치 그래프 (Weighted Graph)에서 간선(Edge)의 가중치 합이 최소가 되도록 하는 경로를 찾는 것이 목적이다.
최단 경로 문제의 종류
1. 단일 출발 최단 경로 문제
- 그래프 내의 특정 노드 u에서 출발하여 그래프 내의 모든 다른 노드에 도착하는 짧은 경로를 찾는 문제
2. 단일 도착 최단 경로 문제
- 모든 노드들로부터 출발해서 그래프 내의 특정 노드 u에 도착하는 가장 짧은 경로를 찾는 문제
3. 단일 쌍 최단 경로 문제
- 주어진 노드 u 와 v 간의 최단 경로를 찾는 문제
4. 전체 쌍 최단 경로 : 그래프 내의 모든 노드 쌍(u,v) 사이에 대한 최단 경로를 찾는 문제
다익스트라 알고리즘
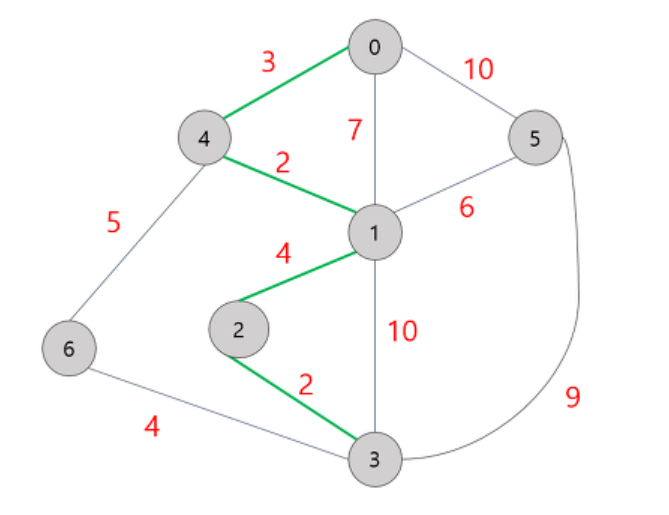
하나의 정점에서 다른 모든 정점에 도착하는 가장 짧은 거리를 구하는 문제(1. 단일 출발 최단 경로 문제)다.
다익스트라 알고리즘 로직
- 첫 정점을 기준으로 연결되어 있는 정점들을 추가해 가며, 최단 거리는 갱신하는 기법
- 다익스트라 알고리즘은 BFS와 유사하다.
- 첫 정점부터 각 노드간의 거리를 저장하는 배열을 만든 후, 첫 정점의 인접 노드 간의 거리부터 먼저 계산하면서, 첫 정점부터 해당 노드간의 가장 짧은 거리를 해당 배열에 업데이트 한다.
우선 순위 큐를 활용한 다익스트라 알고리즘
우선순위 큐는 MinHeap 방식을 활용해서 현재 가장 짧은 거리를 가진 노드 정보를 먼저 꺼내게 된다.
- 첫 정점을 기준으로 배열을 선언하여 첫 정점에서 각 정점까지의 거리를 저장한다.
- 초기에는 첫 정점의 거리는 0, 나머지는 무한대로 저장한다.(inf라고 표현한다.)
- 우선순위 큐에 (첫 정점, 거리 0)만 먼저 넣는다.
- 우선순위 큐에서 노드를 꺼낸다.
- 처음에는 첫 정점만 저장되어 있으므로, 첫 정점이 꺼내진다.
- 첫 정점에 인접한 노드들 각각에 대해, 첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 정점에서 각 정점까지의 거리를 비교한다.
- 배열에 저장되어 있는 거리보다, 첫 정점에서 해당 노드로 가는 거리가 더 짧을 경우, 배열에 해당 노드의 거리를 업데이트한다.
- 배열에 해당노드의 거리가 업데이트된 경우, 우선순위 큐에 넣는다.
- 결과적으로 BFS 방식과 유사하게, 첫 정점에 인접한 노드들을 순차적으로 방문하게 된다.
- 만약 배열에 기록된 현재까지의 발견된 가장 짧은 거리보다, 더 긴 거리(루트)를 가진 (노드,거리)의 경우에는 해당 노드와 인접한 노드간의 거리 계산을 하지 않는다.
- 2번의 과정을 우선순위 큐에 꺼낼 노드가 없을 때까지 반복한다.
예제
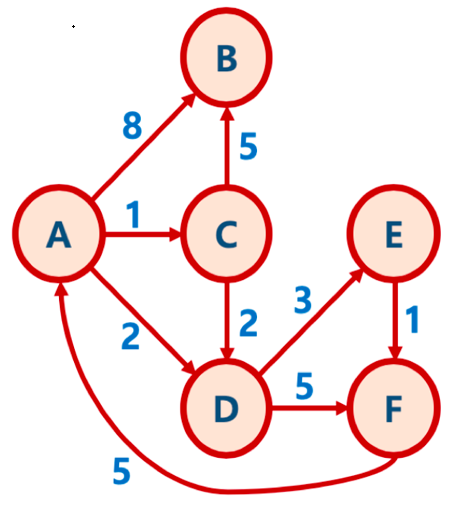
거리 저장 배열
우선순위 큐
큐에서 추출 : A, 0
거리 저장 배열
우선순위 큐
큐에서 추출 : A, 0
거리 저장 배열
우선순위 큐
큐에서 추출 : A, 0
거리 저장 배열
우선순위 큐
큐에서 추출 : C, 1
거리 저장 배열
우선순위 큐
큐에서 추출 : D, 2
거리 저장 배열
우선순위 큐
큐에서 추출 : D, 2
거리 저장 배열
우선순위 큐
큐에서 추출 : E, 5
거리 저장 배열
우선순위 큐
큐에서 추출 : B, 6
거리 저장 배열
우선순위 큐
큐에서 추출 : F, 6
거리 저장 배열
우선순위 큐
큐에서 추출 : F, 7
거리 저장 배열
우선순위 큐
큐에서 추출 : B, 8
거리 저장 배열
우선순위 큐
예제 코드
Edge edgeNode;
int currentDistance, weight, distance;
String currentNode, adjacent;
List<Edge> nodeList;
public HashMap<String,Integer> solution(HashMap<String, List<Edge>> graph, String start) {
HashMap<String, Integer> distances = new HashMap<>();
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>();
for (String key : graph.keySet()) {
distances.put(key, Integer.MAX_VALUE);
}
distances.put(start, 0);
priorityQueue.add(Edge.of(0, start));
while (!priorityQueue.isEmpty()) {
edgeNode = priorityQueue.poll();
currentDistance = edgeNode.getDistance();
currentNode = edgeNode.getVertex();
if (distances.get(currentNode) < currentDistance) {
continue;
}
nodeList = graph.get(currentNode);
for (Edge adjacentNode : nodeList) {
adjacent = adjacentNode.getVertex();
weight = adjacentNode.getDistance();
distance = currentDistance + weight;
if (distance < distances.get(adjacent)) {
distances.put(adjacent, distance);
priorityQueue.add(Edge.of(distance, adjacent));
}
}
}
return distances;
}
public static void main(String[] args) {
final DijkstraExam T = new DijkstraExam();
HashMap<String, List<Edge>> graph = new HashMap<>();
graph.put("A", new ArrayList<>(
Arrays.asList(
Edge.of(8,"B"),
Edge.of(1,"C"),
Edge.of(2,"D")
)));
graph.put("B", new ArrayList<>());
graph.put("C", new ArrayList<>(
Arrays.asList(
Edge.of(5,"B"),
Edge.of(2,"D")
)));
graph.put("D", new ArrayList<>(
Arrays.asList(
Edge.of(3,"E"),
Edge.of(5,"F")
)));
graph.put("E", new ArrayList<>(
Arrays.asList(
Edge.of(1,"F")
)));
graph.put("F", new ArrayList<>(
Arrays.asList(
Edge.of(5,"A")
)));
System.out.println(T.solution(graph, "A"));
}
우선 순위 큐 사용 장점
지금까지 발견된 가장 짧은 거리의 노드에 대해서 먼저 계산한다.
따라서 더 긴 거리로 계산된 루트에 대해서는 계산을 스킵할 수 있다.
PriorityQueue
PriorityQueue는 내부적으로 정렬 기능을 수행한다.
따라서 PriorityQueue에 넣어지는 특별한 형태의 객체의 경우 객체간의 정렬을 위한 기준을 정의해야 한다.
PriorityQueue에서 내부적으로 정렬 기능을 사용할때는 해당 객체의 Comparable 인터페이스의 compareTo() 메소드를 호출하므로 객체간 정렬 기준을 정의하기 위해 Comparable 인터페이스의 compareTo() 메소드를 정의해줘야 한다.
시간 복잡도
다익스트라 알고리즘은 크게 두 가지 과정을 거친다.
1. 각 노드마다 인접한 간선들을 모두 검사하는 과정
2. 우선순위 큐에 노드.거리 정보를 넣고 삭제하는 과정
각 과정별 시간 복잡도
1. 각 노드는 최대 한번씩 방문하므로, 그래프의 모든 간선은 최대 한 번 씩 검사한다.
- 각 노드마다 인접한 간선들을 모두 검사하는 과정은 O(E) 시간이 걸린다.
- 우선순위 큐에 가장 많은 노드, 거리 정보가 들어가는 경우, 우선 순위 큐에 노드/거리 정보를 넣고 삭제하는 과정에서 최악의 시간이 걸린다.
- 우선순위 큐에 가장 많은 노드 거리 정보가 들어가는 시나리오는 그래프의 모든 간선이 검사될 때마다, 배열의 최단 거리가 갱신되고, 우선 순위 큐에 노드/거리가 추가되는 것이다.
- 이 때 추가는 각 간선마다 최대 한 번 일어날 수 있으므로, 최대 O(E) 시간이 걸리고 O(E)개의 노드/거리 정보에 대해 우선순위 큐를 유지하는 작업은 O(logE)가 걸린다.
- 따라서 해당 과정의 시간 복잡도는 O(ElogE)
총 시간 복잡도
O(E) + O(ElogE) = O(ElogE)


