고정소수점

움직이지 않고 고정된 소수점을 뜻한다.

32비트 체계라고 가정한다면

부호 비트
(0은 양수, 1은 음수)

정수부
정수부분이 저장된다

소수부
소수부분이 저장된다

예를 들어보자
5.75를 2진수로 변환하면
5.75 = 101.11(2)
양수 이므로 부호비트에는 0이 저장되고
101은 정수부에, 11은 소수부에 저장 된다.
0|000000000000101|1100000000000000

IEEE754 부동소수점

고정되지 않고 움직이는 소수점을 뜻한다.

32비트 체계라고 가정한다면

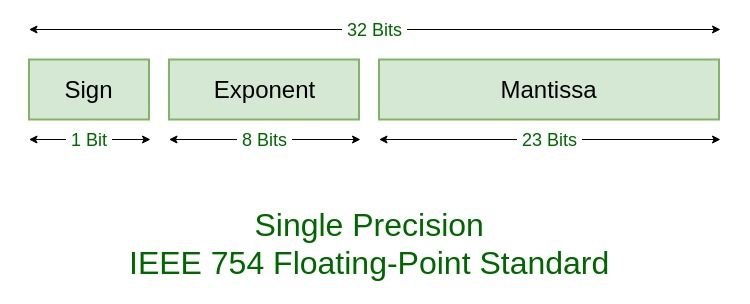
Sign(부호 비트)는 1bit를 가지며 부호를 나타낸다.
(0은 양수, 1은 음수)

Exponent(지수부)는 8bits를 가진다.
Bias(127)를 적용하여 저장
실제 지수 값 = 저장된 값 - 127
예를 들어, 저장된 지수 값이 130이라면 실제 지수는 130 - 127 = 3

Mantissa(가수부)는 23bit를 가진다.
정규화된 수는 1.XXXXX… × 2^E 형태를 따름
따라서, 1. 부분은 암묵적으로 존재
저장된 값은 XXXXX… 부분만 저장됨

예를 들어보자
5.75를 IEEE 754 32비트로 변환해보자

5.75 = 101.11(2)
이런식으로 이진수로 변화 시킨 후

이 101.11(2) 정규화를 시키면

1.0111 × 2^2 이런 식으로 나타낼 수 있다.
(만약 소수점이 뒤로 간다면 뒤로 간 만큼 새고 지수에 -를 붙인다.)
예 0.0010001 - > 1.0001 × 2^-3

그럼 일단 양수이므로 최상위 비트(부호 비트)는 0이 되며

지수의 값이 1.0111 × 2^ 2
2 이므로 127 + 2를 하여 129를 지수부에 표시하면 된다.

그리고 남은 0111을 가수부에 표시하면 된다

완성 후
0 | 10000001 | 01110000000000000000000