들어가기 전에

이전에 탐색이라고 하면 리스트의 탐색만을 다뤘다. 탐색 기법으로는 이진 탐색, 순차 탐색을 학습하였는데 이번에는 그래프의 탐색을 배워볼 것이다.

그래프의 탐색

그래프의 대표 적인 탐색
1. 너비 우선 탐색(BFS)
2. 깊이 우선 탐색(DFS)

그래프의 표기 방법

그래프의 표기는 딕셔너리와 리스트 자료구조를 통해서 표현한다.
해당 노드와 간선으로 연결된 노드들을 입력해준다.

graph = dict()
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']

너비 우선 탐색 (BFS)

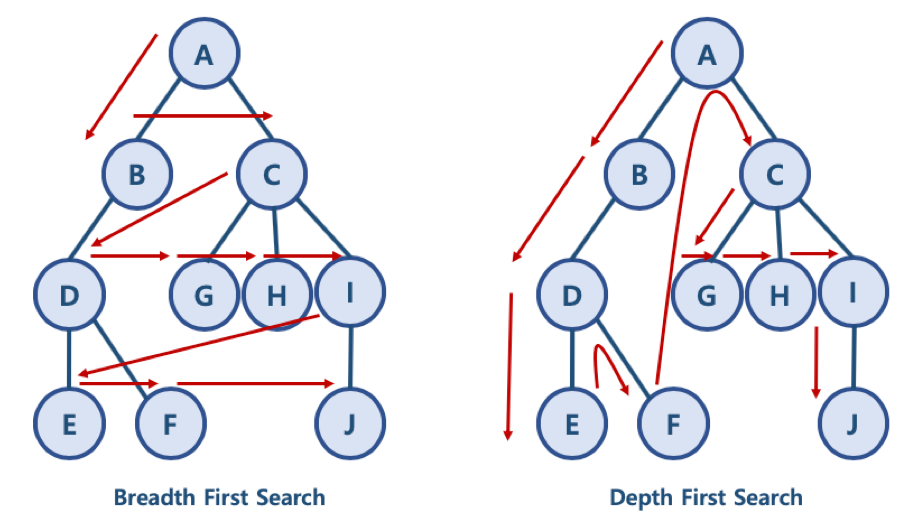
같은 레벨에 있는 노드들을 먼저 탐색하는 기법

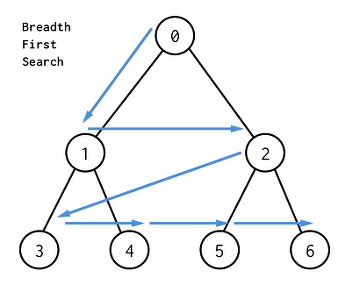
시작 노드에서 파생된 노드들을 먼저 탐색을 하고 그렇게 파생된 노드들에서 또 새롭게 파생된 노드 순으로 탐색을 하는 것이 BFS 탐색이다.

BFS 코드로 표현

너비 우선 탐색(BFS)는 1개의 딕셔너리와 2개의 큐(리스트)가 필요한다.

1. need_visit에서 값 가져오기
2. visited에 있는 값인지 확인 (처음 방문했는지 확인)
3. 처음 방문한 것이라면 visited에 값 추가 후 빠진 값에 해당하는 값 need에 추가
4. 처음 방문한 것이 아니라면 visited에 추가하지 않고 넘어간다

def BFS(graph, start_node):
    visited , need_visit = list(),list() # 두개의 큐(리스트) 선언
    need_visit.append(start_node) # 시작점을 리스트에 삽입
    
    while need_visit: # 방문이 필요한 노드가 있을 동안 반복
        node = need_visit.pop(0) # need 리스트의 맨 앞요소 pop
        
        if node not in visited: # need 리스트에서 pop한 값이 visited 리스트에 있지 않는 경우
                                # 이미 방문한 것인지 확인하는 용도
            visited.append(node) # 방문을 하지 않았다면 visited에 추가
            need_visit.extend(graph[node]) # need에 새롭게 추가된 값 입력
    
    return visited

깊이 우선 탐색 (DFS)

한 노드의 자식을 끝까지 타고 순회한 뒤에 다른 형제들의 자식을 타고 다시 끝까지 내려가며 순회하는 방법을 DFS라고 한다.

DFS 코드로 표현

깊이 우선 탐색(DFS) 는 1개의 딕셔너리와 2개의 리스트가 필요한데 1개는 큐로 다른 1개는 스택으로 사용한다.

def DFS(graph, start_node):
	need_visit, visited = list(),list()
    need_visit.append(start_node)
    
    while need_visit:
    	node = need_visit.pop()
        if node not in visited:
        	visited.append(node)
            need_visit.extend(graphp[node])
    
    return visited

DFS와 BFS는 차이

DFS와 BFS의 차이는 큐로 2개를 사용하는지 큐 1개 스택 1개를 사용하는지 차이가 있다.