알고리즘

알고리즘(정렬)

탐색

트리

자료구조와 알고리즘

이진 트리와 이진 탐색 트리

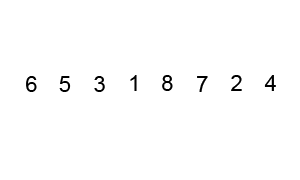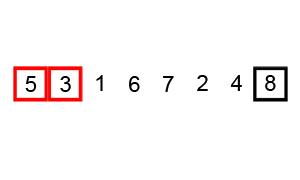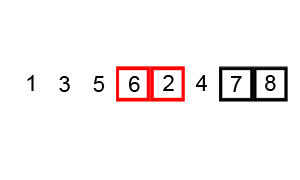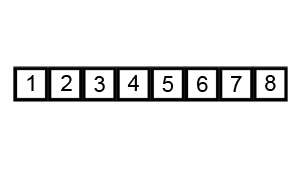
즉 a1,a2,a3,a4가 있다고 하면 a1,a2를 비교하고 더 큰 수를 a3과 비교하고 그 중 더 큰 수를 a4와 비교하면 된다. 만약에 a1,a2,a3,a4가 각각 1,4,3,2이라고 가정하고 진행해보자a1,a2(1,4)를 비교하면 a2가 더 크다 그러므로 a3과

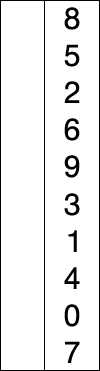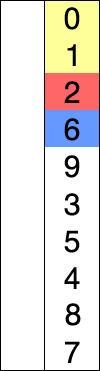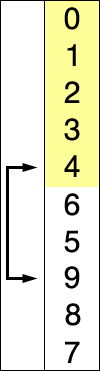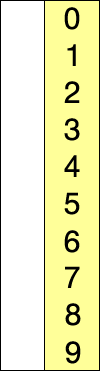
선택 정렬은 기본 정렬중에서 가장 쉽게 생각 할 수 있는 정렬 방식이다.선택 정렬의 컨셉은 전체의 값을 비교해보고 가장 작은 수를 가장 앞으로 보내는 방식을 취하고 있다.따라서 a1,a2,a3,a4가 각각 1,4,3,2 라고하면 우선 a1,a2,a3,a4를 전체다 비교

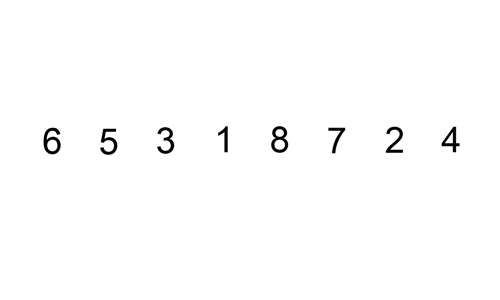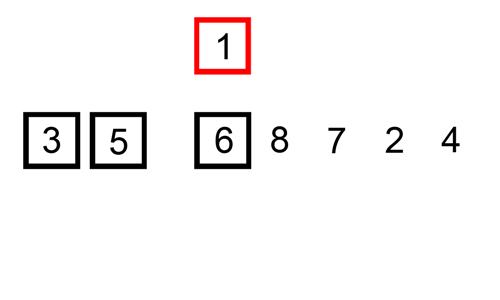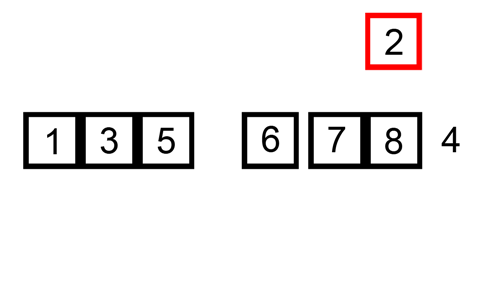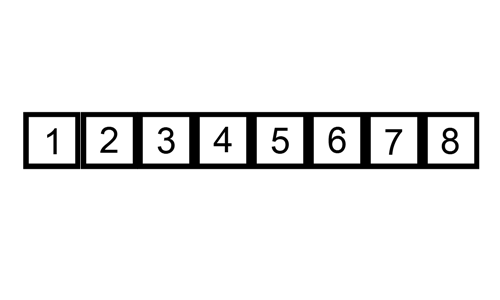
삽입 정렬은 하나의 값을 기준으로 잡고 그 기준 값이 앞의 값보다 클 때 까지 교환해주는 것이 삽입 정렬이다.예를들어 5,3,4,2,1이 있다고 하면1번째 턴에서는 3,5,4,2,12번째 턴에서는 3,4,5,2,13번째 턴에서는 3,4,2,5,1 => 3,2,4,5,1

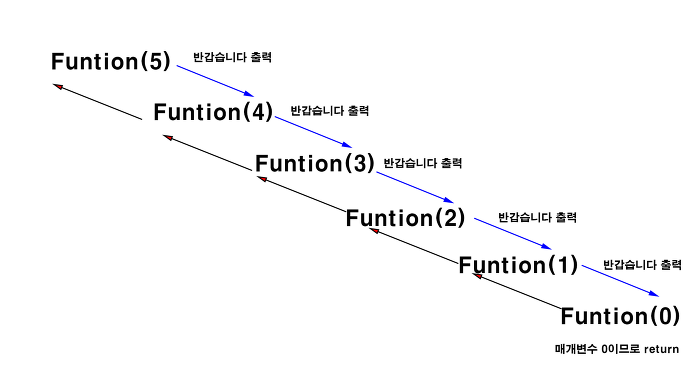
재귀 용법 재귀 용법 (recursive call) 재귀 용법은 쉽게 말해서 팩토리얼이라고 생각하면 된다. 함수의 반환값이 함수인 경우 5! = 5 x 4 x 3 x 2 x 1 6! = 6 x 5 x 3 x 2 x 1 = 6 x 5! = 6 x 5 x 4! n! =

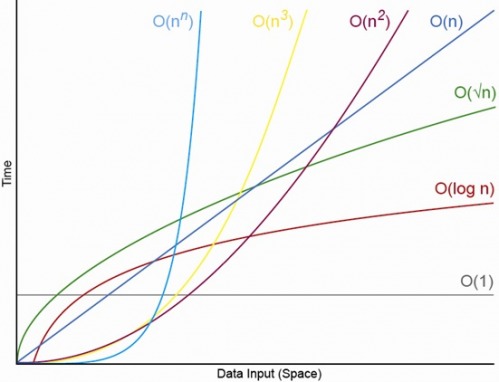
자료구조는 더 효과적으로 자료를 저장하기 위한 방법이고 알고리즘은 이렇게 저정된 메모리를 더 효과적으로 사용할 수 있게하기 위한 방법이다. 그렇다면 어떻게 이 방법이 효과적인지 아닌지를 판별할수 있는 기준이 있어야 한다. 시간 복잡도는 반복문에 의해서 결정된다. 그 이

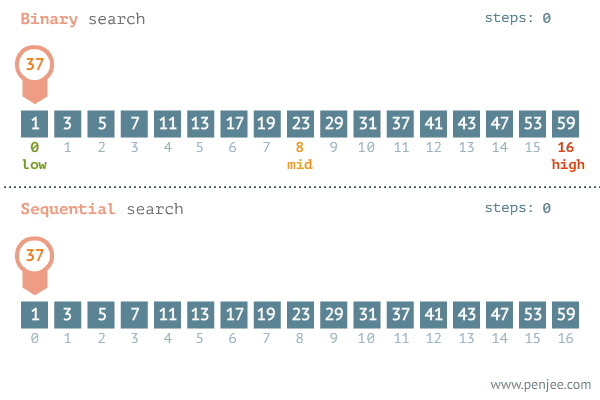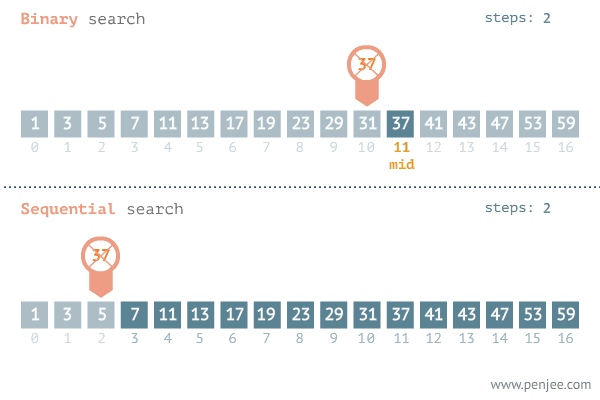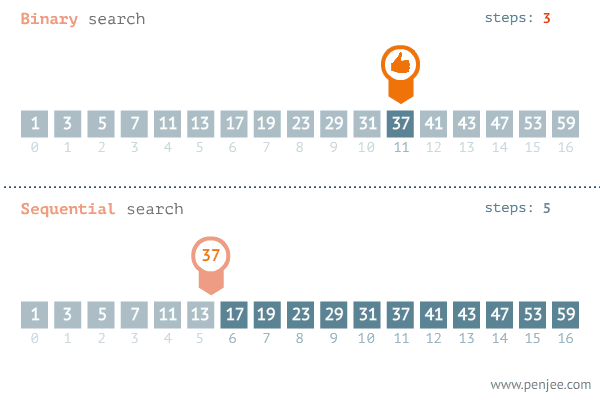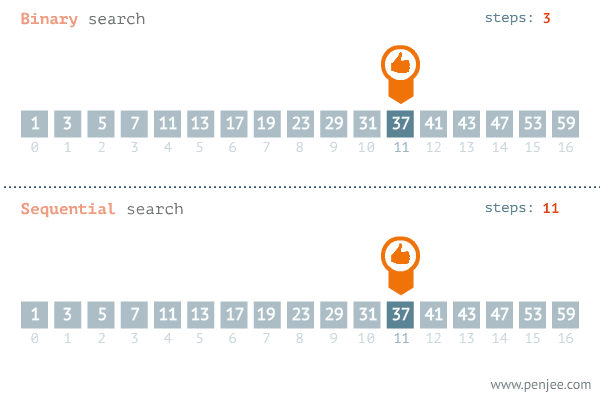
정렬은 특정 데이터안에서 내가 원하는 (조건에 맞는) 데이터가 존재하는지를 확인하는 작업을 의미한다.탐색도 정렬과 마찬가지로 고급 탐색이 있고 기본 탐색이 있다. 일반적으로 가장 쉽게 떠올릴 수 있는 탐색의 방법은 무식하게 처음부터 끝까지 내가 원하는 조건의 데이터가

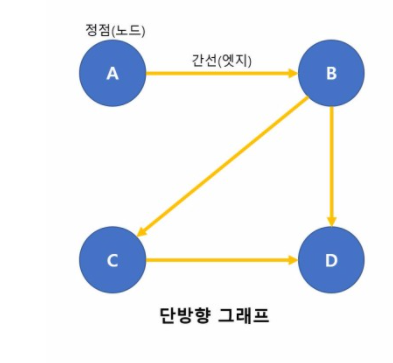
그래프는 정점 혹은 노드 or 간선으로 표현한 것을 그래프라고 한다. 내가 생각 했을 때 그래프는 길 찾기 문제를 풀 때 혹은 최단거리 같은 문제를 풀때 그래프라는 말을 들어본 것 같다.노드: 위치를 말함, 정점이라고도 함간선: 위치 간의 관계를 표시한 선 , 노드를

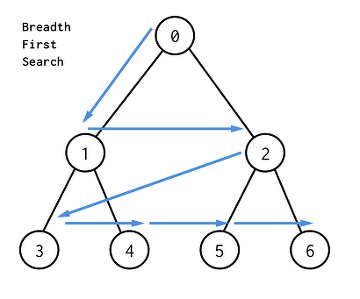
들어가기 전에 이전에 탐색이라고 하면 리스트의 탐색만을 다뤘다. 탐색 기법으로는 이진 탐색, 순차 탐색을 학습하였는데 이번에는 그래프의 탐색을 배워볼 것이다. 그래프의 탐색 그래프의 대표 적인 탐색 너비 우선 탐색(BFS) 깊이 우선 탐색(DFS) 그래프의

탐욕 알고리즘(greedy algorithm)은 코테에서 가장 많이 등장하는 알고리즘 유형이다. 반드시 알고 넘어가야하는 중요한 알고리즘이다. 탐욕 알고리즘의 특징은 여러개의 선택지가 주어지고 그 중 하나를 선택해야 할 때 매 순간 최적의 방법을 선택하는 방식으로 진행