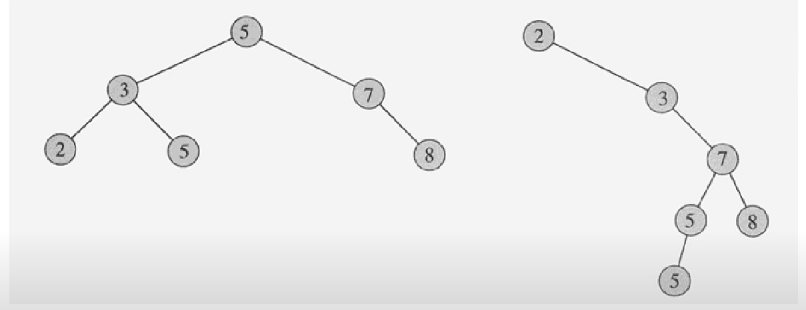
BST

1. 여러개의 키(key)를 저장
2. insert, search, delete 연산을 지원하는 자료구조
3. node와 branch를 이용하여, 사이클이 이루어지지않도록 구성한 자료구조.

트리의 구조

• 트리: node와 branch를 이용해서 사이클을 이루지않도록 구성한 데이터구조
• BST는, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨

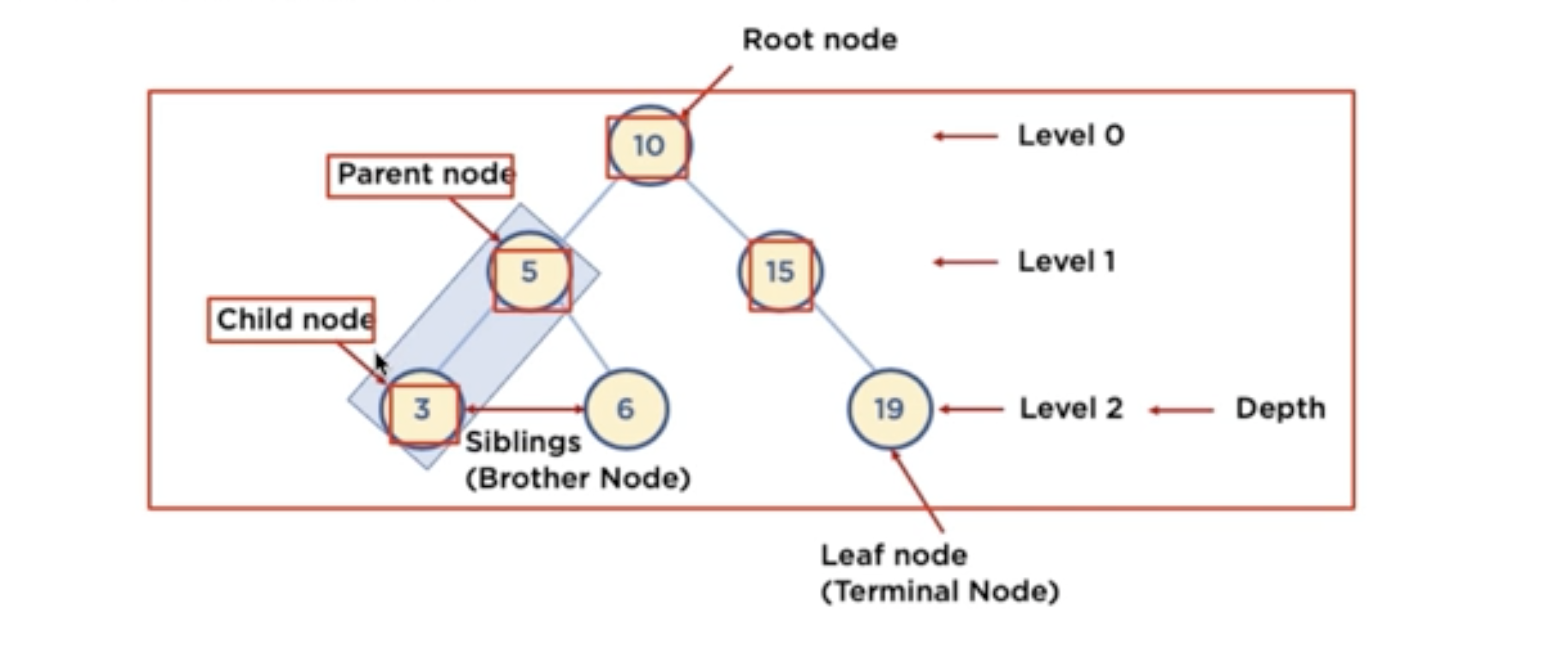
용어

• node: 트리에서 데이터를 저장하는 기본요소
• Root node: 최상단의 위치한 노드
• level : 최상위노드를 level 0으로 하였을때, 하위 branch로 연결된 노드이 깊이를 나타낸다.
• Parent, child노드 : 어떤노드의 상위, 하위노드
• leaf node (terminal node): child(하위)노드가 하나도 없는 노드
• sibling : 동일한 상위 부모노드를 가진 노드
• Depth: 트리에서 노드가 가질수있는 최대의 level

---

Search

시간복잡도: O(h)
h는 트리의 높이를 뜻함

// version 1
Tree-Search(x, k)	// x == 트리노드, k == 찾는값
{
	// CASE1 : x가 널값이거나, x의 값이 k일때
	if (x == NULL || k = key[x])
    	return x;
    // CASE2 : CASE1이 아닐경우, 왼쪽이나, 오른쪽의 서브트리로 내려감
    if (k < key[x])
    	return Tree-Search(left[x], k);
    else
    	return Tree-Search(right[x], k);
}

// version 2
Tree-Search(x, k)
{
	while (x != NULL && k != key[x])
    {
    	if (x < key[x])
        	x = left[x];
        else
        	x = right[x];
     }
     return x;
}

---

Minimun

최소값은 항상 가장 왼쪽 노드 끝에 존재
시간복잡도: O(h)

Tree-Minimun(x)
{
	while (left[x])
    	x = left[x];
    return x;
}

---

Successor

나보다 크면서 가장작은값: 바로 위의 값

CASE1 : 오른쪽 부트리가 존재할 경우, 오른쪽 부트리에서의 최소값
CASE2 : 오른쪽 부트리가 존재하지 않을경우, 부모를 따라 루트까지 올라가면서, 처음으로
누군가의 왼쪽자식이 되는경우.
CASE3 : CASE2에서 그런 노드가존재하지않는다면, 본인노드가 최대값이다. successor는 없다.

Tree-Succesor(x)
{
	// CASE1
	if (right[x])
    	return Tree-Minimum(x);
        
    // CASE2, CASE3
    y = parent[x];
    while (y && x = right[y])	//	x가 부모의 오른쪽자식인동안
    {
    	x = y;
        y = parent[y];
   	}
    return y;	
}

---

Predecessor

본인노드보다 가장 작으면서 큰 키를 가진 노드 (successor와 반대)
successor와 같다. right를 left로 바꿔주면끝.

Tree-Predecessor(x)
{
	// CASE1
	if (left[x])
    	return Tree-Minimum(x);
        
    // CASE2, CASE3
    y = parent[x];
    while (y && x = left[y])	//	x가 부모의 오른쪽자식인동안
    {
    	x = y;
        y = parent[y];
   	}
    return y;	
}

---

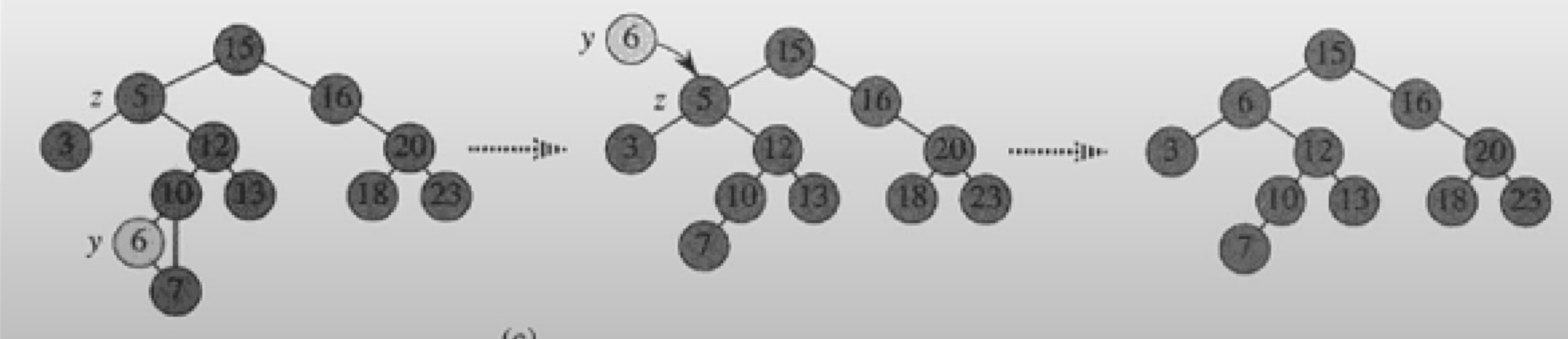
Insert

기존의 노드를 변경하지않고, 추가만한다.

Tree-Insert(T, z)
{
	y = NULL;	//	루트부터 시작하는 x를 따라오는 노드.
    			// z의 자리를 찾기위해서, search를 하는동안,
                // x는 NULL이 되므로, y가 필요.
    x = root[T];
    
    while (x)
    {
    	y = x;
        if (key[z] < key[x])
        	x = left[x];
        else
        	x = right[x];
    }
    
    parent[z] = x;
    if (y == NULL)
    	root[T] = z;
    else if (key[z] < key[y])
    	left[y] = z;
    else
    	right[y] = z;
}

---

Delete

시간복잡도: O(h)
Search를 하여, 삭제할 노드를찾은후에 삭제.
즉, Search를 포함한다.

CASE1 : 자식노드가 없는경우

부모노드의 자식노드를 NULL값으로 바꾸면 끝

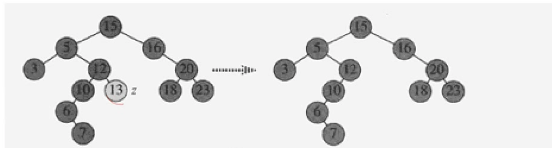
CASE2 : 자식노드가 1개인 경우

나의 자식노드를 부모노드와 연결해주면된다.

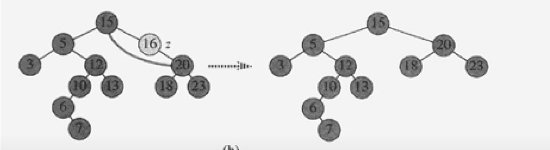
CASE3 : 자식노드가 2개인 경우

삭제하려는 노드의 데이터를 노드의 successor의 데이터를 카피한다.
(자식이 2개인경우이므로, 무조건 successor가 존재한다.)
그후에, successor를 CASE1 또는 CASE2를 이용하여 노드를 정리한다.
(successor노드는 왼쪽노드가없으므로, CASE1이나 CASE2의 경우중 하나이다.)

Tree-Delete(T, z)
{
	// y : 실제로 삭제할 노드
    if (left[z] == NULL || right[z] == NULL) // CASE1, CASE2
    	y = z;
    else	// CASE3
    	y = Tress-Successor(z);
    
    // left가 NULL이 아니라는말은, CASE2에 해당.
    // successor는 왼쪽자식이없다.
    // 노드 y를 삭제, 자식이 0개거나 1개일경우
    // x : 삭제할 노드의 자식노드
	if (left[y] != NULL)	
    	x = left[y];
    else
    	x = right[y];
    // y(삭제할 노드)의 자식노드의 부모가된다.
    if (x != NULL)
    	parent[x] = parent[y];
    
    // 삭제할 노드의 부모노드가 존재하지않는다면, 그 노드는 루트노드.
    if (parent[y] == NULL)
		root[T] = x;
    else if (y == left[ parent[y] ])	//	부모노드와 자식노드를 연결
    	left[ parent[y] ] = x;
    else
    	right[ parent[y] ] = x;
    
    // CASE3
    if (y != x)
    	key[z] = key[y];
    
    return y;
}