RB tree
이진탐색트리의 일종.
균형 잡힌 트리 : 높이가 O(logn)
Search, Insert, Delete 연산을 최악의 경우에도 O(logn) 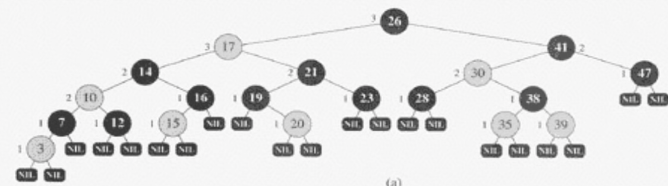
RB tree의 특징
- 각 노드는 하나의 키, 왼쪽자식, 오른쪽자식 그리고 부모노드의 주소를 저장.
- 자식노드가 존재하지 않을 경우 NIL 노드라고 부르는 특수한 노드가 있다고가정.
- 따라서 모든 리프노드는 NIL노드.
- 루트의 보모도 NIL노드라고 가정.
- 노드들은 내부노드와 NIL노드로 분류.
RB tree의 규칙
- 각 노드는 red 혹인 black이다.
- 루트노드는 black이다.
- 모든 리프노드(즉, NIL노드)는 black이다.
- red노드의 자식노드들은 전부 black이다. (즉, red노드들은 연속되지않는다.)
- 모든 노드에 대해서 그 노드로부터 자손인 리프노드에 이르는 모든 경로에는 동일한 개수의 black노드가 존재한다.
Left and Right Rotation
시간복잡도 : O(1)
이진탐색트리의 특성을 유지
a < x < b < y < r
Left Rotation
시간복잡도: O(1)- y = right[x] != NIL 이라고 가정.
- 루트노드의 부모도 NIL이라고 가정.
Left-Rotate(T, x) // x를 기준으로, y와 left rotate
{
y = right[x];
// x와 b를 연결한다.
// 1. y의 왼쪽자식 (b)를 x의 오른쪽 자식으로 만든다.
right[x] = left[y];
// 2. b를 x의 오른쯕 자식으로 만든다.
parent[ left[y] ] = x;
// x의 부모노드를 y의 부모노드로 만든다.
parent[y] = parent[x];
// x의 부모를 y와 연결
// x가 root일 경우, y가 root가 된다.
if (parent[x] == NIL[T])
root[T] = y;
else if (x == left[ parent[x] ])
left[ parent[x] ] = y;
else
right[ parent[x] ] = y;
// x와 y의 연결
left[y] = x;
parent[x] = y;
}Insert
- 보통의 BST에서처럼 노드를 Insert한다.
- 새로운 노드 z를 red노드로 한다.
- RB-Insert-Fixup을 호출한다.
RB-Insert(T, z)
{
x = NIL[T];
y = Root[T];
while (x)
{
y = x;
if (key[z] < key[x])
x = left[x];
else
x = right[x];
}
parent[z] = y;
if (y == NIL[T])
Root[T] = z;
else if (key[z] < key[y])
left[y] = z;
else
right[y] = z;
left[z] = NIL[T];
right[z] = NIL[Y];
color[z] = RED;
RB-Insert-Fixup(T, z);
}
RB_Insert_Fixup
위의 insert함수에서 RB-Insert-Fixup이 나오기전까지
이진탐색트리의 insert와 같다.
하지만 그대로 끝낸다면, 위반될수있는 조건들이 있다.
시간복잡도: O(logn)위반될수있는 조건들
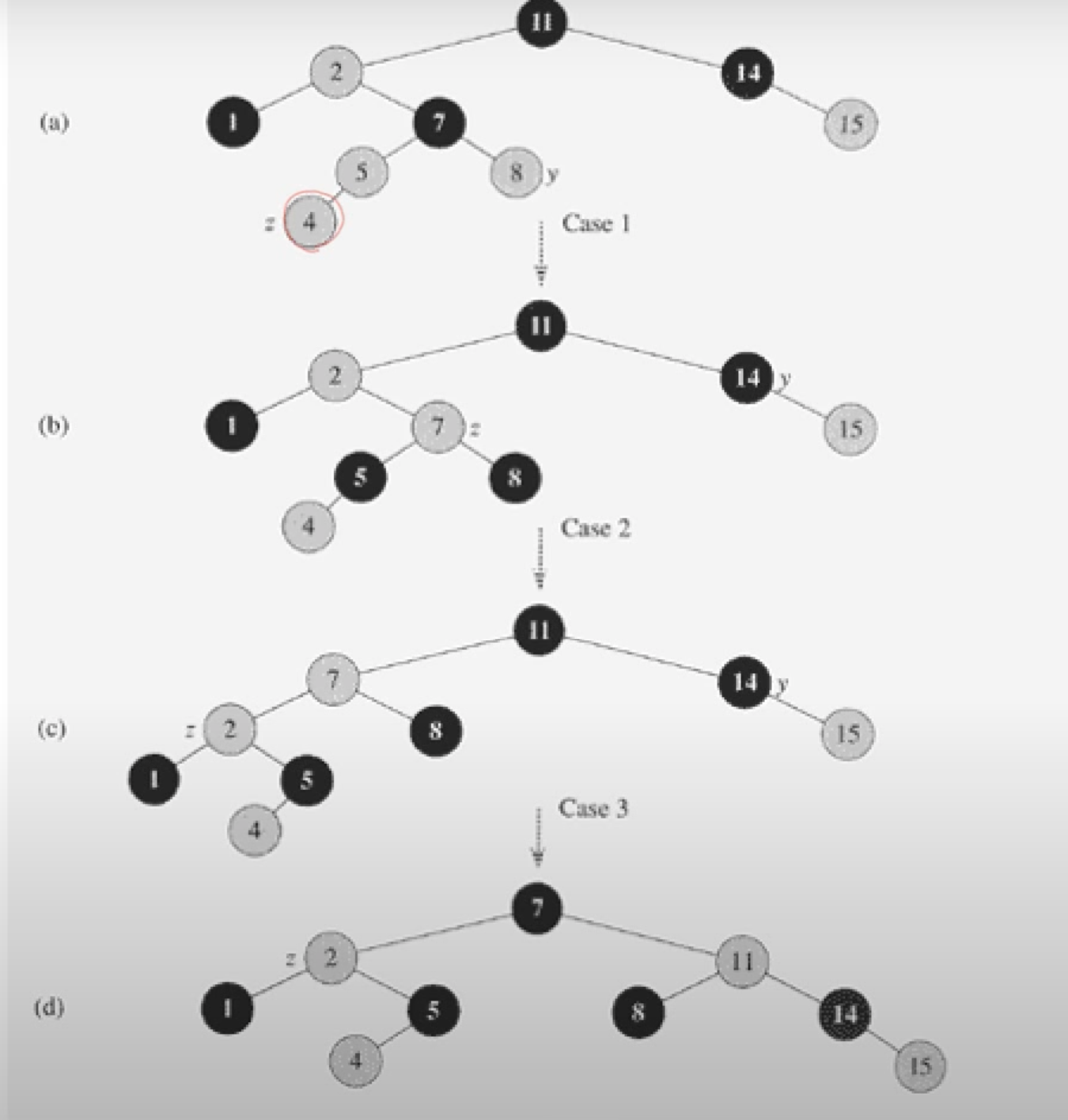
- 만약 z가 루트노드라면, color에서 red이므로 위반. -> 루트를 black으로 전환
- z의 부모, parent[z]가 red라면, red가 연속되어서 위반. -> z의 부모노드가 black이 되면 종료.
z의 할아버지노드는 늘 존재할까?
늘 존재한다. 왜냐하면, z의 부모노드가 red이므로, root노드가 아니기때문!
그렇기때문에, z의 할아버지노드가 있다는 가정하에 RB-Insert-Fixup을 만든다.
고려해야할 케이스
고려해야할 케이스는 총 6가지이다.
z노드가 z노드의 할아버지 노드의 왼쪽에 위치한노드일때, 3가지
z노드가 z노드의 할아버지 노드의 오른쪽에 위치한노드일때, 3가지
따라서, 1,2,3의 케이스는 4,5,6의 케이스와 대칭관계이다.- CASE1: z의 삼촌이 red
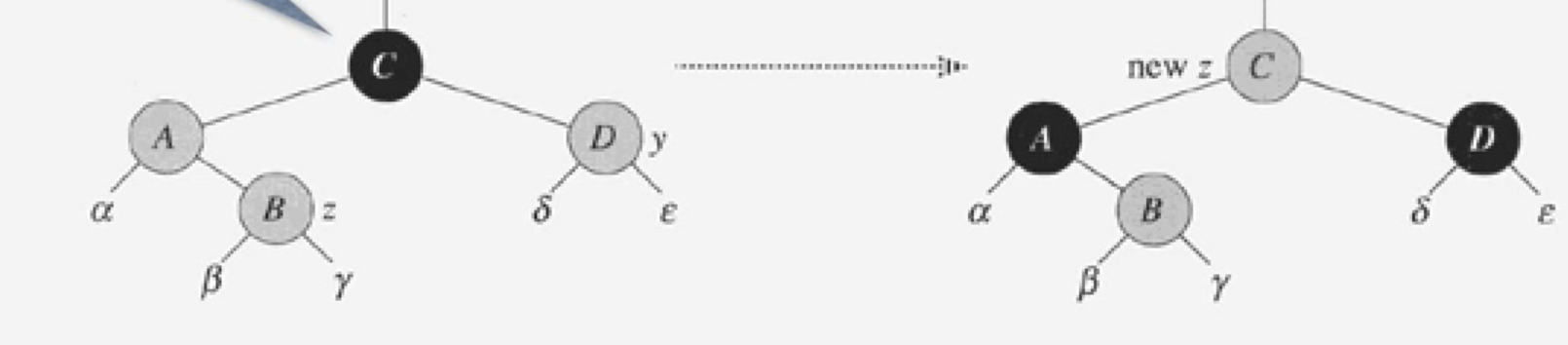
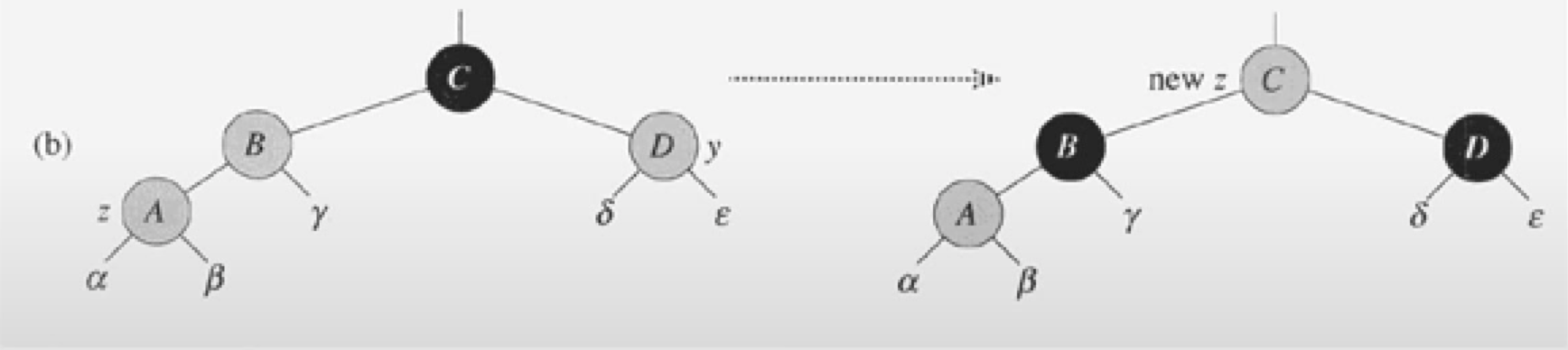
- 부모와 삼촌의 노드를 black으로 바꿔준다.
- 할아버지노드를 red로 바꿔준다.
- 만약, 할아버지의 부모노드가 red라면, red가 연속되므로 노드를 따라올라가면서, 수정을 해준다. -> CASE2 or CASE3
- CASE2 : z의 삼촌이 black, z가 오른쪽 자식인경우
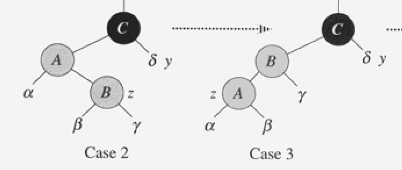
- parent[z]에 대해서 left-rotate을 한후에, p[z]를 z로!
- CASE3로!
- CASE3 : z의 삼촌이 black, z가 왼쪽 자식인 경우
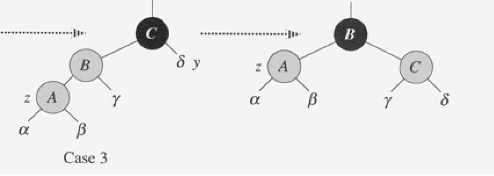
- parent[z]를 black, parent[ parent[z] ]를 red로 바꾼다.
- parent[ parent[z] ]에 대해서 right-rotate
RB_Insert-Fixup(T, z)
{
while (parent[z] && color[ parent[z] ] == RED) // 부모와 자식이 red로 연속되는동안
{
if (parent[z] == left[ parent[ parent[z] ] ])// 할버지노드의 왼쪽일때
{
y = right[ parent[ parent[z] ] ]; // y는 z의 삼촌노드
if (color[y] == RED) // CASE1 : 삼촌노드가 red인경우
{
// z도 red, z의 부모도 red, 삼촌노드도 red, 할아버지노드는 black
color[ parent[z] ] = BLACK;
color[y] = BLACK;
color[ parent[ parent[z] ] = RED;
}
else // CASE2, CASE3: 삼촌노드가 black인 경우
{
// CASE2 : z가 부모의 오른쪽 자식일때
if (z == right[ parent[z] ])
{
z = parent[z];
Left_Rotate(T, z);
}
// CASE3 : z가 부모의 왼쪽 자식일때
color[ parent[z] ] = BLACK;
color[ parent[ parent[z] ] ] = RED;
Right_Rotate(T, parent[ parent[z] ]);
}
}
else
// 대칭으로, CASE4, CASE5, CASE6의 경우
}
// CASE1을 반복하다가 빠져나온 경우를 고려
// 루트가 red인 경우를 고려
color[ root[T] ] = BLACK;
}
Delete
보통 BST에서 처럼 delete를 한다.
실제로 삭제된 노드 y가 red였으면 종료.
y가 black이었을경우, RB_Delete_Fixup호출
RB_Delete(T, z)
{
// z의 자식이없거나, 1개일때
if (left[z] == NIL[T] || right[z] == NIL[T])
y = z;
else // z의 자식이 2개일때
y = Tree_Successor(z); // 무조건 최대 자식이 1
// x는 y의 자식노드
if (left[y] != NIL[T])
x = left[y];
else
x = right[y];
// 부모연결
parent[x] = parent[y];
// y가 root일때
if (parent[y] == NIL[T])
root[T] = x;
else if (y == left[ parent[x] ])
left[ parent[y] ] = x;
else
right[ parent[y] ] = x;
// z의 successor를 삭제한 경우
if (y != z)
key[z] = key[y]; // 데이터 카피
// 삭제했던 노드가 black이었다면!
if (color[y] == BLACK)
RB_Delete_Fixup(T, x);
return y;
}
RB_Delete_Fixup
위의 delete함수에서 RB-Delete-Fixup이 나오기전까지
이진탐색트리의 delete와 같다.
하지만 그대로 끝낸다면, 위반될수있는 조건들이 있다.
RB_Delte_Fixup에서의 인자는 z가 아닌 x이다.
시간복잡도: O(logn)위반될수있는 조건들
- y가 root였고, x가 red인 경우 위반 -> 루트를 black으로 전환
- parent[y]와 x가 모두 red인 경우 -> x를 black으로 전환
- y가 black이었던 경우에는, black hight의 조건을 만족하지못함.
-> 1. 노드 x에 extra black을 부여해서 조건 5를 만족시킨다.
2. 노드 x는 double black 혹은 red & black
고려해야할 케이스
고려해야할 케이스는 총 8가지이다.
x노드가 부모의 왼쪽자식일 경우 4가지
x노드가 부모의 오른쪽자식일 경우 4가지
따라서, 1,2,3,4의 케이스는 5,6,7,8의 케이스와 대칭관계이다.- CASE1 : x의 형제노드가(w)가 red인 경우
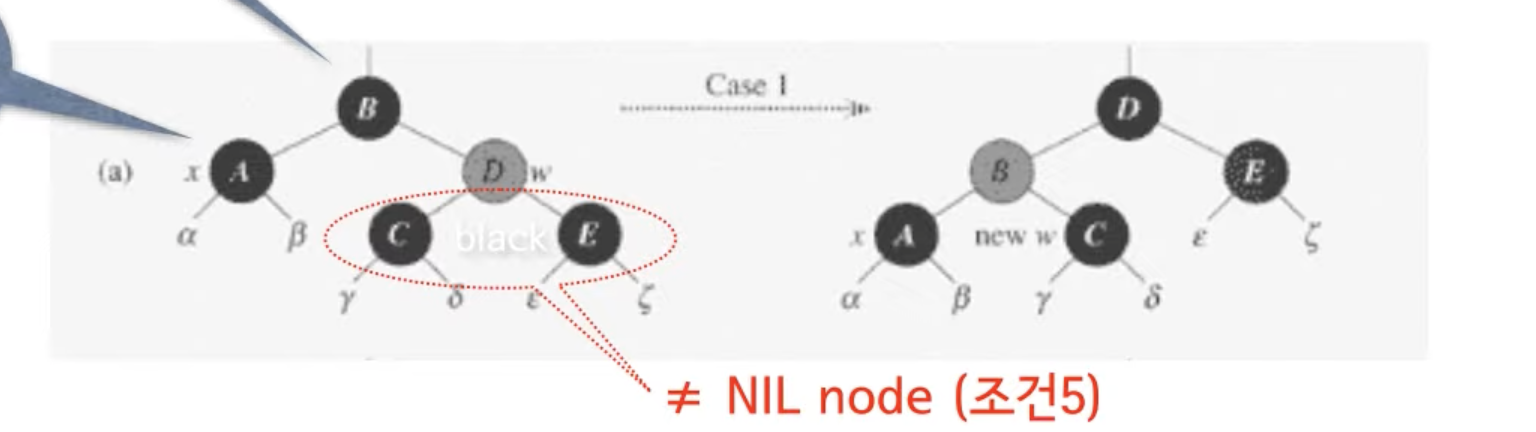
- w의 자식들은 모두 black, 또한 BH의 이유로 w가 NIL노드일수없다. (w가 red이기때문)
- x는 NIL 또는 double black이다.
- x는 double black이므로, C와 E는 NIL노드가 아니다. (루트로부터 NIL까지 같은 수의 블랙노드를 가져야하기때문)
- parent[x], 즉 B에대해서 left_rotate를 한다. (B와 D의 색상도 바꾼다)
- x는 아직 double black노드 이다.
- (이제 CASE2, 3, 4에 해당)
- CASE2 : w는 black, w의 자식들도 black
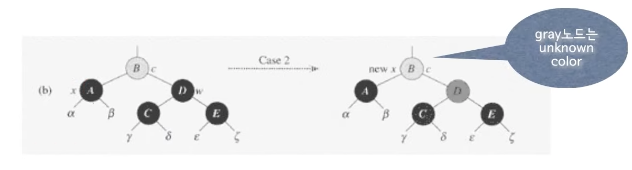
- x의 double black과, x의형제노드인 w의 black을 하나씩 빼서, 부모노드인 B에 준다.
- B가 red였다면, black이 되고, black이었다면, double black노드가된다.
- B의 노드에서 부모노드로 올라가면서 red인 노드를만나, black으로 바꿔준다.
- CASE3 : w는 black, w의 왼쪽자식이 red
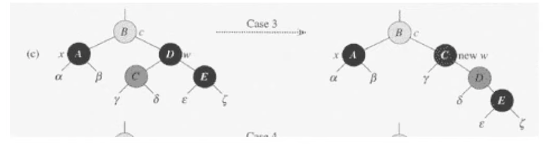
- w를 red로, w의 왼쪽자식을 black으로 바꾼다.
- w에 대해서 right-rotate를 적용.
- x의 새로운 형제노드 w는 이제 오른쪽자식이 red노드가된다.
- CASE4에 해당
- CASE4 : w는 black, w의 오른쪽자식이 red, 왼쪽자식은 red or black
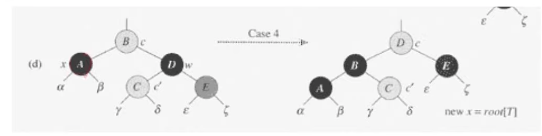
- w의 색을 현재 parent[x]의 색으로 변환.
- parent[x]를 black으로, w의 오른쪽자식을 black으로.
- parent[x]에 대해서, left-rotate 적용. (A가 가지고있는 double black을 B와 나눈다. 그 결과, 왼쪽 오른쪽 모두 NIL까지의 black노드의 수를 유지할수있다)
- x의 extra-black을 제거하고 종료.
CASE1 -> CASE2, CASE3, CASE4 -> ...
CASE2 -> CASE2 반복 or -> CASE1, CASE2, CASE3, CASE4 -> ...
CASE3 -> CASE4 -> 종료
CASE4 -> 종료
// x는 원래삭제했던, y의 자식노드. y의 자리를 차지하고있는 노드
RB_Delete_Fixup(T, x)
{
// x가 red라면, black으로 변환후 종료
while (x != root[T] && color[x] == BLACK)
{
if (x == left[ parent[x] ])
{
// w는 x의 형제노드
w = rignt[ parent[x] ];
// CASE1
if (color[w] == RED)
{
color[w] = BLACK;
Left_Rotate[T, p[x]];
w = right[ parent[x] ];
}
// CASE2, w의 자식이 둘다 black노드인 경우
if (color[ left[w] ] == BLACK && color[ right[w] ] == BLACK)
{
color[w] = RED;
x = parent[x];
} // CASE3, CASE4
else
{
// CASE3, w의 오른쪽자식이 black인 경우, x는 doule black상태
if (color[ right[w] ] == BLACK)
{
color[ left[w] ] = BLACK;
color[w] = RED;
Right_Rotate(T, w);
}
// CASE4 : x의 double black을 나눠준다.
color[w] = color[ parent[x] ];
color[ parent[x] ] = BLACK;
color[ right[w] ] = BLACK;
Left_Rotate(T, parent[x]);
// 해결후, while문을 빠져나가기위해서
x = root[T];
}
}
else if (x == right[ parent[x] ])
{
대칭적상황
}
}
color[x] = black;
}
