Jensen's Inequality proof

젠센의 부등식에 대해 한번 증명을 해보겠습니다. Ox edux에서 만든 영상을 이용하여 설명할 것입니다. 젠센의 부등식을 공부하는 목적은 VAE 또는 DDPM의 ELBO를 유도하는 과정이 Jensen’s Inequality(표준 변분 추론)를 이용하는 방식과 KL 발산의 비음수성(non-negativity) 두가지로 나뉘기 때문입니다.

젠센의 부등식은 임의의 확률변수 X와 볼록(convex) 함수 g에 대해 다음을 말합니다:

만약 g가 오목(concave) 함수라면 부등호 방향이 반대가 되어,

특히, 로그 함수는 오목 함수이므로,

이를 Diffusion Model 등에서 변분 추론을 할 때 자주 사용하는 꼴로 나타내면,

여기서

$X = \dfrac{p_\theta(x_0, x_{1:T})}{q(x_{1:T}\mid x_0)}$,

$q(\cdot\mid x_0)$는 근사 posterior(또는 forward process) 분포를 의미합니다.

이제 두말 없이 증명을 해보겠습니다.

Ox educ에서 만든 증명 영상의 링크는 아래와 같습니다.

젠센 부등식 증명 영상

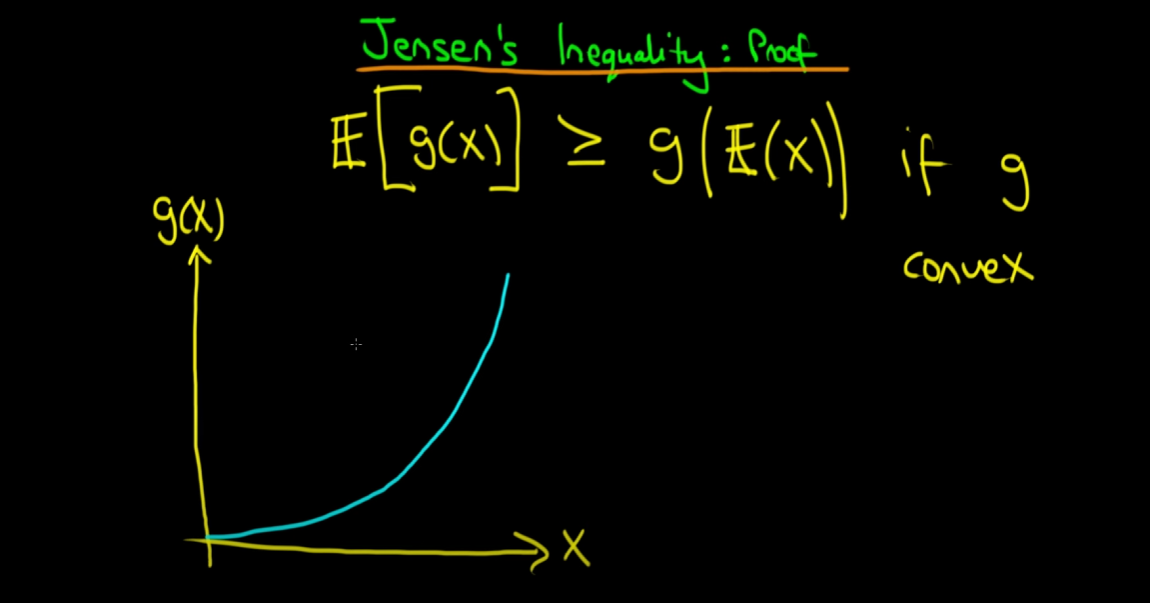
g(x)가 convex(볼록)할 때, 그래프를 그리면 위와 같이 파란색 곡선이 됩니다.

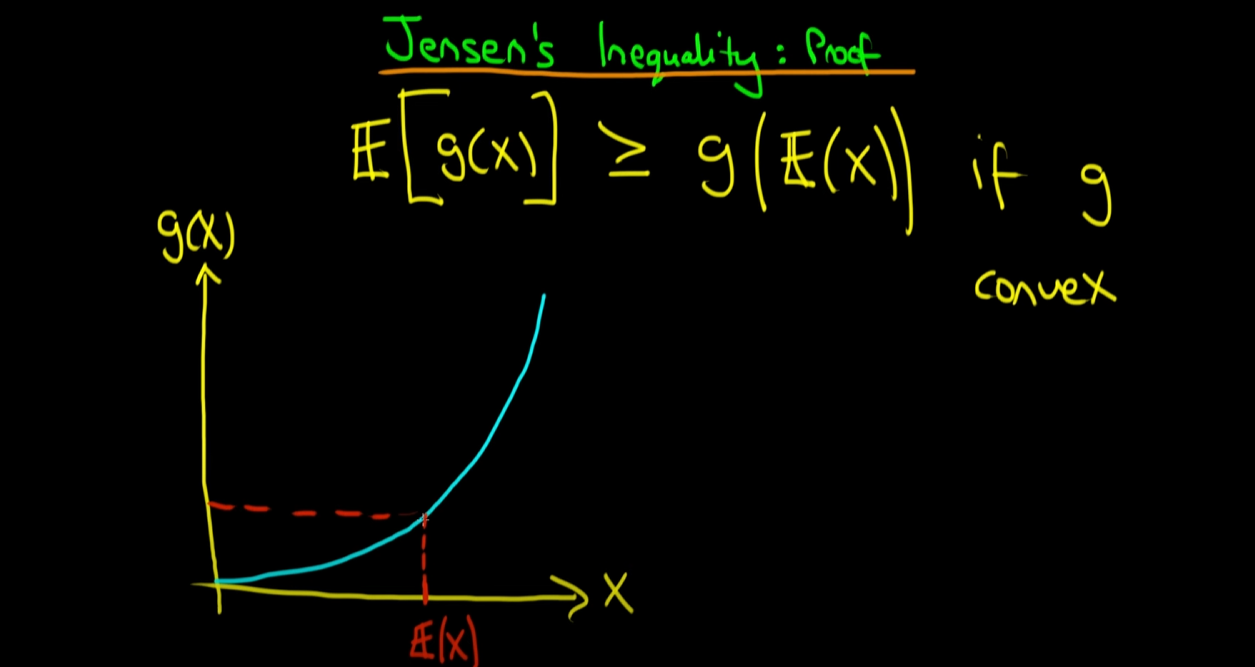
이제 x축 위에 E(x)라는 특정 지점을 표시하고 이를 g(x) 곡선과 매칭 시킵니다. 참고로 E(x)는 x라는 확률 변수의 기댓값이므로 스칼라 입니다. 그렇기에, 위의 그래프처럼 x축 중간 어딘가의 하나의 점으로 표현할 수 있습니다.

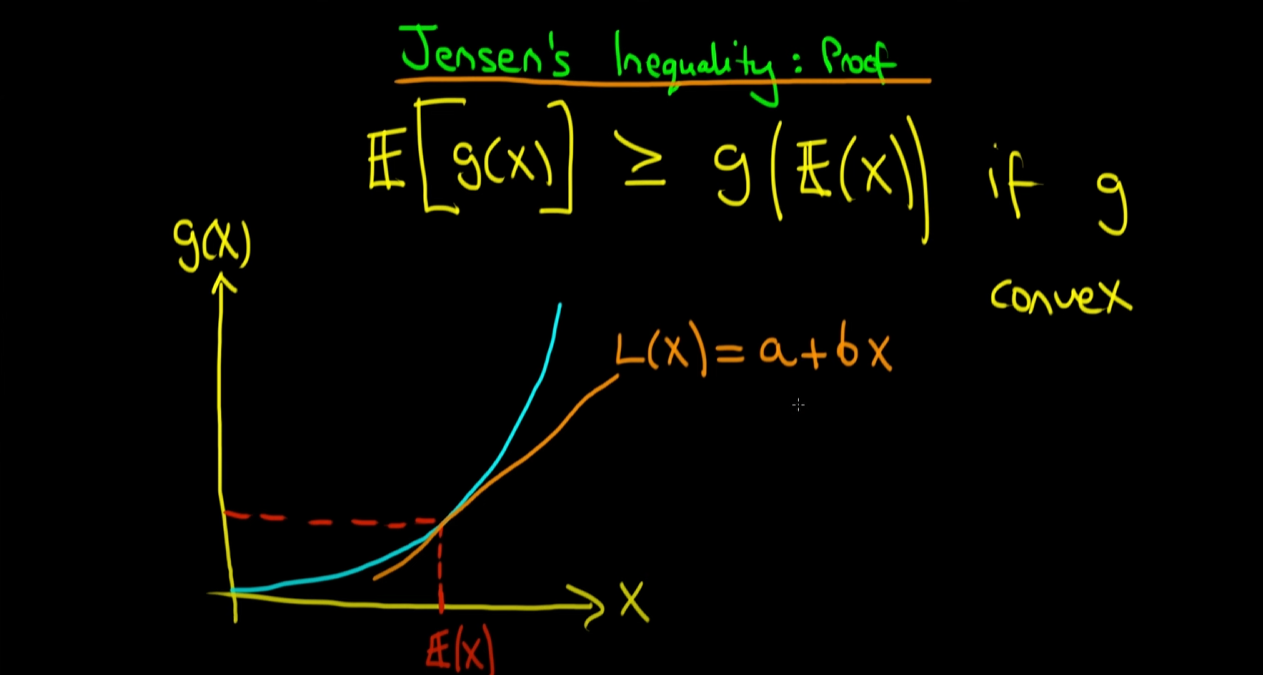
다음으로, g(x) 곡선 위의 점인 (E(x), g(E(x))를 접점으로 하는 접선을 그리고, 이를 L(x) = a + b(x)이라고 정의합니다. 직선은 일차식이기 때문에 a + bx로 표현하는 겁니다. a는 상수, b는 기울기라고 보면 됩니다.

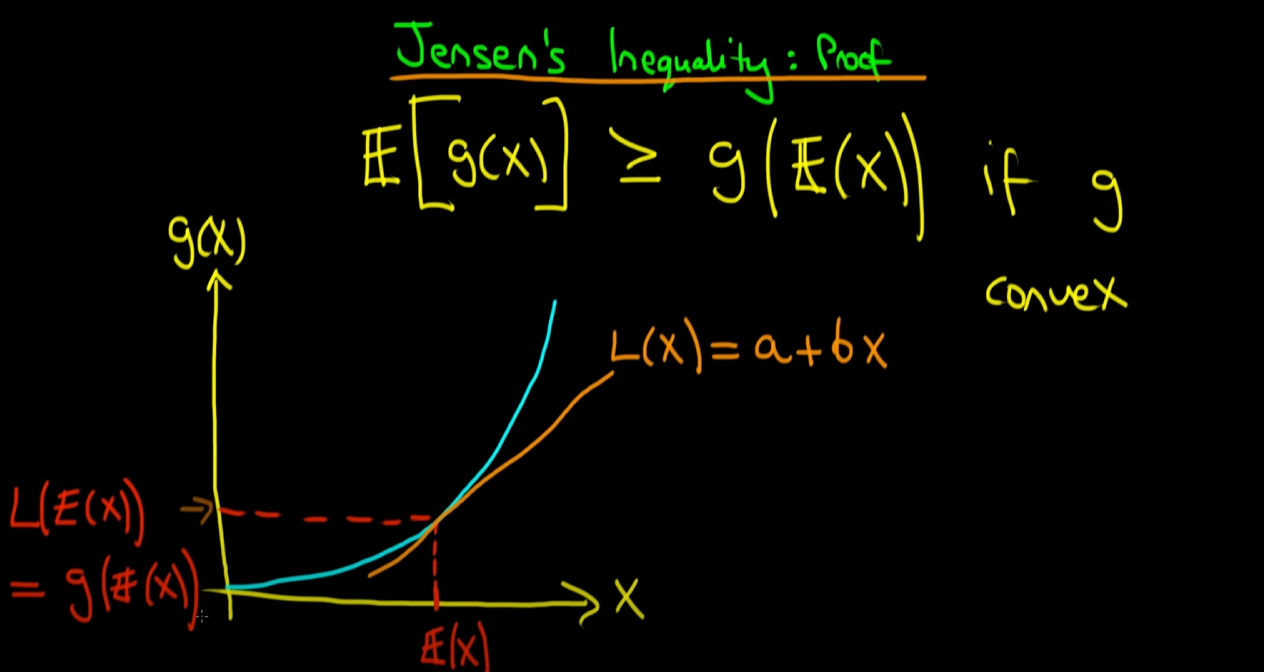
다음은 약간 중요한 부분입니다. (E(x), g(E(x))라는 점이 g(x) 곡선과 a + bx라는 직선 모두의 위에 있으므로, L(E(x)) = g(E(x)) 가 성립되게 됩니다. 이 수식은 나중에 쓰이게 되므로 이를 (가)라고 지칭 하겠습니다.

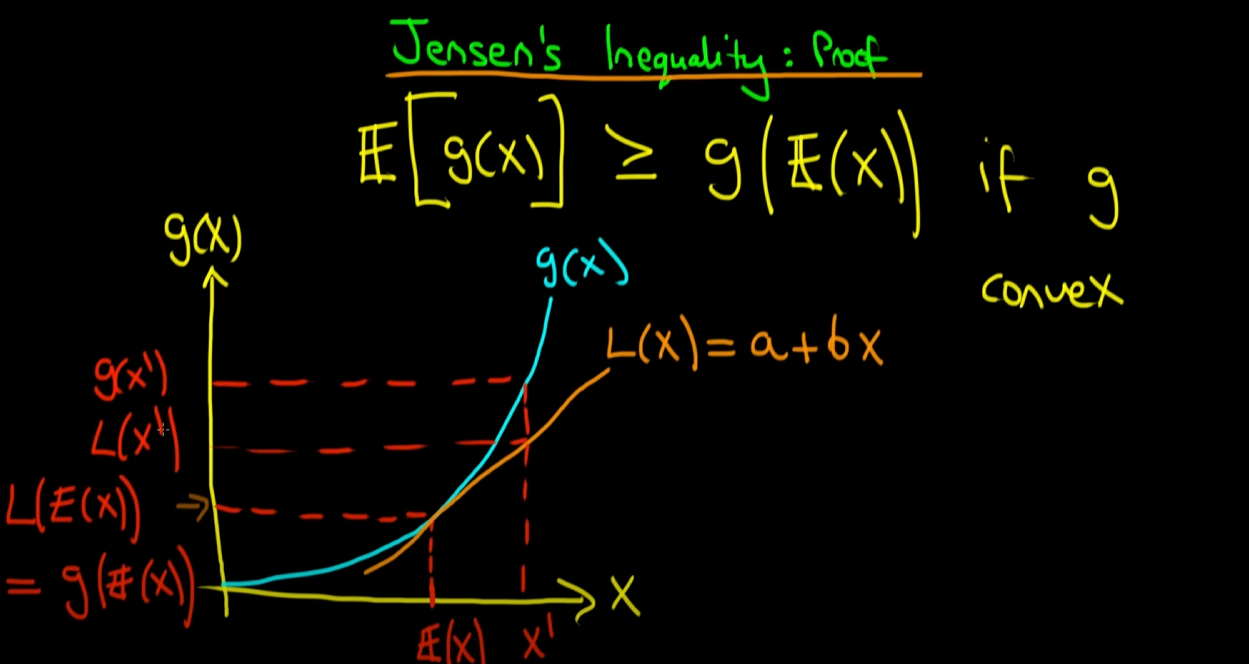
다음은 x $\neq$ E(x)가 아닌 x' 이라는 특정 점에 대해서 각 함숫값들이 어떻게 나타나는지를 보여주는 부분입니다. 위의 그래프에서 볼 수 있듯이 어떤 x'에 대해서도 g(x') $\geq$ L(x')가 됩니다.

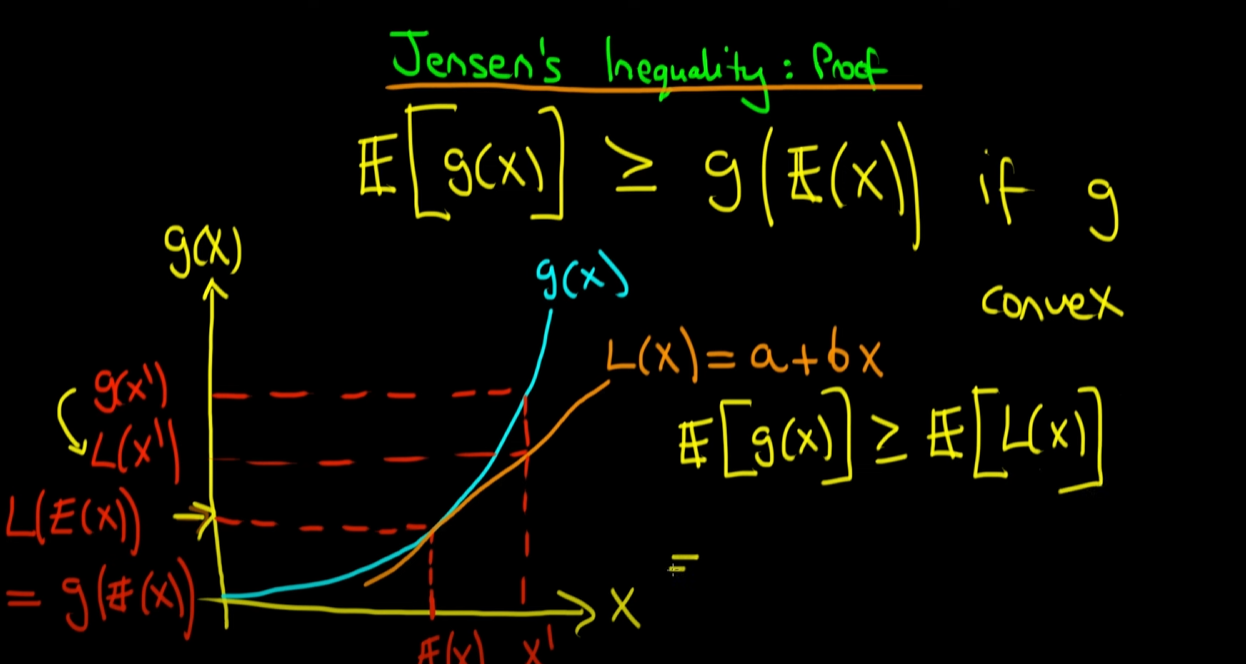
앞서 필요한 수식에 대해서 다뤘었습니다. 이제 젠센 부등식을 증명하겠습니다. g(x)의 기댓값인 $\mathbb{E}\bigl[g(X)\bigr]$은 $\mathbb{E}\bigl[L(X)\bigr]$보다 항상 크거나 같게 됩니다. 왜냐하면, 위에서 설명했듯이 X = E(x) 일때나, X $\neq$ E(x)인 모든 점에 대해서 함숫값 g(x)가 L(x)보다 크거나 같기 때문에 이를 평균내는 기댓값에서도 당연히 $\mathbb{E}\bigl[g(X)\bigr]$가 $\mathbb{E}\bigl[L(X)\bigr]$보다 크거나 같아 지게 되는겁니다. (모든 점에 대해서 함숫값이 크거나 같으면 평균도 당연히 크거나 같을 수 밖에 없다.. )

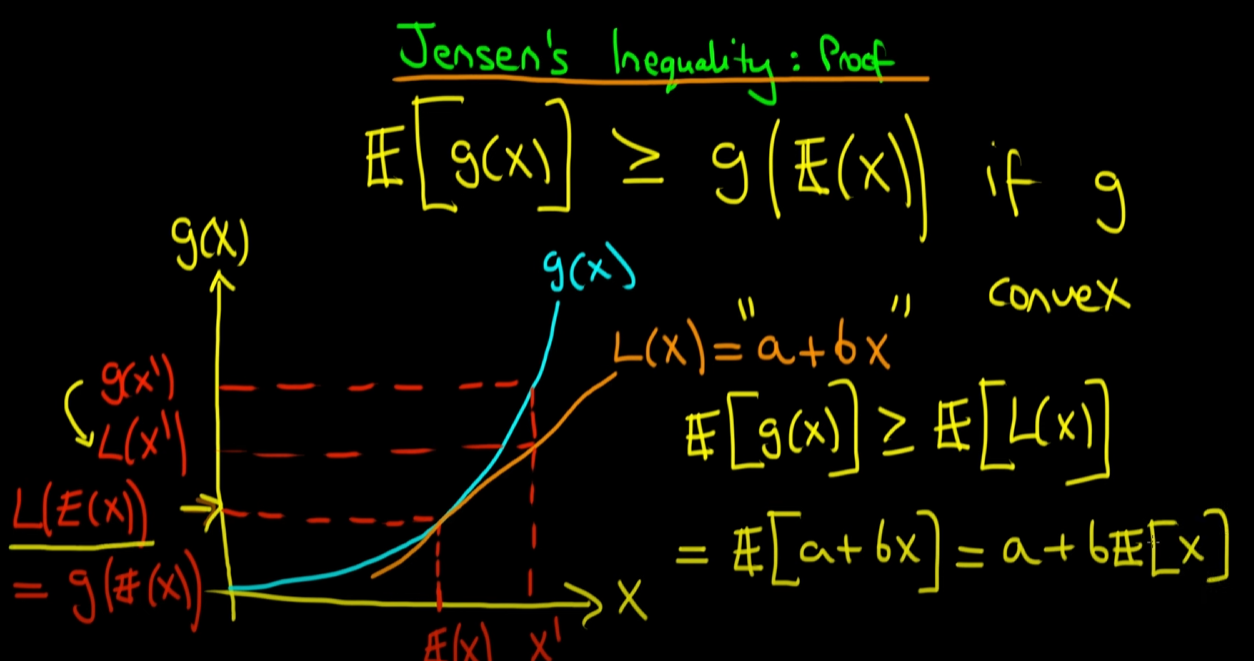
네 이제부터는 부등호의 우변인 $\mathbb{E}\bigl[L(X)\bigr]$를 계속해서 전개해보겠습니다. L(x) = a + bx이므로 이를 대입하면, $\mathbb{E}[a + bx]$가 되고 기댓값의 선형성 (linearlity)에 의해 a + b * $\mathbb{E}[x]$로 분리가 됩니다.

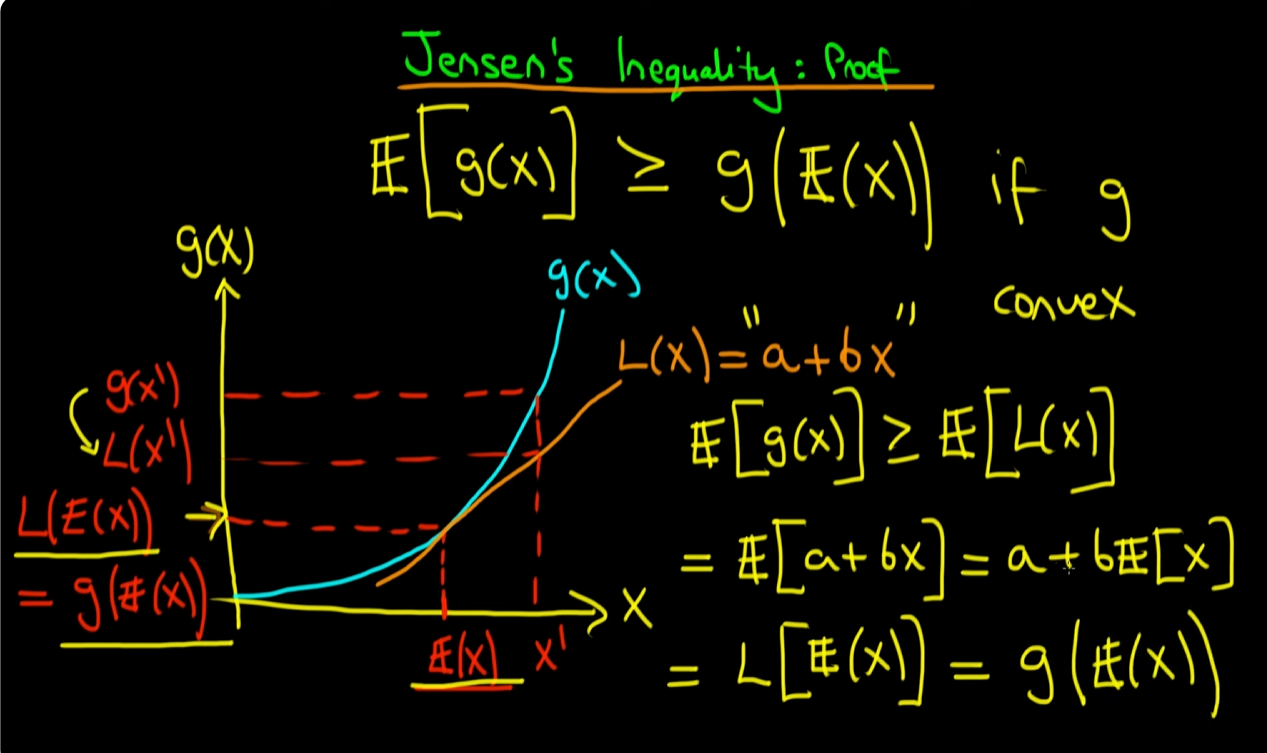
이제 마지막입니다. a + b * $\mathbb{E}[x]$는 L(x) = a + bx라는 직선에 x = E(x)를 대입한 형태이므로 L(E(x)) 형태로 다시 쓰게 됩니다. 그리고 이전에 제가 설명할 때, (가)라고 지칭해둔 부분이 있습니다. (가)에 의해 L(E(x))가 g(E(x))가 되면서 $\mathbb{E}\bigl[g(X)\bigr] \ge g\bigl(\mathbb{E}[X]\bigr)$가 성립되게 됩니다.

증명은 여기서 끝이고 다음 페이지에서는 Jensen’s Inequality(표준 변분 추론)를 이용하는 DDPM의 ELBO의 유도과정에 대해서 설명해보겠습니다.