K번째 수 : https://www.acmicpc.net/problem/1300
Problem
Solve
이분 탐색 알고리즘을 좀 풀어보고 싶어서 시도해봤는데, 이걸 어떻게 이분 탐색으로 풀지 라는 생각을 했었다.
이 문제를 이분 탐색으로 풀기 위해서는 몇가지 찾아내야하는 것이 있다.
A[i][j] = i*j로 배열을 초기화 한다면 n행을 n단으로 놓는 구구단이 된다. (3행 == 3단)B[k] = x는B배열의 k번째에는 x이다. 로 해석할 수 있다. 하지만 다르게 생각하면x와 같거나 작은 값이 k개가 있다.(B배열은 오름차순 정렬되어있음)
예를 들어 B = {1,2,2,4} 일 때 k=2이면 x=2를 찾아야한다. 그렇다는 것은 2보다 작거나 같은 값은 B배열에서 2개 (1,2)이다, k=3이면 4보다 작거나 같은 값이 3개 있다는 것으로 해석할 수 있다.
이게 왜 이분 탐색을 풀기 위해서 찾아야 하는 것인지는 설명하다보면 이해가 될 것이다.
문제에 주어진 예제에서 A배열과 B배열을 그림으로 나타내면 아래와 같다.
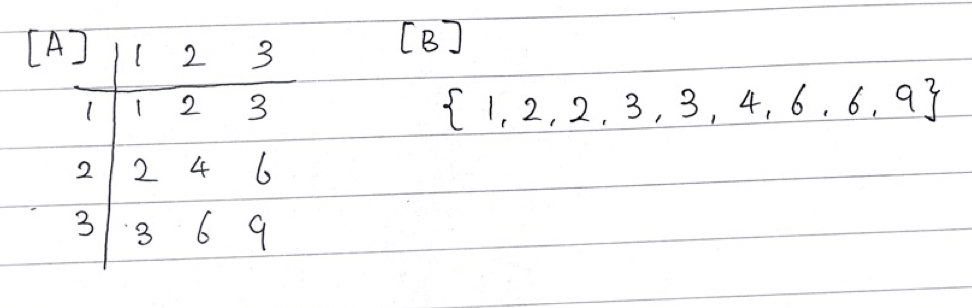
N = 3이고 K = 7인 경우 우리가 찾고자하는 값은 B배열의 7번째 값 6이다.

정렬된 배열에서 특정 값을 찾고자 한다.. 이분 탐색법을 공부할 때 배웠던 내용이다.
이분 탐색법을 사용하기 위해서는 탐색을 시작할 시작점과 끝점을 가지고 2분할로 나눠가며 탐색한다.
보통은 그렇지만 해당 문제에서는 배열의 위치가 아닌 값을 찾는것이다. 그렇기 때문에 시작점과 끝점을 배열이 모두 가질수 있는 값의 범위인 1~N*N으로 놓고 값을 탐색할 것이다.
그렇다면 값을 2분할로 나누는 기준는 무엇으로 할것인가?
바로 각 행이 가지는 임의의 값(mid)보다 작거나 같은 값의 누적값이다.
예를 들어 임의의 값을 6으로 놓았을때 1행은 3개, 2행은 3개, 3행은 2개를 가진다. 각 행의 값의 누적은 7개. 곧 임의의 값의 누적 갯수와 K값을 비교한다.
각 행이 가지는 임의의 값보다 작거나 같은 값의 누적 갯수는 임의의값 / 행이다.
그럼 이분 탐색법을 사용해 볼껀데 이분 탐색법에서도 Lower Bound 알고리즘을 사용했다.
...
long front = 1;
long rear = (long)N*N;
long mid;
while(front < end){
mid = (front+rear)/2;
long count=0;
//임의 값보다 작거나 같은 수의 누적 갯수
for(int i=1;i<=N;i++){
count += Math.min(N, mid/i);
}
//임의의 값의 누적 갯수가 K보다 작다면 탐색범위를 더 높은 갯수인 임의 값을 찾기 위해 front 증가
if(count<K){
front = mid+1;
}
//임의의 값의 누적 갯수가 K보다 크다면 탐색범위를 좁혀준다.
else{
rear = mid;
}
}
...여기서 임의의 값의 누적 갯수를 구할때 Math.min(N, mid/i)를 사용했는데 그 이유는 각 행에서의 최대 갯수는 N개이다. 하지만 임의의 값이 가질수 있는 최대 값은 N*N으로 count에 추가될수 있는 값은 최대가 N이므로 mid/i가 N보다 큰 값을 반환하게 되면 N을 계산에 사용할수 있도록 처리한 것이다.
이렇게 Lower Bound를 이용한 rear의 값에는 찾고자 k위치의 값 x가 있다.
Code
public class K번째수 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
int K = Integer.parseInt(br.readLine());
long front = 1;
//N이 100000이기 때문에 long을 써주거나 구하고자 하는 수값은 K를 벗어나지 못하므로 K로 써준다.
long rear = (long)N *N;
long mid;
while(front<rear){
mid = (front+rear)/2;
long count=0;
//임의 값보다 작거나 같은 수의 누적 갯수
for(int i=1;i<=N;i++){
//N보다 큰 값을 찾고자 할때 1행과 같은 곳에서는 N보다 큰값을 가질수 없기 때문에 최대 N으로 설정
count += Math.min(N, mid/i);
}
//임의의 값의 누적 갯수가 K보다 작다면 탐색범위를 더 높은 갯수인 임의 값을 찾기 위해 front 증가
if(count<K){
front = mid+1;
}
//임의의 값의 누적 갯수가 K보다 크다면 탐색범위를 좁혀준다.
else{
rear = mid;
}
}
bw.write(String.valueOf(rear));
bw.flush();
bw.close();
}
}
