프로그래머스 - 미로탈출

leehyunjon·2022년 5월 4일

다익스트라 비트마스크 카카오 프로그래머스

Algorithm

목록 보기

22/162

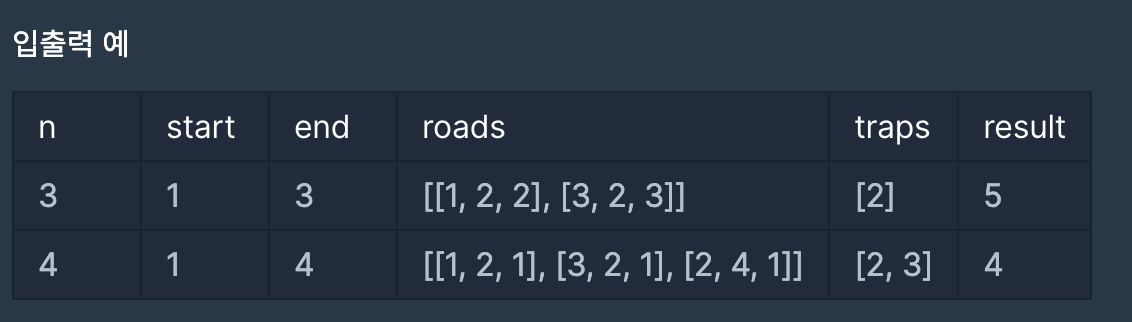
미로 탈출 : https://programmers.co.kr/learn/courses/30/lessons/81304

Problem

Solve

코테 준비한지 얼마 되지는 않았지만 가장 어려웠던 문제였던것 같다.
일단 비트 마스크도 몰랐어서 함께 공부했다.
비트 마스크는 딱 필요한 것만 정리해두고 자세한건 참고한 블로그에서 공부하자.
조회하려는 정수 N, 이벤트를 수행할 자리 i라고 할때

조회 : N &= 1 << i
추가 : N |= 1 << i
삭제 : N &= ~(1 << i)

그럼 풀이를 보자

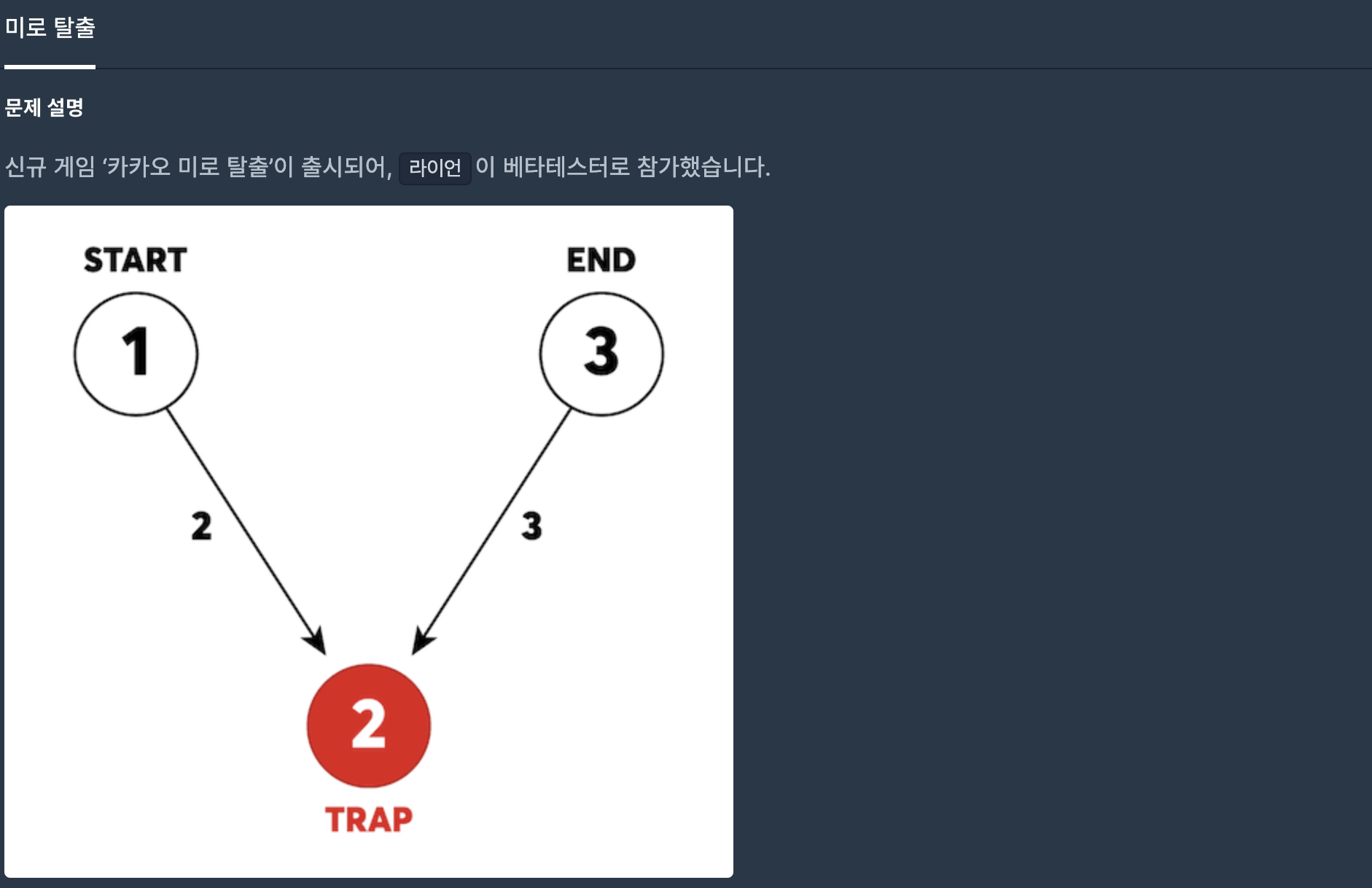
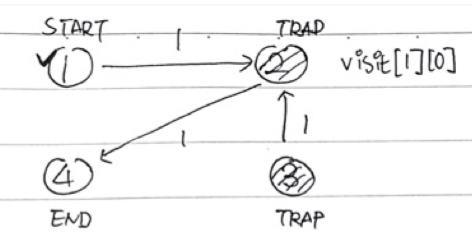
start = 1, end = 4, traps = {2,3}이라고 할 때 graph는 위의 그림과 같게 된다.

그리고 graph의 시작점에서 어느 지점까지의 최단 비용(시간)을 구하는 문제이니 다익스트라로 풀면된다.

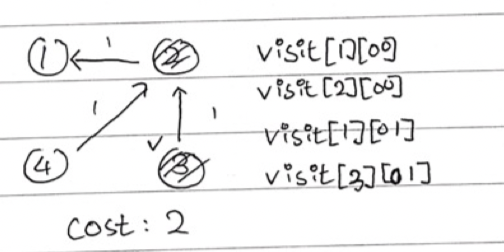
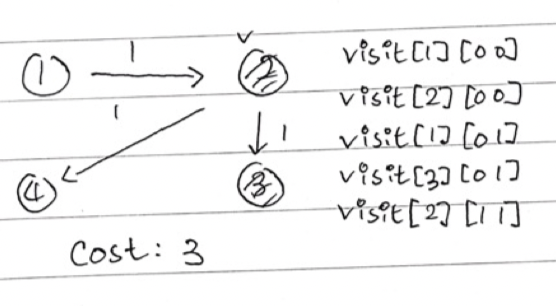
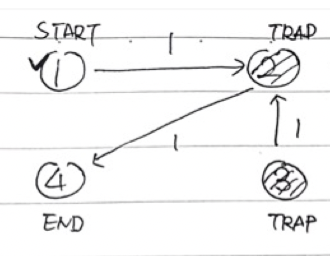
위 그림은 최단 비용을 구하는 것을 다익스트라로 구현하는걸 나타낸 것이다.

여기서 visit를 기존 다익스트라와 다르게 1차원 배열이 아닌 2차원 배열 visit[노드][상태]로 나타 내준다. 상태를 사용하는 이유는 trap노드가 활성화 되어있는지 아닌지 확인해야하는데 정수값으로 나타내기에는 너무 복잡하기 때문에 bit를 사용해서 최대 2^10의 경우까지 나타내는 것이다.

Code

import java.util.*;
class Solution {
    int[][] graph;
    int INF = 100000000;
    public int solution(int n, int start, int end, int[][] roads, int[] traps) {
        graph = new int[n+1][n+1];
        for(int i=0;i<=n;i++){
            for(int j=0;j<=n;j++){
                if(i==j){
                    graph[i][j] = 0;
                }else{
                    graph[i][j] = INF;
                }
            }
        }
        for(int[] road : roads){
            int p = road[0];
            int q = road[1];
            int s = road[2];
            //문제 조건에서 서로 다른 두 방 사이에 직접 연결된 길이 여러개 존재할수 있다고 했고 
            //최단 거리를 구하는 문제이기 때문에 주어지는 비용 중 가장 작은 값만 저장되면 된다.
            if(s < graph[p][q]){
                graph[p][q] = s;   
            }
        }
        
        
        return dijkstra(n, start, end, traps);
    }
    
    int dijkstra(int n, int start, int end, int[] traps){
    	//노드의 비용이 가장 작은 순으로 오름차순 정렬되는 PQ
        PriorityQueue<Node> pq = new PriorityQueue<>();
        pq.add(new Node(start, 0, 0));
        //노드의 상태의 최대 경우의 수는 2^10
        boolean[][] visit = new boolean[n+1][1<<10];
        
        while(!pq.isEmpty()){
            Node current = pq.poll();
            
            //방문했던 노드라면 무시
            if(visit[current.node][current.state]) continue;
            //현재 노드가 end값이라면 현재 노드의 비용 반환(최소 비용)
            if(current.node == end) return current.cost;
            visit[current.node][current.state] = true;
            
            //현재 노드의 trap여부와 다음 이동할 노드의 trap여부에 따라 서로 연결된 길의 방향이 달라지기 때문에
            //currentTrapped와 nextTrapped 선언
            //현재 노드의 trap여부
            boolean currentTrapped = false;
            //활성화 되어있는 trap
            HashMap<Integer, Boolean> trapped = new HashMap<>();

            for(int t = 0;t<traps.length;t++){
            	//현재 trap 노드의 state상의 위치
                int bit = 1<<t;
                //현재 노드의 상태가 해당 trap이 활성화 중
                if((current.state & bit)!=0){
                	//현재 노드가 해당 trap을 방문했다
                    if(current.node == traps[t]){
                    	//trap의 재방문은 trap 비활성화
                        current.state &= ~bit;
                    }
                    //활성화된 trap 저장
                    else{
                        trapped.put(traps[t],true);
                    }
                }
                //현재 노드의 상태가 해당 trap이 비활성화 중
                else{
                	//현재 노드가 trap을 방문
                    if(current.node == traps[t]){
                    	//현재 노드는 trap
                        currentTrapped = true;
                        trapped.put(traps[t],true);
                        //현재 상태에 해당 trap 활성화
                        current.state |= bit;
                    }
                }
            }
            
            //현재 노드와 인접한 노드를 찾는다
            for(int v=1;v<=n;v++){
                //다음 이동할 노드가 trap이 활성화된 노드인지
                boolean nextTrapped = trapped.containsKey(v);
                //다음 노드와 현재 노드의 trap여부가 동일하다
                //(둘다 trap이 활성화 되어있거나, 활성화 되어있지 않으면 방향 변화 x)
                if(nextTrapped == currentTrapped){
                	//방향이 바뀌지 않음으로 인접노드인 경우 pq에 추가
                    if(graph[current.node][v]!=0){
                        pq.add(new Node(v,current.cost+graph[current.node][v], current.state));
                    }
                }
                //다음 노드와 현재 노드의 trap여부가 동일하지 않다.
                //(둘중 하나만 trap이 활성화 되어있다면 방향 변경)
                else{
                	//방향이 바뀌어 x,y를 바꿔 참조
                    if(graph[v][current.node] != 0){
                        pq.add(new Node(v,current.cost+graph[v][current.node], current.state));
                    }
                }
            }
        }
        
        //미로를 탈출할수 있는 경우만 주어진다고 했지만 임의의 결과값.(의미없음)
        return INF;
    }
    
    class Node implements Comparable<Node>{
        int node;
        int cost;
        int state;
        public Node(int node, int cost, int state){
            this.node = node;
            this.cost = cost;
            this.state = state;
        }
        
        @Override
        public int compareTo(Node o){
            return this.cost-o.cost;
        }
    }
}