Problem
N의 크기의 배열에 각 a와 b 인덱스 사이에 k의 값을 추가해주고, 겹쳐지는 구간은 k를 다른 k와 합하여 줍니다.
모든 작업을 수행하였다면 모든 구간에서 가장 큰 값을 반환해야합니다.
N = 10
qureis = [[1,5,3],[4,8,7],[6,9,1]]
이 주어졌을때 아래와 같습니다.
a b k
1 5 3
4 8 7
6 9 1그리고 각 a와 b사이에 k를 N크기의 배열에 작업을 수행한다면 아래와 같이 됩니다.
index-> 1 2 3 4 5 6 7 8 9 10
[0,0,0, 0, 0,0,0,0,0, 0]
[3,3,3, 3, 3,0,0,0,0, 0]
[3,3,3,10,10,7,7,7,0, 0]
[3,3,3,10,10,8,8,8,1, 0]조건
3 <= N <= 10^7
1 <= M(quries.size()) <= 2*10^5
1 <= a <= b <= N
0 <= k <= 10^9
Solve
영어 문제는 이해하는게 참 어려운것 같습니다.
첫번째 풀이에서는 단순 구현을 통해 모든 a와 b 구간에 k를 더하여주었습니다.
조건을 보니 O(NM)으로 시간초과가 발생하였습니다.
M은 필수적으로 발생하므로 a와 b구간에 k를 더해주는 것을 O(1)이나 O(logN)으로 줄여줘야 했습니다.
누적합을 통해 구간의 합을 구해줄 수 있습니다.
a~b까지 k를 모두 더해주는 것이아닌, a와 b+1 구간에만 k의 추가와 삭제를 표시해주면 O(N)으로 구간에서 최대값을 구할 수 있습니다.
N = 5, M = 3
quries = [[1,2,100],[2,5,100],[3,4,100]]
일 때,
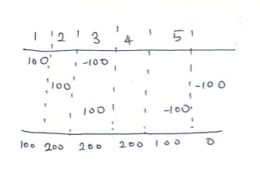
arr[1]에 100, arr[2+1]에 -100
arr[2]에 100, arr[5+1]에 -100
arr[3]에 100, arr[4+1]에 -100
을 저장해줍니다. 결과는 아래와 같습니다.
이해가 되지 않는다면, 각 a와 b구간에 k를 모두 적용하였을때는 아래와 같습니다.
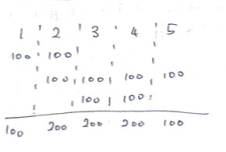
동일한 결과를 가지게 됩니다.
누적합을 구하였을때 1부터 5까지 누적합을 구해주고 그 과정에서 발생하는 최대값이 N범위에서 가지는 최대값이게 됩니다.
Code
class Result {
/*
* Complete the 'arrayManipulation' function below.
*
* The function is expected to return a LONG_INTEGER.
* The function accepts following parameters:
* 1. INTEGER n
* 2. 2D_INTEGER_ARRAY queries
*/
public static long arrayManipulation(int n, List<List<Integer>> queries) {
// Write your code here
long[] arr = new long[n+2];
long max = 0;
for(List<Integer> query : queries){
int a = query.get(0);
int b = query.get(1);
int k = query.get(2);
arr[a] += k;
arr[b+1] -= k;
}
long prefixSum = 0;
for(int i=1;i<=n;i++){
prefixSum += arr[i];
max = Math.max(max, prefixSum);
}
return max;
}
}