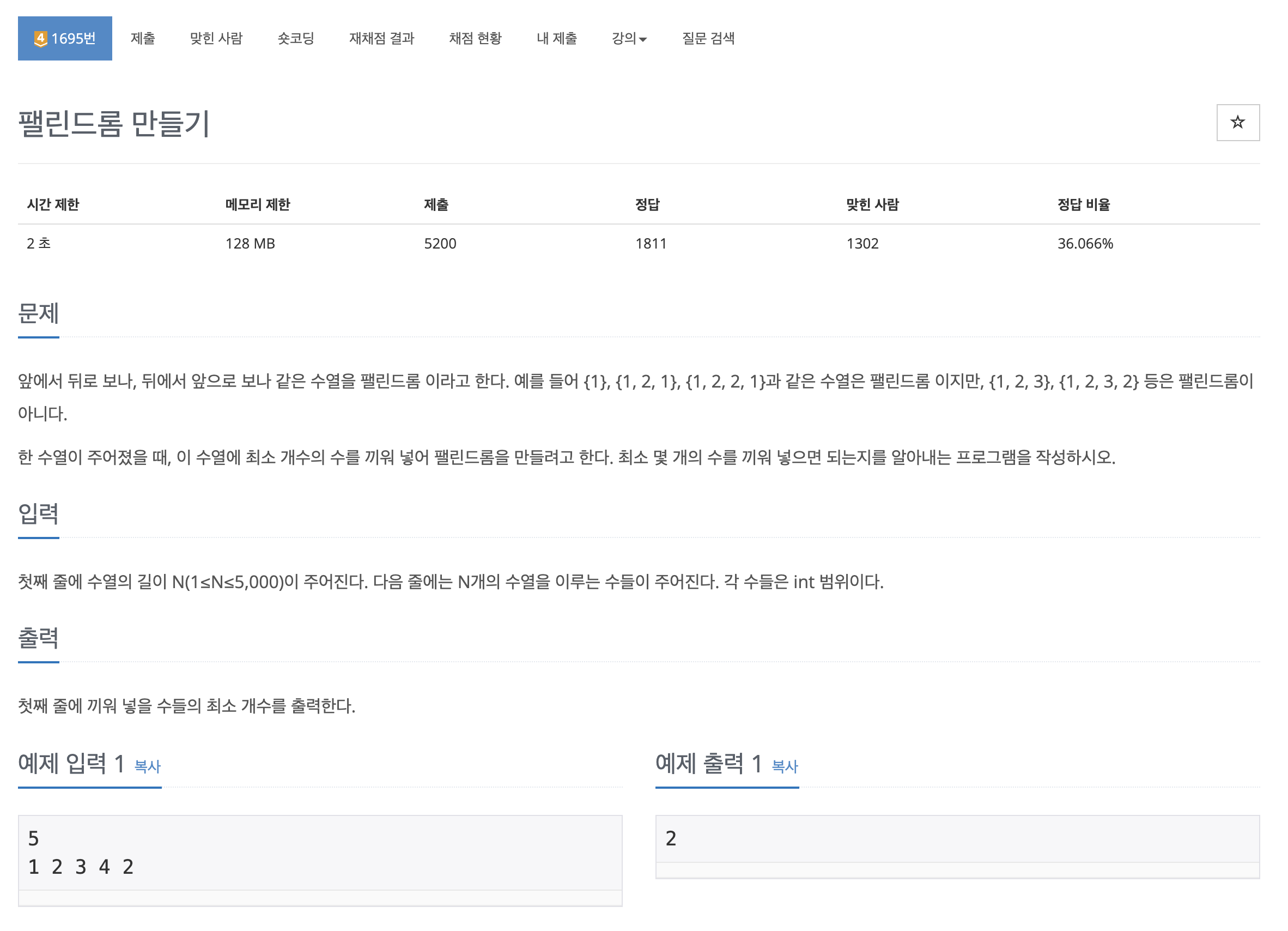
1695 팰린드롬 만들기 : https://www.acmicpc.net/problem/1695
Problem
Solve
접근 방법도 생각을 못했습니다.
DP로 풀수있다는 것에 신기했습니다.
주어진 수열에서 수를 끼워넣을 수 있는데, 끼워넣는 개수가 최소가 되어야합니다.
재귀를 통해 어떤 수를 끼워넣었을때 최소로 끼워넣을 수 있는 개수가 될까를 구합니다.
이 최소로 끼워넣을 수 있는 수의 개수를 DP에 저장해야합니다.
DP는 2차원 배열로 선언하고 DP[i][j]일 때 i와j에서 추가되는 최소 수를 저장해야합니다.
1 2 3 4 2의 수열이 주어졌다고 하겠습니다.

left를 0, right를 4로 초기화 하고 시작하겠습니다.
arr[0]의 1과 arr[4]의 2가 서로 다르기 때문에 팰린드롬으로 만들기 위해서는 둘 중 하나의 값을 끼워넣어주어야합니다.
먼저 1을 오른쪽에 추가해보겠습니다.

1을 추가했으니 left는 다음의 수를 가리킵니다.
그렇다면 arr[1]과 arr[4]는 둘다 2이기 때문에 팰린드롬 조건을 만족합니다. 그렇기 때문에 수를 끼워넣어줄 필요가 없으니 left, right둘다 한칸씩 이동합니다.
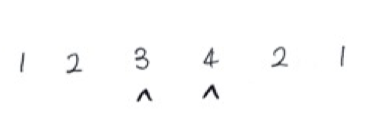
arr[2]의 3, arr[3]의 4는 서로 다른 값이기 때문에 팰린드롬 조건을 만족하기 위해 어떤 값을 끼워넣어주어야 합니다.
먼저 3을 오른쪽에 끼워넣어보겠습니다.

left와 right가 같은 값을 가리키게 되고, 값을 더이상 끼워넣을 필요가 없습니다.
그럼 이전으로 돌아가 4를 왼쪽에 끼워넣어보겠습니다.
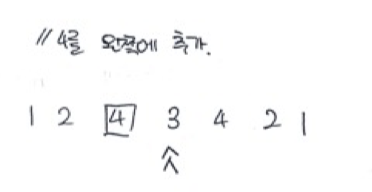
이 또한 같은 값을 가리키게 되고, 값을 더이상 끼워넣을 필요가 없습니다.
그럼 여기서, DP는 어디서 사용하느냐.
값을 끼워넣는 최소의 수를 DP에 저장해주어야합니다. 그렇기 때문에 더이상 수를 끼워넣을 필요가 없는 곳에는 수를 끼워넣는 최소의 수가 0이 됩니다. 즉, left, right가 동일한 곳을 가리키는 곳은 DP가 0이 끼워넣는 수의 최소가 됩니다.
left가 3, right가 3인 경우 DP[3][3]=0이 되는것입니다.
자 그렇다면, 4를 왼쪽에 추가해주었을때 left, right가 3을 가리키게 되었으니, 그 이전으로 돌아가자면 left가 3를 가리키고, right가 4를 가리키고 있을때, 4를 왼쪽에 추가했을때 최소 추가 수는 1, 3을 오른쪽에 추가했을때 최소 추가 수는 1이 되므로, DP[2][3] = 1이 됩니다.
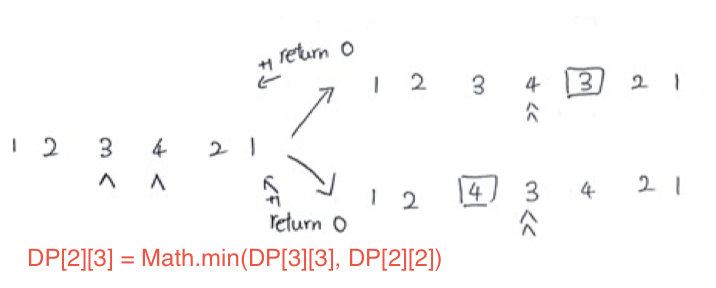
이런식으로 반복하면 DP[첫번째][마지막]에 수를 끼워넣어 팰린드롬을 만족하는 최소의 수가 저장되게 됩니다.
즉, DP[left][right]는 left가 가리키는 값을 오른쪽에 추가한 경우와 right가 가리키는 값을 왼쪽에 추가한 경우 중 적은 끼워넣은 수를 저장합니다.
DP[left][right] = Math.min(DP[left+1][right]+1, DP[left][right-1]+1)
이를 재귀에 적용한다면
public void recursive(int left, int right){
//left와 right가 같은 경우 return 0
//메모제이션 된 DP[left][right]는 압축
int min = 0;
//left와 right가 가리키는 값이 동일하다면 팰린드롬을 만족하므로 둘다 한칸씩 이동
if(arr[left] == arr[right]){
min = recursive(left+1, right-1);
}
//left와 right가 가리키는값이 다르다면 left가 가리키는 값을 오른쪽에 추가하는 경우와
//right가 왼쪽에 추가되는 경우를 비교하여 DP에 저장합니다.
else{
min = Math.min(recursive(left+1, right), recursive(left, right-1));
}
return DP[left][right] = min;
}Code
import java.io.*;
import java.util.StringTokenizer;
import java.util.Arrays;
public class Main{
static int[][] dp;
static int[] arr;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine()," ");
arr = new int[N];
for(int i=0;i<N;i++){
arr[i] = Integer.parseInt(st.nextToken());
}
dp = new int[N][N];
for(int i=0;i<N;i++){
Arrays.fill(dp[i],-1);
}
int min = putSequence(0, N-1);
bw.write(String.valueOf(min));
bw.flush();
bw.close();
}
static int putSequence(int left, int right){
if(left>=right) return 0;
if(dp[left][right]!=-1)return dp[left][right];
int min = 0;
if(arr[left]==arr[right]){
min = putSequence(left+1, right-1);
}else{
min = Math.min(putSequence(left+1,right)+1, putSequence(left,right-1)+1);
}
return dp[left][right] = min;
}
}Result
까도까도 신기한 DP
설명도 횡설수설해서 기억해두었다가 다시 풀어봐야할것같습니다.
